求解模型双击模型树上的,确保在机械设计工作台。把求解目录设置为文件所保存的目录。动画显示模型在求解完成后,可以动画显示模型。图23-20 运动图形窗口单击分析算题点选框,在右侧的模型树上选择。模拟的时间自动显示在x轴域内。在下面的列表Y轴域内,按下＜Ctrl＞键,选择和。从出现的菜单列表中选择2D绘制,然后单击下一步图标。单击完成按钮,显示新绘制的图形窗口,如图23-21所示。......
2025-09-29
天元术与分式方程：图解与求解
【摘要】：如图3.8.3①所示方程,则为x3 +336x2 +4184x+2488320 =0图3.8.3天元术而如图3.8.3②所示方程,则为此为《测圆海镜》第7 卷第2 题,该题给出5 种解法,列分式方程是其中一种方法。这种计数方法对于天元术是十分方便的,只需将分式方程中表示未知数一次项系数的“元”字向下移动两行即可,如图3.8.3③所示,方程则变为-x4 +8640x2 +652320x+4665600 =0一旦方程列出后,李冶再按增乘开方法求其正实根。
所谓天元术,就是一种用数学符号列方程的方法,“立天元一为某某”相当于今“设x 为某某”,但由于我国古代计算工具为算筹,故其写法有些不同。 我们现在是据已知条件列出两个相等的代数式,然后通过化简、合并同类项,得出等式一端为零的方程。 而按李冶的记法,因方程各项系数均为筹算数码,所以需在常数项旁记一“太”字(或在一次项旁记一“元”字),“太”或“元”向上每层增加一次幂,向下每层减少一次幂。
如图3.8.3①所示方程,则为
x3 +336x2 +4184x+2488320 =0
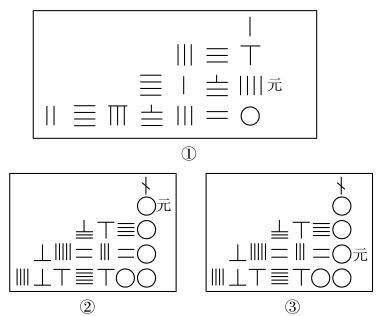
图3.8.3 天元术
而如图3.8.3②所示方程,则为(第一行算筹数码上的斜杠表示负数)(https://www.chuimin.cn)
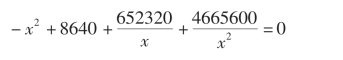
此为《测圆海镜》第7 卷第2 题,该题给出5 种解法,列分式方程是其中一种方法。 可知李冶已懂得用方程两边同乘一个整式的方法,把分式方程转化为整式方程。 这种计数方法对于天元术是十分方便的,只需将分式方程中表示未知数一次项系数的“元”字向下移动两行即可,如图3.8.3③所示,方程则变为
-x4 +8640x2 +652320x+4665600 =0
一旦方程列出后,李冶再按增乘开方法(我国古代求高次方程的一般方法)求其正实根。 资料表明,李冶所给化分式方程为整式方程的方法,超过了同期代数学较为发达的印度和阿拉伯的研究水平。
相关文章
- 详细阅读
-
建筑构图解析：立面与空间详细阅读
日本建筑师芦原义信用这句话表明了空间、建筑与人的关系。建筑空间设计的实质就是处理环境与环境、建筑与环境、建筑与建筑、人与建筑、人与环境之间的关系。而绝对分隔的建筑内部空间易给使用者带来压抑的心理感受，人长期处于压抑的心理状态会严重影响人的心理和生理健康。室外活动场所通常被作为过渡空间或缓冲空间联系建筑内外空间。......
2025-09-30
-
离间术揭秘：曾国藩识人术与用人之道详细阅读
在用人问题上，我们要警惕某些人因为种种原因而采取的离间术。离间术拂去圈套的伪装之后，实际上是一种主体对客体的侵害行为。离间术在生活中有多种表现，如创造条件，促使同志之间、上下级之间的误会；或将误会加以渲染，扩大他人之间的分歧；或编造谎言，制造矛盾，破坏他人团结，等等。离间术的外在表现虽然多种多样，但它的内在本质却是惟一的，那就是：使人为己，陷人益己，抑人扬己，损人利己。离间术有以下特征：目的性。......
2025-09-29
-
求解SAMCEF有限元分析与应用实例详细阅读
单击Check图标，如果出现No data incoherence detected，表明数据已经定义完整，不缺少数据。单击Close按钮返回。设置工作目录，浏览并选择目录E：\Work_Sam。设置求解需要的内存为200。Number Of Steps：输入10。Number of Eigen Values：输入特征值数4。单击图标，提交作业，并显示执行状态的监视对话框。当计算完成后，单击Close按钮，关闭监视对话框和Solver Launch对话框。单击工具条中的保存文件快捷图标保存文件。......
2025-09-30
-
建筑构图解析：形体、空间与构图详细阅读
2）当形态构成元素之间同时存在尺寸差异和位置差异时，尺寸差异决定元素间的主次关系，尺寸较大的是主要元素，成为构图中心。这两座建筑立面均采用中心轴对称的构图手法，左右两部分的尺寸与位置关系相同，建筑师通过对左右两部分构成元素复杂程度的差异化处理手法，使其产生主次对比关系，从而完善构图。......
2025-09-30
-
柱状线抽脚与缩头术的分析介绍详细阅读
第六节柱状线的抽脚与缩头在MACD指标图中，彩色的竖线是柱状线，一般用红线表示0轴上的部分，用绿线表示0轴下的部分，所以又被俗称为“红绿柱”，它表示DIF与DEA之间的差值，在指标图中表示DIF线与DEA线的距离之间的变化。柱状线的抽脚与缩头MACD柱状线的重要作用就是通过研究它的收敛和发散来找出市场变化的转折点，作为波段操作依据。当柱状线在0轴下，由绿柱不断接近0轴，最终出现红柱时，说明市场开始进入短期的多头。......
2025-09-29
-
控制方程求解的方法与优化详细阅读
式即为动态分析中实际求解的有限元代数方程组。由于式考虑了渗透张量与应力的耦合关系，即使采用弹性本构模型，式也是一个非线性方程组，仍需在每一个计算时步内迭代求解。当然与式相比，式消除了自由面边界非线性的影响，非线性仅来源于随应力的变化，非线性程度减弱了，因此数值分析的计算量也减小了，收敛性也可以保证。......
2025-09-29
-
系统预测的方法与占星术的思想互动详细阅读
把系统作为预测对象，了解系统发展变化的规律性，预测系统未来则称为系统预测。占星术是西方国家在预测时常用的技术。该预测技术充分地表现出古人宇宙观的智慧。预测带来的这种消极的、唯心的思想，我们要加以警惕。......
2025-09-29
相关推荐