数海拾贝：古埃及的割补近似方法

2023-11-23 理论教育版权反馈

【摘要】：古埃及人用割补近似法求平方根。古埃及人的基本思路是,先构造一个矩形,再把矩形割补成一个馨折形。图3.7.1古埃及人切割矩形使之接近正方形图3.7.2古埃及人把矩形化为馨折形在需要平方根时,古埃及人总是把问题改动一下,使得其正好能得出平方根,但如上所述,这并不意味着所有平方根都是整数。可以推测,古埃及人有一张足够大的平方数表,而将该表反过来查就可得到平方根。

现有资料表明,尼罗河在馈赠给古埃及人几何知识的同时,也送去了与之相关的其它数学知识。埃及人求圆面积的计算方法是化圆为方,结果较为精确。他们将直径减去其1/9 之后再平方,即圆面积s=(8d/9)2,其中d 表示直径。这相当于取π=3.1605(中国古人取圆周率为3),不过他们似乎并无圆周率概念。

古埃及人用割补近似法求平方根。例如,求的平方根就相当于求一个面积为的正方形的边长。古埃及人的基本思路是,先构造一个矩形,再把矩形割补成一个馨折形(正方形去掉一个角)。其具体做法为:构造一个宽为,长为 pagenumber_ebook=192,pagenumber_book=183 的矩形,然后在长边剪下一个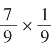的小矩形,放置在短边上。这样所得馨折形的面积即为,与边长为的正方形仅相差,所以可将作为的平方根的近似值。

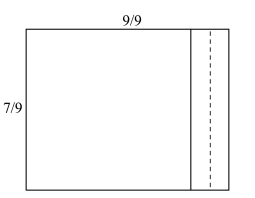
pagenumber_ebook=192,pagenumber_book=183

图3.7.1　古埃及人切割矩形使之接近正方形(www.chuimin.cn)

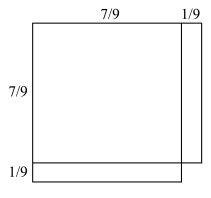
pagenumber_ebook=192,pagenumber_book=183

图3.7.2　古埃及人把矩形化为馨折形

在需要平方根时,古埃及人总是把问题改动一下,使得其正好能得出平方根,但如上所述,这并不意味着所有平方根都是整数。在纸草书中有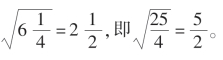 pagenumber_ebook=192,pagenumber_book=183 他们用“”表示根号。可以推测,古埃及人有一张足够大的平方数表,而将该表反过来查就可得到平方根。能够建造金字塔和巨大神殿的事实,足以说明埃及人已积累了较为丰富的实用数学知识。

数海拾贝：古埃及的割补近似方法

相关推荐