数学发展史：不等号的起源及发展

2025-09-30 理论教育版权反馈

【摘要】：不等关系的经常出现,自然引起了数学家的关注,他们试图采用简洁的符号来表示之。按照以出版时间为准的国际惯例,严格不等号应该算诞生于1631 年,然而此时哈里奥特已逝世10 年了,故可推测不等号肯定是在1621 年前创立的。至18 世纪初哈里奥特创立的严格不等号通用起来。图3.6.2哈里奥特除哈里奥特注意到不等号互相对称的特性外,还有不少数学家亦注意到这一点。我国古代没有不等号,皆是以文字来叙述不等关系。

不等关系的经常出现,自然引起了数学家的关注,他们试图采用简洁的符号来表示之。最早尝试者是荷兰数学家吉拉德,在其《代数新发现》中,他用AffB 表示A >B,用BξA表示B<A。尽管所给“大于”和“小于”符号不具备对称性,但这迈出的第一步甚是重要。值得一提的是,吉拉德给出了数学上著名的“代数基本定理”,即n 次代数方程具有n个根。

现在使用的严格不等号“ <”“ >”是英国数学家哈里奥特(T.Harriot,1560—1621)创立并最早建议使用的。他是英国代数学派的奠基人,其遗著《实用分析学》(Artis Analyticae Praxis)发表于1631 年,该书在韦达研究的基础上,主要讨论了代数方程相关理论。哈里奥特进一步发展了代数符号体系。他用元音代表未知数,辅音代表常数,但用小写字母比用大写字母要多。同时还创立了乘法符号和减法符号,然而最有价值的是“大于号”和“小于号”的创立。他写道:

大于记号:a>b 表示a 量大于b 量;

小于记号:a<b 表示a 量小于b 量。

显然,哈里奥特的这对符号比吉拉德的记号简洁优美,尤其是突出了互为相反的特征,很快就得到一些学者的认可和赞许。按照以出版时间为准的国际惯例,严格不等号应该算诞生于1631 年,然而此时哈里奥特已逝世10 年了,故可推测不等号肯定是在1621 年前创立的。至18 世纪初哈里奥特创立的严格不等号通用起来。

pagenumber_ebook=188,pagenumber_book=179

图3.6.2　哈里奥特

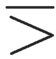除哈里奥特注意到不等号互相对称的特性外,还有不少数学家亦注意到这一点。如英国数学家奥特雷德(W.Oughtred,1570—1660)于1631 年在著作《数学之钥》(Clavis Mathematicae)中创用符号“ pagenumber_ebook=188,pagenumber_book=179 ”表示大于,符号“”表示小于。值得注意的是,在该书中哈里奥特还首次以符号“ ×”表示乘。同时代神学家、数学家沃利斯(John Wallis,1616—1703)则与奥特雷德相反,他用符号“”表示小于,符号“”表示大于。据说沃利斯曾在1655 年用符号“ pagenumber_ebook=188,pagenumber_book=179 ”表示等于或大于,后又于1670 年写为“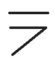”(等于或大于)并创用符号“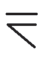”(等于或小于)。(https://www.chuimin.cn)

第一个把等号和不等号合起来组成新符号“≥”“≤”者,应是法国数学家布格尔(P. Bouguer,1698—1758)。其父是水文学家和数学家,致力培养儿子研究相同专业。布格尔还发明了测日计来测量太阳及其它发光体的光强。他在其书中创立了不严格不等号,但他未充分认识到其重要性,直到被哥德巴赫发现。哥德巴赫于1734 年1 月写信告知欧拉,欧拉立刻给予肯定,称赞这对符号既保持了等号和不等号双重关系,还如此简洁优美。故现在把符号“≥”“≤”的创立时间确定为1734 年。

我国古代没有不等号,皆是以文字来叙述不等关系。其中最著名的不等式应是祖冲之(429—500)所确定的圆周率取值范围

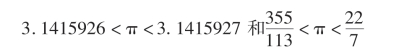
pagenumber_ebook=189,pagenumber_book=180

据《隋书·律历志》记载,祖冲之以直径为1 丈的圆,求得圆周率介于肭数3.1415926 和盈数3.1415927 之间。这两个近似值准确到小数点后第7 位,是当时世界上最先进的数学成就。祖冲之还确定了π 的两个渐近分数:约率22/7 和密率355/113。其中密率355/113 是三个成对奇数113355 从中间折成两段组成的,形式优美、规整、易记。

不等号首先由清末数学家李善兰(1811—1882)引进中国。 1852 ～1859 年,李善兰与英国传教士伟烈亚力(A. Wylie,1815—1887)等合译出版了《几何原本》后九卷及《代数学》《代微积拾级》等,这是西方近代科学著作传入中国的开端。其中李善兰引进了西方的大量数学符号,同时还创译了许多科学名词,如“数轴”“函数”“代数”等,可谓匠心独运,贴切恰当,沿用至今。

不等关系在我们日常生活中经常出现,如“大与小”“长与短”“高与矮”“优与劣”“胖与瘦”等。而在数轴上,显然右边的数永远大于左边的数。只要留意身边的事情,就会发现大量不等关系。

数学发展史：不等号的起源及发展

相关推荐