或许在整个数学中，还找不到另一个定理，其证明方法之多能够超过毕达哥拉斯定理，不同的时代，不同的国家和地区，不同职业的人物都在寻找定理的新的证明方法.据说，在中世纪，要求取得数学学位的学生必须提供毕达哥拉斯定理的原创证明，这激发了学生和老师们不断提供新的、有创意的证明方法.美国克里夫兰西部高中数学教师卢米斯（1825—1940）在他做教师的50年间，收集整理了毕达哥拉斯定理的371种证明，出版了一本......
2023-11-19
毕达哥拉斯定理的发现和证明，以及其背后的故事
【摘要】：据传毕达哥拉斯学派为庆祝该定理的发现曾宰杀百牛祭祀缪斯女神,但这与该学派所奉行的素食主义相悖。后人对毕达哥拉斯发现和证明勾股定理有各种猜测。图3.2.14毕达哥拉斯定理图3.2.15毕达哥拉斯定理的证明一般认为,毕达哥拉斯采用了剖分方法来证明定理。因而就有化简后则得到毕达哥拉斯定理。《几何原本》中的毕达哥拉斯定理图3.2.16毕达哥拉斯纪念碑3.2.17《几何原本》命题473.2.18希腊1955 年邮票毕达哥拉斯定理是《几何原本》第一卷命题47。
西方称勾股定理为毕达哥拉斯定理,其叙述也与中国有所区别:直角三角形斜边上的正方形面积等于两直角边上的正方形面积之和。 据传毕达哥拉斯学派为庆祝该定理的发现曾宰杀百牛祭祀缪斯女神,但这与该学派所奉行的素食主义相悖。 后人对毕达哥拉斯发现和证明勾股定理有各种猜测。
(1)定理的发现
某天毕达哥拉斯到朋友家做客,发现朋友家用砖所铺成地面的图案反映了三个正方形A、B、C 面积之间的数量关系,即A+B =C。 回家后他仍苦苦思考着该问题,突然灵光闪现,悟出了定理的证明。 据传他当时紧紧抱着妻子大声喊道:“我终于证明了!”
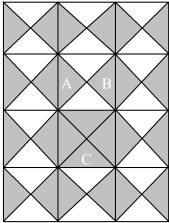
图3.2.14 毕达哥拉斯定理
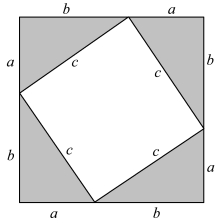
图3.2.15 毕达哥拉斯定理的证明
一般认为,毕达哥拉斯采用了剖分方法来证明定理。 如图3.2.15 所示,设a,b,c 分别表示直角三角形的两条直角边和斜边,考虑边长为a+b 的正方形,该正方形被分成4 个全等直角三角形和一个以斜边为边长的正方形。 因而就有
化简后则得到毕达哥拉斯定理。
在毕达哥拉斯的家乡萨摩斯岛上,修建了一座毕达哥拉斯纪念碑,其形状为直角三角形,有个巨人仰望天空,举起手臂试图连接起直角边,那个巨人就是毕达哥拉斯(图3.2.16)。
(2)《几何原本》中的毕达哥拉斯定理
(www.chuimin.cn)
图3.2.16 毕达哥拉斯纪念碑
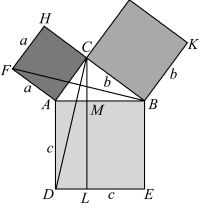
3.2.17 《几何原本》命题47
3.2.18 希腊1955 年邮票
毕达哥拉斯定理是《几何原本》第一卷命题47。 欧几里得的证明思路如图3.2.17 所示:作CL 垂直于DE,则该线分正方形BADE 为二部分,可证其面积分别与其斜上方两个小正方形面积相等。 具体方法是:先证△FAB≌△CAD,再由三角形面积是同底等高的平行四边形面积的一半,知△FAB 的面积是正方形FACH 的一半,△CAD 的面积是矩形ADLM 的一半,得证。
欧几里得的证明还告知我们,如何作出一个正方形使其面积等于所给两个正方形之和,即求x,使x2 =a2 +b2。
由于《几何原本》流传广泛,欧几里得给出的定理证明最为著名。 希腊人称之为“已婚妇女定理”,阿拉伯人称之为“新娘图”“新娘座椅”,在欧洲还被称为“孔雀尾巴”“圣人头巾”和“大风车”等。 两千年来世界上不同文字的《几何原本》对这一颇具特色的定理证明都附插图,异文同图,饶有趣味。
欧几里得还给出了毕达哥拉斯定理的逆定理:
命题48 若三角形一边上的正方形面积等于其它两边上的正方形面积之和,则其它两边的夹角是直角。
勾股定理是欧几里得几何中三角形边角关系的重要表现形式,虽属于直角三角形情形,但也不失一般性。 故欧几里得在《几何原本》第一卷,以勾股定理为核心展开,一方面奠定了其公理体系架构,另一方面围绕勾股定理的证明,揭示了面积的自然基础,并在第二卷将勾股定理推广到任意三角形,给出余弦定理。
从多元文化视角看,勾股定理是全人类共同的文化精华。 更有趣的是,华罗庚曾想象,勾股定理可作为地球人与外星人交流的语言。 作为人类智慧的结晶,勾股定理实可谓是几何学的明珠,千百年来始终散发着无穷无尽的光彩。
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
罗尔定理的证明和费马定理的基本性质详细阅读
从几何上可以看到：在对于两端高度相等的连续光滑曲线上，必存在一条水平的切线（如图3－1所示），这便是罗尔定理.为了罗尔定理证明的需要，下面先给出极值的定义和极值点的一条基本性质——费马定理.图3－1定义1设f（x）在点x0的某邻域内有定义，若x∈（x0，δ），恒有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x0）为f（x）的一个极大值（或极小值），函数的极大值与极小值统称为函数的极值......
2023-11-19
-
毕达哥拉斯定理的发现与世界各地的数学成果详细阅读
与人类文明的其他重要成就一样，毕达哥拉斯定理的发现不是某个人在某个时刻的灵光闪现，不同的国家和地区的人们在不同的时期，各自独立地得到这一发现.我国现存最早的有关天文学和数学的著作是《周髀算经》，成书年代大概在公元前2世纪，而书中的内容当然还要早.据记载，商高在回答周公关于数学计算的问题时答曰：“……故折矩，以为勾广三，股修四，径隅五……”......
2023-11-19
-
天台山的命名由来及其背后的故事详细阅读
此前台州天台的读音尚不至于如此混淆。台州以天台山得名，天台山的“台”读如怀胎十月的“胎”，天台的“台”也是“胎”字的声符。台州天台的读音应当遵循“名从主人”的原则，这样才能保持地名特有的音义内涵，才能体现文化的多样性和地方性。......
2023-07-18
-
毕达哥拉斯学派及其贡献——毕达哥拉斯定理与带详细阅读
这是毕达哥拉斯纪念碑,碑体呈直角三角形形状．毕达哥拉斯是古希腊哲学家、数学家,创建了宗教、政治、学术合一的著名的毕达哥拉斯学派,该学派信奉“万物皆数”,发现了毕达哥拉斯定理,定义了奇数、偶数、完全数、亲和数等概念,研究了图形数的规律．知能概述用一个正整数b去除另一个正整数a,若商为q,余数为r,则有a＝bq＋r．余数有以下基本性质:b|(a－r);一个正整数a被另一个正整数n(n＞1)除时,余数只可能是0,1,2,…......
2023-08-13
-
毕达哥拉斯定理：一本书揭示科学发现史详细阅读
毕达哥拉斯学派将算术和几何紧密联系起来。毕达哥拉斯学派最大的贡献在数学方面，最著名的就是“毕达哥拉斯定理”，该定理在中国称为勾股定理，即直角三角形斜边的平方等于两直角边的平方和。而毕达哥拉斯定理的发现，实际上导致了无理数的发现，尽管毕达哥拉斯学派不愿意接受这样的数，并因此形成了数学史上所谓的第一次数学危机，但是毕达哥拉斯学派的探索仍然是功不可没的。不过毕达哥拉斯定理的证明，还应归功于毕达哥拉斯。......
2023-08-16
-
毕达哥拉斯定理：数学课中的珍宝详细阅读
费马的研究是建立在自毕达哥拉斯以来一直到他的时代大量知识的基础上的.费马在数论领域的第一个发现涉及所谓的“亲和数”.亲和数是这样的一对数，其中的一个数是另一个数的因数之和，如早期的毕达哥拉斯学派得到的220和284（其中220的因数有1，2，4，5，10，11，20，22，44，55，110，它们的和是284；另一方面，284的因数是1，2，4，71，142，它们的和是220），直到1636年才由......
2023-11-19
-
铷和铯的发现及其重要性详细阅读
铷和铯是由本生和基尔霍夫发现的。本生和基尔霍夫发明的光谱分析法，被称为“化学家的神奇眼睛”，一直到今天，它还在闪闪发亮。1862年，本生加热碳酸铷和焦炭的混合物，制得了金属铷。......
2023-11-24
相关推荐