古希腊时期对正多边形的认识

2023-11-23 理论教育版权反馈

【摘要】：古希腊数学家毕达哥拉斯发现,16 与18 可同时等于一个矩形(正方形)的面积和周长,而其它自然数不具备这种特性。帕波斯的唯一传世之作《数学汇编》是一部荟萃总结前人成果的杰作,许多古希腊宝贵的数学资料都因该书记载而得以保存下来。这是因为在所有正多边形中,只有正六边形、正方形和正三角形这三种正多边形才能够镶嵌平面,使得镶嵌好的平面不留空隙。而在上述三种图形中,当其面积相等时,正六边形具有最小的周长。

正方形是特殊的平行四边形,亦是特殊的矩形和菱形,故它具有很多漂亮的几何性质。古希腊数学家毕达哥拉斯发现,16 与18 可同时等于一个矩形(正方形)的面积和周长,而其它自然数不具备这种特性。如边长为4 的正方形,其周长和面积都是16;边长为3,6 的矩形,其面积和周长均是18。证明如下:

假设矩形的相邻两边长分别为x,y,则有方程

pagenumber_ebook=145,pagenumber_book=136

易见,x 的取值只能是3,4,6,对应的y 值则为6,4,3。故xy只可能是16 和18。

可能受时代限制,毕达哥拉斯学派没有给出正方形的表示符号,最早应用正方形象形符号“□”者,是公元50 年左右的古希腊数学家海伦。他不仅修订和注释了欧几里得的《几何原本》,还著有《量度》,主要讨论了各种几何图形的面积和体积计算,包括以其名字命名的三角形面积公式

其中,Δ 为三角形面积,a,b,c 为边长,s=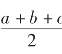 pagenumber_ebook=145,pagenumber_book=136 。

后来的数学家帕波斯(Pappus,约公元300—350)也许是沿用了海伦的表示方法,其亦使用了“□”符号表示正方形。帕波斯的唯一传世之作《数学汇编》是一部荟萃总结前人成果的杰作,许多古希腊宝贵的数学资料都因该书记载而得以保存下来。当然其中也有帕波斯自己的科学贡献,最为突出的是圆周问题:在周长相等的平面图形中,圆的面积最大。帕波斯还考察了蜂巢结构的若干极值性质。(www.chuimin.cn)

读者见过正五边形或正七边形的地板砖吗? 应该没有吧。这是因为在所有正多边形中,只有正六边形、正方形和正三角形这三种正多边形才能够镶嵌平面,使得镶嵌好的平面不留空隙。而在上述三种图形中,当其面积相等时,正六边形具有最小的周长。这就意味着在蜂巢建造过程中,获得同样的空间,蜜蜂把其窝建成正六边形所使用的蜂蜡最少,所付出的劳动也最少。

正六边形的形状还可在雪花、分子、晶体、海洋生物等其它物体中找到。

pagenumber_ebook=146,pagenumber_book=137

图2.8.1　蜂巢

pagenumber_ebook=146,pagenumber_book=137

图2.8.2　用六边形砖铺设地板

古希腊时期对正多边形的认识

相关推荐