虽然人类对角的认识由来已久,但直至埃里冈才第一次给出角的表示符号“ <”。埃里冈选用符号“ =”表示平行大概亦是基于如此理念,但当时欧洲已使用符号“ =”作为等号,为避免混乱,英国数学家奥特雷德改用符号“∥”来表示平行,显然是将等号逆时针旋转45 度并拉长而得到。埃里冈采用符号“◇”表示平行四边形,现在看来有些勉强。......
2023-11-23
数学符号的创用及其影响
【摘要】：例如,法国数学家克莱罗曾建议用大写希腊字母作为函数符号,如∏x,Φx,Δx 等。对于函数定义,欧拉先后给出了三个。后又把函数定义为“任意画出的一条曲线”。欧拉被后人称为“数学家之英雄”,是因为其顽强拼搏的毅力和惊人的创造力震撼了世人的心灵。图2.3.4数学看起来高深莫测可见,数学符号中不仅有英文字母,还有希腊字母,这是沿用了历史上数学家的做法,即约定俗成。
此后,很多数学家开始关注函数研究和函数表示。 例如,法国数学家克莱罗(Alexis-Claude Clairaut,1713—1765)曾建议用大写希腊字母作为函数符号,如∏x,Φx,Δx 等。 然而数学界公认,对函数发展做出卓越贡献者应是约翰·伯努利的得意门生欧拉(Leonhard Euler,1707—1783)。
欧拉13 岁就进入了巴塞尔大学学习,其数学老师是约翰·伯努利。 他喜欢勤学好问的欧拉,虽然研究工作很忙,但把每个周六下午都留给欧拉,师生共同探究数学问题,总是和蔼可亲地诠释欧拉的所有疑问。
1734 年,欧拉用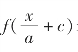
表示
的函数,此乃数学史上第一次用f(x)来表示x 的函数。 其创造灵感源于拉丁语“函数”术语,选取第一个字母,并巧妙地加上了一个括号,在其中填写自变量。
对于函数定义,欧拉先后给出了三个。 1748 年所给函数定义为:一个变量的函数是由该变量和一些数或常量以任何方式所构成的解析式。 后又把函数定义为“任意画出的一条曲线”。 1775 年所给函数定义为:若某变量以某种方式依赖于另一些变量,即后者变化时前者也随之而变化,则称前者为后者的函数。
欧拉被后人称为“数学家之英雄”,是因为其顽强拼搏的毅力和惊人的创造力震撼了世人的心灵。 即使双目失明之后,欧拉也毫不气馁,仍不停地进行科学研究,或口述给秘书,或在石板上推导数学公式。 “如果命运是块顽石,我就化作大铁锤,将它砸得粉碎!”这就是欧拉的人生态度。 在全盲的17 年中,欧拉先后发表了400 余篇高水平论文。 他关于函数的第三个定义体现了“对应性”,反映了从“自变量”到“因变量”的依赖过程,是函数科学定义的雏形。 而该定义就是欧拉在全盲身体状况下创造的,这的确令人叹服!
1797 年,法国数学家拉格朗日为追求函数定义的严密性,建议用幂级数来定义函数,并推广了欧拉的函数符号,用英文字母f,F 和希腊字母Φ,Ψ 来表示函数,加上括号和自变量即为f(x),F(x),Φ(x),Ψ(x)。
图2.3.4 数学看起来高深莫测(www.chuimin.cn)
可见,数学符号中不仅有英文字母,还有希腊字母,这是沿用了历史上数学家的做法,即约定俗成。 美国数学家克莱因(M.Kline,1908—1992)说,数学家在论文中喜欢用希腊字母,这是因较之英文字母,希腊字母显得更为神秘一些,故更会让外行觉得数学高深莫测。 若果真如此,说明数学家有时也会故弄玄虚!
现行初中课本的函数定义诞生于1837 年,这应归功于两位德国数学家黎曼(G.F.B.Riemann,1826—1866)和狄利克雷(G.L. Dirichlet,1805—1859)。 他们所给函数定义逻辑清晰、层次完美,很快被数学界所接受。 同时他们又把欧拉的函数表示改进为y=f(x),即y 是x 的函数。
图2.3.5 黎曼
图2.3.6 狄利克雷
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
数学符号演进的观点：数学海拾贝详细阅读
从数学意义上来讲,未知量的表示符号经历了较长的演进过程。值得一提的是,李冶的创举也影响了欧洲的数学符号表示。图2.7.2方程算筹表达式法国数学家韦达的数学符号体系导致了代数学的重大变革。直到1911 年辛亥革命后,政府主张采用国际上通行的先进数学符号,从此x 及其它数学符号方才逐步进入了中国数学。正是数学家们创立各种符号的努力带来了今日数学的简洁和美丽,促进了数学的迅速发展。......
2023-11-23
-
符号串及其运算符号集合的定义与性质详细阅读
典型的符号有字母、数字、各种标点符号和各种运算符。定义B-7（符号串）由符号集∑中0个或多个符号相连而成的有穷序列称为∑上的符号串。包括空串在内的∑上符号串的全体记为∑。如果x是符号串，把x自身连接n(n≥0)次得到的符号串x，称为x的n次方幂，记作xn。定义B-11设V是符号集∑上的一个符号串集合，则V的正闭包定义为V的闭包定义为例如：V={a，b}，则V+={a，b，aa，ab，ba，bb，aaa，aab，…......
2023-06-28
-
圆周率符号π：数学和数学家的故事详细阅读
新生事物的出现往往会引来一些嘲讽,琼斯的圆周率符号也不例外。由于数学大师们的影响,圆周率符号π 得到了广泛认可和应用。反观国内,在我国古代圆周率没有明确的符号表示。直至20 世纪初期,我国数学教科书由直排改为横排之时,才与世界数学接轨,用符号π 表示圆周率。如在1932 年的《初级混合算学》中,就载有“圆周与直径之比,通常表示以π”。......
2023-11-23
-
基本符号及其变量的相依性详细阅读
定义1.3 称随机变量X1，…定义1.4 对于随机变量序列｛Xk；k≥1｝，如果对每个n和所有的x1，…，xn，都存在某一独立于n的正常数M，使得（1.5）式和（1.6）式同时成立，则称｛Xk；k≥1｝是广义负相依序列。定义1.5 两个非负随机变量X1和X2是拟渐近独立的，如果如果X1和X2同分布，那么就说它们是渐近独立。如果随机变量序列｛Xk，k≥1｝中的任意两个随机变量都是QAI的，则称｛Xk；k≥1｝是两两AQI序列。......
2023-07-06
-
电流的符号、单位及其表示方法详细阅读
电流的大小是在单位时间内通过导体任一截面的电荷量。电流的符号用I表示。测量时，把电流表串联在电路中，如图7-1所示。在电路中对电流通过有阻碍作用且造成能量消耗的元件称为电阻。电阻常用符号R或r表示，单位是欧姆，简称欧（Ω），也常用千欧（kΩ）或者兆欧（MΩ）作为单位。导体的电阻由导体的材料、横截面积和长度决定。电阻可以用万用表欧姆挡测量。测量时，要选择电表指针偏转量程一半的欧姆挡。......
2023-06-26
-
巴比伦与波斯：古代月份及其符号详细阅读
三月：西马奴相当于我们现在的5月中旬—6月中旬四月：杜乌朱相当于我们现在的6月中旬—7月中旬。这些月份的名称来源于阿卡德的塞姆语，但所用的符号却是尼普尔的苏美尔的楔形符号。这种以阿卡德语发音读苏美尔月份符号的方法一直被延续，直到楔形文字死亡。三月＝西马奴＝双子之月。六月＝乌鲁鲁＝处女之月。九月＝基斯里穆＝射手之月。十月＝台贝图＝魔羯之月。十一月＝沙巴图＝宝瓶之月。......
2023-11-01
-
《数学教学论》：数学语言及其教学详细阅读
数学发展史表明，数学的发展与数学语言的创造是分不开的。我国数学教育学者郑毓信指出，应当将熟练掌握数学语言作为数学教育的一个基本目标，包括帮助学生学会数学地表达，数学地理解等，也就是说，我们不应将“数学地说”与“数学地写”等仅仅看成帮助学生掌握相应的数学知识与技能的一种手段，而应将其本身看成数学教育的重要目标之一因此，探究数学语言的特点及其教学是很有意义的。......
2023-08-13
相关推荐