数学家鲁道夫：圆周率的精确计算和平方根符号的演化

2023-11-23 理论教育版权反馈

【摘要】：直到16 世纪,法国数学家拉米斯仍用“L27adL12 等于L75”表示。英文平方根单词“square root”与拉丁文平方根单词“radix”渊源较深,历史上一度曾用radix 表示平方根。用符号“R”作为平方根号首次出现在阿拉伯文版《几何原本》之中。如1525 年,鲁道夫在其《求根式》中,用8 表示。值得一提的是,鲁道夫几乎耗尽了一生时间求圆周率精确值,计算至圆内接正262 边形,并于1609 年得到了圆周率的35 位精确值,以至圆周率在德国被称为Ludolph(鲁道夫)数。

从公元前2500 年左右起,古埃及人就用一种僧侣文来作日常书写。这套文字最初只是象形字的缩写,尽管其有限的数学符号尚不成体系,但已有了加法、减法和平方根符号,其用符号“ pagenumber_ebook=110,pagenumber_book=101 ”来表示平方根。故平方根符号是最早出现的数学符号之一,这主要是因数学在现实生活中的广泛应用。例如计算圆和正方形面积时,需要πr2,x2 这样的数学式子,而其逆运算就是求平方根,这自然就加快了数学史上平方根符号的出场速度。

公元2 世纪,罗马数学家尼普萨斯用拉丁文单词Latus(正方形之边)表示平方根,其后“L”就逐渐成为欧洲的平方根符号。直到16 世纪,法国数学家拉米斯(R. P. Ramus,1515—1572)仍用“L27adL12 等于L75”表示。 1624 年,英国数学家布里格斯(H. Briggs,1561—1631)仍沿用罗马人的符号,并且分别用L,L3,LL 表示平方根、立方根和四次方根。

平方根与无理数有着一定联系。在古印度语中,无理数的“无理”为“carani”,7 世纪印度数学家婆罗摩笈多就用其第一个字母C 来表示平方根,如ru3C45 表示3 + 45。婆罗摩笈多提出了负数概念,并用小点或小圈记在数字上面以表示负数。他的负数概念及其加减法法则仅晚于中国而早于其他国家,而其负数乘除法法则领先于世界。后来的印度相关数学文献中,平方根则用“kapaha”一词的“ka”来表示。

15 世纪的阿拉伯数学家阿尔·卡拉萨迪(Al-Qalasadi)曾用阿拉伯文根号术语“jidr”的首写字母“j”表示根号,其用法是将该符号放在所要求平方根的数字之上,有时会在符号和文字之间用一条水平线加以分隔。

英文平方根单词“square root”与拉丁文平方根单词“radix”渊源较深,历史上一度曾用radix 表示平方根。如radix de 5 et radix de 13 表示5 + 13。现在看来,将“radix”简化为“R”比较自然,故而就有了后来用“R”表示平方根。(www.chuimin.cn)

用符号“R”作为平方根号首次出现在阿拉伯文版《几何原本》之中。 12 世纪的意大利数学家斐波那契曾随父到印度、埃及、阿拉伯和古希腊等地旅行,师从阿拉伯人学习算学知识,回意大利后写成《算经》,其中把“R”用作平方根号和未知数。《算经》在欧洲的影响较大,也就导致符号“R”通用了好几百年。如卡尔达诺(G.Cardano,1501—1576)在其《大法》中,也用“R”表示平方根,且用“cu”表示立方根,式子R·7 表示7。

欧洲其它一些地区曾用其它一些符号作为根号。在1480 年前后,德国人曾用“·”表示平方根,两点“··”表示4次方根,三个点“···”表示立方根,如·3 表示3。至16 世纪初,小点带上了一条小尾巴,这也许是书写快时带上的,在此基础上又逐渐演变成了“ pagenumber_ebook=112,pagenumber_book=103 ”。如1525 年,鲁道夫在其《求根式》中,用8 表示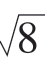。值得一提的是,鲁道夫几乎耗尽了一生时间求圆周率精确值,计算至圆内接正262 边形,并于1609 年得到了圆周率的35 位精确值(参见本书1.16),以至圆周率在德国被称为Ludolph(鲁道夫)数。

1629 年埃尔伯特(G. Albert,1595—1632)在其著作中,将开方次数放在“ pagenumber_ebook=112,pagenumber_book=103 ”左上方,用以表示开几次方根,如三次方根写为“3”,但对于开四次方根,他却使用了符号“”。

数学家鲁道夫：圆周率的精确计算和平方根符号的演化

相关推荐