双曲几何也否定了这一公设：双曲几何中，平行线有无穷多条。其中，曲率为零的部分满足欧几里得几何，曲率为正的部分满足球面几何，而曲率为负的部分满足的是双曲几何。双曲几何对应的是负曲率的空间区域。......
2023-11-22
黎曼几何：常曲率空间及其重要性
【摘要】：在黎曼几何中,最重要的研究对象就是所谓常曲率空间。黎曼指出后两种情形分别对应于罗巴切夫斯基几何和欧几里得几何,而第一种情形则是其本人的创造。表1.10.2三种几何学的比较黎曼可以说是最先理解非欧几何全部意义的数学家,其创立的黎曼几何不仅承认了已有的非欧几何,而且显示了创造其他非欧几何的可能性。
是金子总会发光的,1854 年罗巴切夫斯基几何思想得到进一步发展:时年28 岁的德国数学家黎曼(1826—1866)建立了一种更为广泛的几何学,即黎曼几何。
在黎曼几何中,最重要的研究对象就是所谓常曲率空间。 对于三维空间有三种情形:曲率为正常数,曲率为负常数,曲率恒等于零。 黎曼指出后两种情形分别对应于罗巴切夫斯基几何和欧几里得几何,而第一种情形则是其本人的创造。 在这种新几何中,过已知直线外一点,不能作任何平行于已知直线的直线。 普通球面上的几何就是黎曼几何,其上每个大圆可看成一条“直线”,易见球面上的“直线”都是相交的,而且三角形内角和皆大于180°。
表1.10.2 三种几何学的比较
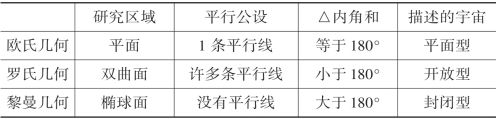
黎曼可以说是最先理解非欧几何全部意义的数学家,其创立的黎曼几何不仅承认了已有的非欧几何,而且显示了创造其他非欧几何的可能性。 但黎曼理论仍难以被同时代的学者所理解。 为了照顾多数听众,黎曼在其演讲中删除了许多数学技巧性细节,然而除年迈的高斯外,几乎没有人能听懂他所讲的内容。(www.chuimin.cn)
直到19 世纪70 年代,非欧几何才真正被学界普遍接受。这得益于意大利数学家贝尔特拉米(E. Beltrami,1835—1900)、德国数学家克莱因(F. C. Klein,1849—1925)和法国数学家庞加莱(H. Poincaré,1854—1912)等先后在欧几里得空间中给出了非欧几何的直观模型,从而揭示了非欧几何的现实意义。
现在可谓多种几何学共存,已有多种非欧几何创立并发展。 非欧几何是人类认识史上一个富有创造性的伟大成果,其创立不仅带来了数学科学的巨大进步,而且对现代物理学、天文学及人类时空观念的变革都产生了深远影响。
“质疑”和“推广”是数学家的根本素养。 从“质疑”平行公设到创立非欧几何,其中凝结着无数数学家的努力和心血,我们应学习其执着求真精神。 数学学习是一种生动活泼、积极主动和富有个性的活动。 数学学习作为一种乐趣、一种享受、一种对数学奇境的探索,可使学习者成为具有创新意识的探索者,体验到数学科学的神奇与价值。
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
曲率空间变化-2页纸图解数学详细阅读
所以，我们用1/r来代表这条线在该点处的曲率，其中r是密切圆的半径。曲率可以为正，可以为负，正负取决于曲线的方向。曲率在空间内可随着点的变化而变化：张量场可以很好地来表示它。参考阅读//No. 60 流形，第124页No. 65 张量场，第134页No. 74 度量空间，第152页No. 76 维度，第156页No. 79 双曲几何，第162页3.一分钟记忆直观上，我们将曲率理解为一条线在某点处的弯曲程度，在此基础上，我们可以进一步测量任意一个空间的弯曲程度。......
2023-11-22
-
《导数的几何意义及其应用》详细阅读
【主要内容】设函数f（x）在点x0处可导，则f′（x0）是曲线y=f（x）在点（x0，y0）（y0=f（x0））处切线的斜率.曲线y=f（x）在点（x0，y0）处的切线方程为y-y0=f′（x0）（x-x0）.当f′（x0）≠0时，曲线y=f（x）在点（x0，y0）处的法线方程为注 （ⅰ）如果f′（x0）=∞，则曲线y=f（x）在点（x0，y0）处的切线方程为x=x0；如果f′（x0）=0，则曲线......
2023-10-27
-
几何晶体学的建立及其应用详细阅读
布拉维于1848年指出，弗兰根海姆的15种空间点阵形式中有两种实质上是相同的，确定了空间点阵的14种形式。在19世纪的最后十年中，几何晶体学理论已全部完成了。几何晶体学虽然在19世纪末已成为系统的学说，但直到1912年以前它还仅仅是一种假说，尚未被科学实验所证实。当时没有一个科学家想到要把X射线和几何晶体学这两件几乎同时出现的重大科学成就联系起来。......
2023-11-24
-
空间几何体特征揭秘-机电应用数学详细阅读
在现实世界中，存在着各种各样的物体，它们都占据着一定的空间.如果只考虑这些物体的大小和形状，而不考虑其他因素，那么由这些物体抽象出来的空间图形就叫做空间几何体.观察与思考仔细观察下面的图片，你能说出它们都是什么建筑吗？棱锥的结构特征观察与思考观察下面图片，说说图片中的几何体具有什么样的共同特征呢？......
2023-11-22
-
欧氏空间常平均曲率嵌入的闭超曲面，证明是球面详细阅读
，en＋1，限制于N，en＋1是N的单位外法向量，ω1，ω2，…，xn＋1的二次函数，即这里aB和b都是实常数，x1，x2，…，xn＋1是Rn＋1内直角坐标系的坐标．由方程的边界条件，公式限制在M上，有这恰说明闭超曲面M是Rn＋1内n维球面．下面讲述另一个著名的定理．设M是n＋1维欧氏空间Rn＋1内一个n维嵌入超曲面．由第1章第6讲公式，可以知道这里R是M的数量曲率，平均曲率由定义．由第1章第7讲公式......
2023-11-23
-
空间理论的重要性与应用详细阅读
空间理论上，列斐伏尔反对传统社会理论单纯视空间为社会关系演变的平台，反之指出它是社会关系至为重要的组成部分，空间既是在历史发展中生产出来，又随历史的演变而重新结构和转化。《空间的生产》中列斐伏尔分析了物质、精神、社会三种空间。福柯指出，空间成为理论关注的对象并不是新鲜事情，因为我们时代的焦虑与空间有着根本关系。此外像休闲、工作、游戏、交通、公共设施等，无不涉及空间的概念。......
2023-07-31
-
高校图书馆引进创客空间可行性研究-常弘详细阅读
高校图书馆引进“创客空间”可行性研究常 弘[摘 要]介绍了创客空间的概念、创客空间的产生及发展、图书馆成立创客空间的意义以及实施方案、阐述了高校图书馆服务引入创客空间的意义、实施方式以及图书馆建设创客空间的注意事项。第一创客空间在我国高校图书馆还是个比较新生的事物，师生对此还不是很了解，为此我们要扩大宣传，使师生了解图书馆创客空间的服务项目。......
2024-08-31
相关推荐