马克思曾为自己能把高等数学的某些公式应用于经济学研究而高兴。在《资本论》中,马克思不仅把数学作为计算工具,而且作为科学的逻辑论证方法。马克思的数学兴趣与其哲学兴趣也是紧密联系的。马克思把研究数学作为丰富辩证法的重要源泉之一。马克思作为思想家,其知识之渊博,其思想之精深,其著作之丰厚,可与历史上任何伟大的思想家相媲美。......
2023-11-23
杰克·伦敦所给的数学问题-数海拾贝揭秘
【摘要】：美国现实主义作家杰克·伦敦从1900 年起连续发表和出版了许多小说,讲述美国下层人民的生活故事,揭露资本主义社会之罪恶。对数学颇有研究的杰克·伦敦在其小说里叙述了一道趣味数学题:某人乘坐5 条狗拉的雪橇从斯卡洛维伊赶回营地。故到达营地的时间迟了2 昼夜。小说未给出问题的答案,也许是故意留给读者思考。该问题条件较多,数量关系较为复杂,不少读者最初可能抓不住解题的关键。故只要求出全速行进速度,问题就解决了。
美国现实主义作家杰克·伦敦从1900 年起连续发表和出版了许多小说,讲述美国下层人民的生活故事,揭露资本主义社会之罪恶。 著名作品有《马丁·伊登》《野性的呼唤》《白牙》《热爱生命》等小说。 在其家中到处贴满了形形色色的小纸条,其上写满了各种各样搜集的材料。 他每个衣袋中都装有纸卡片,以便出外访问途中加以浏览,并随身带着笔记本,以便随时记下所见所闻,还对所读一切材料均作了卡片索引,从而建立了储存写作素材的“参考阅览室”。
对数学颇有研究的杰克·伦敦在其小说里叙述了一道趣味数学题:某人乘坐5 条狗拉的雪橇从斯卡洛维伊赶回营地。 第一个昼夜雪橇全速行驶。 而第一个昼夜后,有2 条狗扯断缰绳跑掉了,只好由3 条狗来拉雪橇,前进速度减缓为原来的3/5。 故到达营地的时间迟了2 昼夜。 书中提示:若跑掉的2 条狗能再拉雪橇走50 英里,则能比预定时间只迟到一天。
读者自然会想:从斯卡洛维伊到营地有多远? 小说未给出问题的答案,也许是故意留给读者思考。 该问题条件较多,数量关系较为复杂,不少读者最初可能抓不住解题的关键。
分析:由“若跑掉的2 条狗能再拉雪橇走50 英里,则能比预定时间只迟到一天”知,再全速行驶50 英里,就能比预定时间迟到一天,进而推出再全速行驶
50 ×2 =100(英里)(www.chuimin.cn)
就能按时到达营地。 这说明第一天后离营地还有100 英里,而这100 英里行程是由3 条狗拉的,速度为原来的3/5,到了预定时间只走了60 英里,还剩下40 英里未跑完,这剩下的40 英里就是多跑2 天的原因(迟到了2 昼夜)。 故只要求出全速行进速度,问题就解决了。
解:设5 条狗全速前进速度为v 英里/日,则3 条狗行进速度为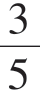
v 英里/日,有分式方程
易得
因而从斯卡洛维伊到营地的距离为
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
研读《数海拾贝：数学和数学家的故事》，探寻数详细阅读
表1.6.1马克思求解不定方程数值表因x=10 时,y=0,与题意不符,故前9 组均为方程的解。约从19 世纪60 年代起,马克思开始学习微积分,研读了牛顿的《自然哲学的数学原理》、欧拉的《无限分析引论》《微分学基础》、穆瓦尼奥的《微分学讲义》、拉克罗阿的《微积分学》、布沙拉的《微积分学与变分学》、赫明的《初等微积分学》、拉格朗日的《解析函数论》、达朗贝尔的《流体论》等在数学史上影响较大的著述。......
2023-11-23
-
数海拾贝：毕达哥拉斯学派的数学音乐观详细阅读
据传,某日毕达哥拉斯经过一家铁匠铺,被富有节奏的打铁声所吸引,于是便走进铺子,细心观察,发现音响是否和谐与发声体体积的比例有关。毕达哥拉斯学派认为,万物皆数,世界就是数之和谐。毕达哥拉斯学派赋予每个数字特定的含义。毕达哥拉斯音阶为:在毕达哥拉斯看来,音乐最能对生活方式起到净化作用。......
2023-11-23
-
数海拾贝：古代中国音乐中的数学理论详细阅读
中国古代音乐创作中也应用了数学。所谓“生于度量”,即音律的确定需要数学。在中国最早利用数学制订出十二平均律的是明朝朱载堉。图3.20.1朱载堉纪念馆朱载堉的十二平均律精确规定了八度的比例,并把八度分成12 个半音,使相邻两个半音的频率比是常数。即2b=bq12q=1221.059463据十二平均律,各音级频率构成指数函数。十二平均律是目前世界上通用的把一个八度分成十二个半音音程的律制,这种律制包括了乐音的标准音高、乐音的有关法则和规律。......
2023-11-23
-
莱布尼茨创立全等符号-来自《数海拾贝》的数学详细阅读
创立三角形全等符号者是德国数学家莱布尼茨,其被誉为“百科全书式天才人物”,研究兴趣非常广泛,涉及哲学、历史、语言、数学、生物、地质、物理、机械、神学、法学、外交等,并且在每个领域中皆做出了卓越贡献。莱布尼茨可谓是数学史上最伟大的符号学者之一,堪称一代数学符号大师。为了使全等符号更加合理且避免与上述数学符号相互混淆,莱布尼茨创造了全等符号“≌”。......
2023-11-23
-
数海拾贝：古埃及的割补近似方法详细阅读
古埃及人用割补近似法求平方根。古埃及人的基本思路是,先构造一个矩形,再把矩形割补成一个馨折形。图3.7.1古埃及人切割矩形使之接近正方形图3.7.2古埃及人把矩形化为馨折形在需要平方根时,古埃及人总是把问题改动一下,使得其正好能得出平方根,但如上所述,这并不意味着所有平方根都是整数。可以推测,古埃及人有一张足够大的平方数表,而将该表反过来查就可得到平方根。......
2023-11-23
-
《数海拾贝》：托尔斯泰的割草之谜详细阅读
为此,我们也可以假设每人每天割草面积为1,则有关系式托尔斯泰没有设定未知数求解,而是应用构图法求解,构思巧妙,解法简捷,是“割草问题”最为简捷的解法,几乎不用动笔即可解之。......
2023-11-23
-
数海拾贝：攻克难题，不放弃发稿详细阅读
在哈尔滨电机厂工作期间,陆家羲阅读了孙泽瀛的《数学方法趣引》,所介绍的“柯克曼女生问题”和“斯坦纳系列问题”强烈地吸引了他,此后这两个组合设计问题再也没有同他的生活分离。该文于1966 年2 月被退稿。从1961 年到1983 年,陆家羲共撰写了20 余篇研究论文,除6 篇于他去世前后发表在美国《组合论杂志》上,其余均向国内刊物投稿,结果不是退稿就是石沉大海。......
2023-11-23
相关推荐