和一维情形类似，通过对F的二维傅里叶逆变换可恢复原函数f(x,y)。二维傅里叶变换运算举例设，求它的傅里叶变换。......
2025-09-30
正三角形剖分与傅里叶
【摘要】：法国数学家傅里叶对正三角形也颇有研究。图1.8.4三角形剖分成25 个三角形图1.8.5三角形剖分成49 个三角形傅里叶首先考虑了一些特殊情形,如先把一个正三角形的三条边5 等分,然后适当连接这些等分点,便得到一系列面积相等的小正三角形。显然有1 +3 +5 +7 +9 =25 =52这让傅里叶很兴奋,接着他又把一个正三角形的三条边7 等分,得到72 =49 个小正三角形。
法国数学家傅里叶(1768—1830)对正三角形也颇有研究。 同塔塔利亚一样,傅里叶也有着悲惨的童年,他9 岁时父母双亡,幸好有位主教收养了他。 4 年后他被送到教会主办的当地一所军事学校学习。 傅里叶的才能很快就显现出来,特别是其文学写作能力受到全校师生的赞誉,他的文章具有很强的雄辩性和鼓动性,乃至巴黎一些教堂的传教士纷纷来请他撰写布道文。 一次偶然机会,傅里叶接触了数学,神奇的数学世界使他流连忘返。 他常把厨房和角落里的蜡烛头收集起来,以备晚上读书学习。
1789 年法国大革命爆发后,新兴的资产阶级建立了一些新型的教育、科学机构。 1794 年巴黎高等师范学校创立,第二年巴黎综合工科学校也创立了,这标志着法国数学新时代的开始。 在这两所国际著名的学校里,傅里叶表现出卓越的数学才华。
1798 年傅里叶追随拿破仑(B.Napoléon,1769—1821) 远征埃及。1801 年返回法国后,担任伊泽尔行政区行政长官,同时继续其数学理论研究。 1807 年傅里叶将论文《热解析理论》提交法国科学院,而评审委员会批评该文缺乏严密性,为此他愤愤不平。 1811 年傅里叶把修改后的论文再次提交科学院,虽然赢得了大奖,但评审委员会仍认为该论文缺乏严密性,故未刊登在法国科学院院刊上,这极大地伤害了傅里叶的自尊心。 10 年之后,傅里叶当选为法国科学院终身秘书,他把自己后来的那篇论文一字未改地发表在科学院院刊上。
图1.8.3 傅里叶
数学家往往都有一些怪癖。 傅里叶一生主要研究热传导理论,埃及的行军经历竟使其相信:身体保持高温对健康有益。 他经常在身上裹好几层布,像木乃伊一样,并且使室内保持着比撒哈拉沙漠还要高的温度。 这显然不利于身体健康,最终导致其1830 年死于心脏病。
傅里叶追随拿破仑远征埃及期间,曾来到数学家毕达哥拉斯的故乡,看到那些悠久的古代文明遗迹,敬佩之情油然而生。 眺望着远方的金字塔,他突发奇想:对于一个正三角形,能否将其剖分成m2 个全等的小正三角形?
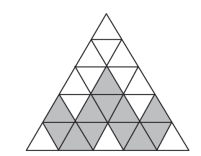
图1.8.4 三角形剖分成25 个三角形
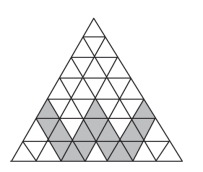
图1.8.5 三角形剖分成49 个三角形
傅里叶首先考虑了一些特殊情形,如先把一个正三角形的三条边5 等分,然后适当连接这些等分点,便得到一系列面积相等的小正三角形。 显然有
1 +3 +5 +7 +9 =25 =52
这让傅里叶很兴奋,接着他又把一个正三角形的三条边7 等分,得到72 =49 个小正三角形。 自然可把问题推广到一般情形,他把三角形三条边均分成m 等份,然后分别连接等分点,这样就得到(https://www.chuimin.cn)
1 +3 +5 +7 +9 +…+(2m-1) =m2
对于这个一般结论,傅里叶感到很欣慰。
将问题稍微推广一点:若已知图1.8.4 中阴影部分面积是294 cm2,求图1.8.5 中阴影部分面积。 初看两个图形中小三角形大小不一,难以计算其面积。 然而注意到,两个大三角形边长相等,应用相互之间的比例关系则可确定。
因图1.8.4 阴影部分小三角形有12 个,而图1.8.5 阴影部分小三角形有16 个,且前者阴影部分面积是294 cm2,故后者阴影部分面积为
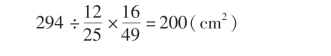
傅里叶回到法国后,在杂志上看到一个问题:能否把一个三角形剖分成12 个全等的小三角形? 他还是考虑了特殊情形,即对于一个正三角形容易剖分成12 个全等三角形(图1.8.6),但对于一般三角形没有解决。 不过他发现了下面事实:
若直角三角形的两条直角边之比为1∶ 2,则可剖分成5个全等的小直角三角形,且其与原直角三角形相似。
傅里叶的作法很简洁,如图1.8.7 所示。 若假设原直角三角形的两条直角边长分别是1 和2,则其斜边长为5,显然小直角三角形斜边长为1,而两条直角边长分别为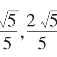
。
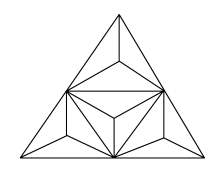
图1.8.6 正三角形剖分成12 个三角形
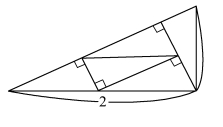
图1.8.7 直角三角形剖分成5 个三角形
相关文章
- 详细阅读
-
剖切面分类及应用技巧详细阅读
画由单一斜剖切平面剖切获得的剖视图时应注意以下几点。3）单一剖切柱面的应用国家标准规定：采用单一剖切柱面剖切获得的剖视图应按展开画法绘制，如图6-22所示的B—B展开图为采用单一剖切柱面获得的局部剖视图。如图6-23所示的主视图就是采用三个互相平行的剖切平面获得的全剖视图。......
2025-09-29
-
傅里叶定律及其基本概念详细阅读
基本概念①温度场温度场是指某一时刻空间各点温度的总称。傅里叶定律傅里叶在实验研究导热过程的基础上，把热流矢量和温度梯度联系起来，得到q=λgradt 上式就是1822年由傅里叶提出的导热基本定律的数学表达式，亦称为傅里叶定律。傅里叶定律确定了热流密度矢量和温度梯度的关系。......
2025-09-30
-
复变函数中的傅里叶积分公式详细阅读
定理1(傅氏积分定理) 若函数f(x)在(-∞,+∞)内有定义,且满足(1)在任一有限区间上满足狄利克雷条件,即在任意区间内满足: 连续或只有有限个第一类间断点; 只有有限个极值点;(2)在无限区间(-∞,+∞)内绝对可积(即积分收敛),则在f(x)的连续点上有成立,而左端的f(t)在它的间断点t处,应以来代替.这个定理称为傅里叶积分定理,简称为傅氏积分定理,其中所列的条件是充分的,它的证明需要用......
2025-09-30
-
傅里叶光学原理-互相关函数详细阅读
对于不满足绝对可积条件，即能量无限的信号，如果满足功率有限条件，若平均功率都收敛，这类信号称为功率有限信号，其互相关函数可用平均功率来定义，即或简写为上述互相关函数的定义可以直接推广到二维。......
2025-09-30
- 详细阅读
-
旅游景区质量等级划分与评定方法详细阅读
前 言本标准从实施之日起，代替GB／T 17775—1999《旅游区（点）质量等级的划分与评定》。本标准由国家旅游局提出。同时，根据GB／T17775—1999《旅游区（点）质量等级的划分与评定》国家标准自1999年至今近3年时间的实施情况，在原标准基础上对一些内容进行了修订，使其更加符合旅游区（点）的发展实际。游乐园达到GB／T 16767—1997规定的安全和服务标准。......
2025-09-30
-
热熔胶的成分与特性及测试要求详细阅读
熔融后的EVA热熔胶，呈浅棕色或白色。EVA热熔胶由基本树脂、增黏剂、黏度调节剂和抗氧化剂等成分组成。由于胶体在高温熔融状态下会发生氧化反应，加入抗氧化剂可以保证胶体在高温条件下黏结性能不发生变化，防止EVA热熔胶的过早老化。试验过程中热熔胶无发烟、相分离、凝胶现象；无沉淀，无颜色变化，软化点和熔融黏度符合《YC/T 187—2004烟用热熔胶》表1技术指标要求的为合格，否则该项指标为不合格。......
2025-09-29
相关推荐