为了防备坏狐狸来偷吃鸡宝宝,鸡妈妈找来许多木板和木棍搭了一间平顶小木房。坏狐狸一看骗不成,就露出了狰狞的面目。喜鹊衔来三根树枝,摆了一个三角形。晚上,坏狐狸又来了。坏狐狸鼓足了劲再摇,还是丝毫不动。他们还把上头削尖了,防止坏狐狸跳进来。坏狐狸围着木栅栏转了两圈,发现还是搞毁栅栏门最容易。陷阱底全是三角形的禾尖钉,狡猾的狐狸丧了命。鸡妈妈高兴地说：“三角形用处可真大呀!”......
2023-11-06
塔塔利亚、锈规和正三角形的数学故事
【摘要】：此乃著名的锈规作图问题。塔塔利亚家里很穷,因交不起学费一生仅仅上学两个星期。这当然难不住生性聪慧的塔塔利亚,他很快就作出了边长为a 的正三角形。图1.8.1塔塔利亚图1.8.2锈规作正三角形(小)分别以BE、AF 为底,用锈规作边长为b 的正三角形△EGB 和△AHF,而其边AH、BG 相交于一点C,由于∠CAB=∠CBA=60°,故△ABC 为所求。1983 年美国几何学家佩多发现:若给定两点A 和B,其距离大于1 个且小于2 个锈规跨度,则可作出正三角形。
利用尺规作图画正三角形,其作法相当简单:先用直尺画出一条任意长度的线段(等边三角形边长),再分别以线段两个端点为圆心、以线段长度为半径画弧,只要在两交点中任选一点,和原线段两个端点连接,则构成一个正三角形。
你是否想过用生锈的圆规来作正三角形? 此乃著名的锈规作图问题。 所谓“锈规”,就是圆规生锈了,导致其两脚张角不能改变。 应用锈规作图肯定有困难,但也是有可能的。
意大利数学家塔塔利亚(Tartaglia,1499—1557),其名意为“口吃者”,他原姓Fontana。 在塔塔利亚儿时,法国军队占领了意大利,一士兵枪杀了其父亲,还刺伤了塔塔利亚的颔部和舌头,使他丧失了准确说话的能力。 塔塔利亚家里很穷,因交不起学费一生仅仅上学两个星期。 在母亲指导下,他完全凭借自学在数学上取得了很大成就。 塔塔利亚的《论数字与度量》是16 世纪最优秀的数学著作之一,他最重要的数学成就是发现了一元三次代数方程的一般解法。
塔塔利亚曾在一所学校教学糊口。 他买不起好圆规,有次上课时发现其圆规已经锈住了。 他要作一个边长为a 的正三角形,但锈圆规的跨距却为b(a <b)。 这当然难不住生性聪慧的塔塔利亚,他很快就作出了边长为a 的正三角形。
其作法为(如图1.8.2 所示):将线段AB =a 左右延长,再分别以A、B 为圆心,用锈规画弧,截得BE=AF=b。
图1.8.1 塔塔利亚(www.chuimin.cn)
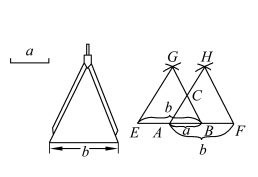
图1.8.2 锈规作正三角形(小)
分别以BE、AF 为底,用锈规作边长为b 的正三角形△EGB 和△AHF,而其边AH、BG 相交于一点C,由于∠CAB=∠CBA=60°,故△ABC 为所求。
这个做法甚是漂亮! 自然想到,当a >b 时,能否用锈规作出正三角形?
1983 年美国几何学家佩多(D.Pedoe)发现:若给定两点A 和B,其距离大于1 个且小于2 个锈规跨度,则可作出正三角形。 作法此处从略。
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
达·芬奇的数学情结：数学家的故事详细阅读
达·芬奇深刻认识到数学方法的重要性,并掌握了一些数学原理。在《最后的晚餐》中,达·芬奇应用了大量数学知识。达·芬奇的其他代表作《蒙娜丽莎》《岩间圣母》等也为世人所赞扬。......
2023-11-23
-
数学和数学家的故事：三角形和平行四边形详细阅读
命题41 若一个平行四边形和一个三角形既同底又在两平行线之间,则平行四边形面积是三角形的2 倍。图3.12.7《几何原本》卷一命题43若AC 为ABCD 的对角线,则其所谓平行四边形补形为BGKE 和KFDH。利用三角形全等可以证明之。图3.12.8《几何原本》卷一命题44若已知线段为AB,直线角为D,三角形为C,求作以AB为一边、某底角等于∠D、面积等于三角形C 的平行四边形。连接BD,则问题就转化为作两个平行四边形,其面积分别等于两个三角形的面积。......
2023-11-23
-
虎狈为奸的故事-数学童话故事详细阅读
老虎瞪圆眼睛仔细看了看这只狈,说：“有一句成语叫‘狼狈为奸’,说的就是你吧?”狈笑起来比夜猫子叫还难听,“不愧是兽中之王,连人间的成语都知道。不错,‘狼狈为奸’说的就是我和狼在一起可以干出许多好事。”老虎一愣,问,“和你合作不就成了‘虎狈为奸’了吗?”老虎非常高兴,扭头就去找小花猪哼哼。哼哼觉得老虎说的有点道理。......
2023-11-06
-
中国概率论的发展：数学与数学家的故事详细阅读
据现有资料分析,中国概率论可划分为5 个发展阶段。许宝騄是20 世纪最富有创造性的统计学家之一,是中国最早从事概率论与数理统计研究并达到世界先进水平的优秀数学家。其研究成果已经成为概率论与数理统计理论的重要组成部分,至今“许方法”仍被认为是解决检验问题的最实用方法。此为中国概率论学科发展的重要里程碑。......
2023-11-23
-
幼儿思维数学游戏：有趣三角形详细阅读
图一图二活动目标1.感知三角形的多种变式，体验图形的翻转与变化。活动准备不同形状三角形共18个；城堡拼图底板2幅（见图四）；磁性板3块（见图五）。活动难点运用翻转、旋转变化等方法变换三角形，解决游戏中的问题。活动过程一、游戏“找朋友”1.认识不同变式的三角形提问：看看这些三角形都相同吗？虽然它们长得不一样，但它们都有三条边、三个角，都是三角形。......
2023-08-15
-
函数概念引入中国：数学家和数学的故事详细阅读
直至1859 年,数学术语“function”才被引进中国,如何准确翻译成汉语没有先例。现今函数概念及其表示符号可谓充斥着数学王国,也成为我们生活中的重要组成部分。回顾17 世纪上半叶到现在300 余年函数概念的演进历程,充分表明了严密化的企图始终刺激着数学科学的发展。从笛卡儿、莱布尼茨、欧拉,再到李善兰,他们对函数的发展均做出了重要贡献,故函数概念及其表示符号实在是经过了千锤百炼,是一代代数学家集体智慧的结晶。......
2023-11-23
-
《测圆海镜》：李冶的数学故事详细阅读
《测圆海镜》共分12 卷,其以洞渊九容为基础,讨论了在各种条件下用天元术求圆径问题。《测圆海镜》无疑是当时世界上第一流的数学宏作,但因其内容较为精深,一般人难以读懂,致使“天元术”传播较为缓慢。......
2023-11-23
相关推荐