据现有资料分析,中国概率论可划分为5 个发展阶段。许宝騄是20 世纪最富有创造性的统计学家之一,是中国最早从事概率论与数理统计研究并达到世界先进水平的优秀数学家。其研究成果已经成为概率论与数理统计理论的重要组成部分,至今“许方法”仍被认为是解决检验问题的最实用方法。此为中国概率论学科发展的重要里程碑。......
2023-11-23
达·芬奇的数学情结：数学家的故事
【摘要】：达·芬奇深刻认识到数学方法的重要性,并掌握了一些数学原理。在《最后的晚餐》中,达·芬奇应用了大量数学知识。达·芬奇的其他代表作《蒙娜丽莎》《岩间圣母》等也为世人所赞扬。
“真理只有一个,它不在宗教中,而是在科学中。”艺术大师达·芬奇(L.da Vinci,1452—1519)笃信科学真理,不仅在美术领域而且在自然科学领域取得了惊人的成就。 诸如在物理学领域,重新发现了液体压力,提出连通器原理;在解剖学和生理学上,掌握了人体解剖知识,研究了生理学和医学,被誉为“近代生理解剖学始祖”;他还提出了飞行机械、直升机、降落伞、机关枪、手榴弹、坦克车、潜水艇、双层船壳战舰、起重机等设想。 米兰护城河是由他设计和督造的。 据说自行车传动原理也由其发明。 他坚信科学知识源于实践,必须通过实践活动去探索大自然的奥秘。 他所提出的实验科学方法,后经英国哲学家培根(Francis Bacon,1561—1626)提升,成为近代自然科学的基本方法,为伽利略、开普勒、牛顿等科学大师的研究提供了利器。
达·芬奇深刻认识到数学方法的重要性,并掌握了一些数学原理。 “不理解数学者将迷失在混乱之中。”“所有透视图像实例皆可用点、线、角、面和体这五个数学术语来说明之。”“不懂数学者不要读我的书。”“凡是和数学没有联系的地方均不可靠。”“没有什么能不通过实践探求而称为科学,除非它通过数学的解释和证明。”在其手稿中,有些画满了几何图形,有些则写着数字、算式和数学符号。
在《最后的晚餐》中,达·芬奇应用了大量数学知识。 该作品描绘的是,耶稣和12 门徒坐在餐桌旁,共庆逾越节,这是他们一起用的最后一顿晚餐。 达·芬奇以几何图形为基础设计画面,利用透视学原理,使观众感觉房间随画面作了自然延伸。 为了构图需要,作者使12 个门徒坐得比正常就餐的距离更近,并分成四组,在耶稣周围形成波浪状层次,愈靠近耶稣的门徒情绪愈激动。 耶稣被画成等边三角形,坐在正中间,摊开双手镇定自若,和周围情绪紧张的门徒形成鲜明对比。 耶稣双目注视画外,仿佛看穿了世间一切。 其背后的门外是一派祥和景色,明亮的天空在他头上仿佛是一道美丽光环。
图1.3.1 作品《最后的晚餐》
据说即使在米兰,想看这幅伟大作品也不容易,因为《最后的晚餐》是画在修道院的食堂墙壁上,而食堂里能容纳的人很少,一次只能进去25 人,每人只能看上15 分钟,因此参观者需要预约。
达·芬奇的其他代表作《蒙娜丽莎》《岩间圣母》等也为世人所赞扬。 他最大的贡献就是运用明暗法使平的画面呈现出空间感和立体感,这离不开将数学原理与美学原理相互结合,他有目的地使画像符合黄金分割,可以说其作品中处处表现出对数学的强烈兴趣。
《蒙娜丽莎》:蒙娜丽莎坐姿优雅,背景山水幽深茫茫,淋漓尽致地发挥了画家那奇特的烟雾状“无界渐变着色法”笔法。 蒙娜丽莎的脸是典型的黄金分割,造就了一种神秘莫测的千古奇韵,那如梦似的妩媚微笑被誉为“永恒的神秘微笑”。
图1.3.2 作品《蒙娜丽莎》(www.chuimin.cn)
图1.3.3 作品《岩间圣母》
《岩间圣母》:圣母居图中央,其右手扶婴孩圣约翰,左手下坐婴孩耶稣,天使在耶稣身后构成稳定三角形,并以手势彼此响应。 背景则是一片幽深岩窟,花草点缀,洞窟通透露光。 人物背景的微妙刻画、烟雾状笔法的运用、科学的写实以及透视缩形等技法的采用,表明作者在处理逼真写实和艺术加工的辩证关系方面达到了新的水平。
《维特鲁威人》:一裸体健硕中年男子,两臂微斜上举,两腿叉开,以其头、足和手指为端点外接一个圆形。 同时清楚可见叠着另一幅图像:男子两臂平伸站立,以他的头、足和手指为端点外接一个正方形。 所画男子形象被公认符合最完美的人体黄金比例。 男子被置正方形中,其边长为96 指长(24 掌长),而该正方形大部分被围在圆里,男子肚脐就是圆心。 此外,“神秘数字67”即素描圆周长67 厘米、素描人物头手夹角67°,以及素描人物耻骨横线与叉开的左右腿之间的夹角67°,也是个有趣的数学之谜。
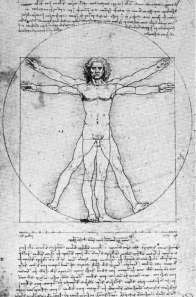
1.3.4 作品《维特鲁威人》
图1.3.5 《算术集成》插图
达·芬奇的数学情结与同时代数学家帕乔利密切相关,他常向后者请教数学问题,作为回报为其绘制了《算术集成》的插图,形象直观地图解了有关的数学原理和法则。 也正是画这些插图使达·芬奇熟练掌握了几何透视方法,作起画来得心应手。 恩格斯称他“不仅是大画家,还是大数学家、力学家和工程师”。
有关数海拾贝：数学和数学家的故事的文章
- 详细阅读
-
圆周率符号π：数学和数学家的故事详细阅读
新生事物的出现往往会引来一些嘲讽,琼斯的圆周率符号也不例外。由于数学大师们的影响,圆周率符号π 得到了广泛认可和应用。反观国内,在我国古代圆周率没有明确的符号表示。直至20 世纪初期,我国数学教科书由直排改为横排之时,才与世界数学接轨,用符号π 表示圆周率。如在1932 年的《初级混合算学》中,就载有“圆周与直径之比,通常表示以π”。......
2023-11-23
-
研读《数海拾贝：数学和数学家的故事》，探寻数详细阅读
表1.6.1马克思求解不定方程数值表因x=10 时,y=0,与题意不符,故前9 组均为方程的解。约从19 世纪60 年代起,马克思开始学习微积分,研读了牛顿的《自然哲学的数学原理》、欧拉的《无限分析引论》《微分学基础》、穆瓦尼奥的《微分学讲义》、拉克罗阿的《微积分学》、布沙拉的《微积分学与变分学》、赫明的《初等微积分学》、拉格朗日的《解析函数论》、达朗贝尔的《流体论》等在数学史上影响较大的著述。......
2023-11-23
-
西方分式方程理论：数学和数学家的故事详细阅读
英国著名盲人数学家、剑桥大学第四任卢卡斯数学教授桑德森可能是西方第一个研究分式方程的数学家。作为其解题过程的一部分,桑德森接着给出上述解法的逆过程。可见他已意识到解分式方程的过程应该是可逆的,但其是否知道在分式方程变换过程中可能出现增根和失根问题尚待进一步考证。若设乙所需天数为x,则甲为x+4,因而可列分式方程易得x=10。......
2023-11-23
-
因式分解的起源和方法-数学家的故事详细阅读
因式分解的最初目的是为了快捷求解代数方程,对此许多数学家做了尝试,最终凝练成我们今天熟知的一些规律。韦达和哈里奥特韦达在其《论方程的整理和修改》中,首先给出代数方程的多项式因式分解方法,并证得所有三次和三次以上的一元多项式在实数范围内皆可因式分解。笛卡儿与因式分解1637 年笛卡儿在其《几何学》中,首次应用待定系数法将4 次方程分解为两个2 次方程求解,并最早给出因式分解定理。......
2023-11-23
-
《九章算术》开方术：数学家的故事详细阅读
在中国《九章算术》第四章少广篇12 ～16 题中,应用了开平方计算,并在16 题后给出了较为完整的开平方法。复置结算步之如初,以复议一乘之,所得副,以加定法,以除。现以第12 题为例说明中国古代的开平方法:今有面积为55225 平方步的正方形,求其边长。两位两位地数:5,52,25,最高位数字是5,而5 包含的最大完全平方数是4,其算术平方根为2。以议得的2 乘10000 得20000,将其放在实之下、借算之上,称之为“法”。......
2023-11-23
-
刘徽与《九章算术》：数学家的故事详细阅读
图1.1.3邮票上的刘徽图1.1.4隶首造数《九章算术》的历史贡献分数、负数、无理数、比例、方程、面积诸多数学知识皆可在《九章算术》中找到源头。后世数学家多从《九章算术》开始研究数学。在唐宋两朝,《九章算术》皆由国家明令规定为教科书。《九章算术》早在隋唐时期已传入朝鲜、日本。现在《九章算术》已被译成英、日、俄、德、法等多种文字。......
2023-11-23
-
函数概念引入中国：数学家和数学的故事详细阅读
直至1859 年,数学术语“function”才被引进中国,如何准确翻译成汉语没有先例。现今函数概念及其表示符号可谓充斥着数学王国,也成为我们生活中的重要组成部分。回顾17 世纪上半叶到现在300 余年函数概念的演进历程,充分表明了严密化的企图始终刺激着数学科学的发展。从笛卡儿、莱布尼茨、欧拉,再到李善兰,他们对函数的发展均做出了重要贡献,故函数概念及其表示符号实在是经过了千锤百炼,是一代代数学家集体智慧的结晶。......
2023-11-23
相关推荐