声音的传播介质有空气、液体和固体,它们分别称为空气声、液体声和固体声等。人类生活在一个声音的环境中,通过声音进行交谈、表达思想感情,以及进行各种活动。这些为人们生活和工作所不需要的声音称为噪声。从物理现象判断,一切无规律的或随机的声信号叫噪声;噪声的判断还与人们的主观感觉和心理因素有关,即一切不希望存在的干扰声都叫噪声。......
2025-09-30
模糊数学已在环境科学领域中得到了应用,如在环境评价、环境污染物分类、环境区域划分等方面,用模糊数学方法进行数据处理,结果与实际更接近、更可信。
模糊数学是用数学方法来解决一些模糊问题。所谓模糊问题是指界限不清或隶属关系不明确的问题,而环境评价中“污染程度”的界限就是模糊的,人为地用特定的分级标准去评价环境污染程度是不确切的。如评价河流污染时,用内梅罗公式计算总污染指数I,把I≤1作为一级轻污染河水的指标,若实际情况是I=1.02,则算作二级污染河水,这完全是人为的规定;若改用隶属度表示,则可认为当I=1.0时,河水隶属于一级轻污染河水的程度达到100%,而当I=1.02时,河水隶属于一级轻污染河水的程度只达到98%,相应地认为该河水隶属于二级污染河水的程度为2%。采用隶属度的概念来表达客观事物是模糊数学的基点,由此可以去研究众多模糊问题。本节简单介绍环境监测数据的模糊综合评价和聚类分析。
(一)模糊综合评价的基本知识
1.模糊子集和隶属函数
在集合论中,把具有某种特定属性的对象的全体称为集合,而集合里所含有的个体,叫作集合的元素。又把所讨论的全体对象称为论域,以u或v表示;论域中的元素以相应的ui、vi(i=1,2,⋯,n)表示。给定论域u中的某一部分元素的全体称为u上的一个集合,常以A、B表示。在思维中每个概念都有一定的外延与内涵。外延是指适合于某个概念的一切对象,而内涵则是指外延包括的一切对象所具有的本质属性。显然,内涵就是集合的定义,而外延则是组成该集合的所有元素,模糊概念没有明确的内涵和外延。例如:清洁和污染等,它们对应的是模糊集合,记为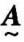 、
、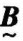 等。
等。
一个普通集合A,元素x与A的关系只能有x∈A或x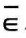 A,这种集合可以用特征函数来描述,即定义:
A,这种集合可以用特征函数来描述,即定义:
在描述一个模糊集合时,可以在普通集合基础上把特征函数取{0,1}两值扩大到[0,1]区间上连续取值,这就能借助于经典数学定量地描述模糊集合。取值在[0,1]上的模糊集合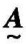 的特征函数为隶属函数,记为
的特征函数为隶属函数,记为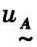 (x)。
(x)。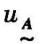 (x)的值表示了元素x隶属于模糊集合
(x)的值表示了元素x隶属于模糊集合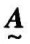 的程度:
的程度: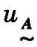 (x)=0,表示
(x)=0,表示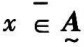 ;
; (x)的值接近于1,表示x隶属于
(x)的值接近于1,表示x隶属于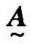 的程度很高。
的程度很高。
2.模糊集合的运算
对于一个普通集合的基本运算有:并、交、补、包含关系等,但模糊集合的基本运算有所不同,由于模糊集合用隶属函数来表征,因此可用隶属函数运算来定义模糊集合的运算。
(1)若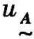 (x)=
(x)= (x),则称
(x),则称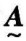 =
=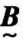
(2)若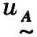 (x)=0,则称
(x)=0,则称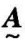 为空模糊集合,记作∅;若
为空模糊集合,记作∅;若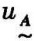 (x)=1,则称
(x)=1,则称 为全集。
为全集。
(3)若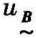 (x)≤
(x)≤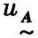 (x),则称
(x),则称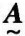 包含
包含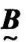 ,记为
,记为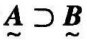
模糊集合的基本运算有并、交、补等。
设有两个模糊集合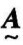 、
、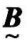 ,它们的并集为
,它们的并集为 ,交集为
,交集为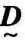 ,其隶属函数分别为:
,其隶属函数分别为:
其中,∨、∧分别表示取大值和取小值运算,即将两端较大的值和较小的值作为运算结果。
模糊集合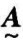 的补集
的补集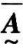 的隶属函数为:
的隶属函数为:
3.模糊矩阵运算
模糊矩阵运算与普通矩阵运算不同,模糊矩阵仍用大写字母下加浪纹号表示,模糊矩阵的一般形式为:
其中0≤aij≤1,i=1,2,⋯,m;j=1,2,⋯,n。
对于两个模糊矩阵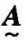 =[aij]和
=[aij]和 =[bij],若有
=[bij],若有
cij=max(aij,bij)=aij∨bij
则称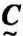 =[cij]为
=[cij]为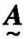 和
和 的并,记为
的并,记为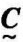 =
=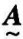 ∪
∪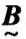 。
。
同样,若有
cij=min(aij,bij=aij∧bij
则称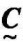 =[cij]为
=[cij]为 和
和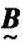 的交,记为
的交,记为 =
=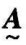 ∩
∩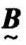 。
。
若有
则称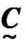 =[cij]为
=[cij]为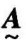 和
和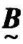 的乘积,记为
的乘积,记为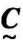 =
=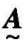 ·
·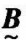 。
。
 的补矩阵
的补矩阵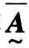 为:
为:
例如:若有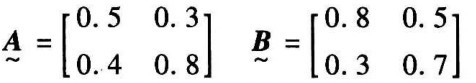
则
对于论域u上的模糊集合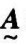 和
和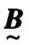 ,则称
,则称
分别为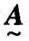 与
与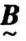 的内积和外积。在此基础上,称由下式
的内积和外积。在此基础上,称由下式
所确定的数为 和
和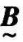 的贴近度,记为(
的贴近度,记为(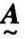 ,
,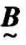 ),其值是[0,1]上的一个数。
),其值是[0,1]上的一个数。
(二)模糊综合评价
已知某因子集u=(u1,u2,⋯,un),其中,元素ui(i=1,2,⋯,n)为影响评价对象的各个因子,通常各因子的重要程度不一样,因此,对每个因子ui赋予一个相应的权重ai(i=1,2,⋯,n)构成权重集:
且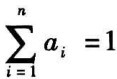 ,a ≥0(i=1,2,⋯,n)。
,a ≥0(i=1,2,⋯,n)。
由于ai可称为因子ui“重要”的隶属度,因此,权重集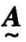 为因子集u上的一个模糊子集。
为因子集u上的一个模糊子集。
又设普通评价集:
V=(V1,V2,⋯,Vm)
元素Vj(j=1,2,⋯,m)为各种可能的评价结果,可以是模糊的,也可以是非模糊的,但它们对V的关系是明确的。
从一个因子ui出发进行评价,以确定评价对象对评价集元素Vj的隶属度rij (j=1,2,⋯,m),称为单因子模糊评价。对第i个因子ui评价的结果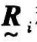 称为单因子模糊评价集:
称为单因子模糊评价集:
它是V上的一个模糊子集,于是可得到相应于每个因子的单因子模糊评价集:
将各单因子模糊评价集的隶属度为行组成单因子模糊评价矩阵:
显然,单因子模糊评价仅反映一个因子对评价对象的影响,而未反映所有因子的综合影响,也就不能得出综合的评价结果。因此,必须综合考虑所有因子的影响,这便是模糊综合评价。模糊综合评价集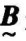 是V上的模糊子集,可表示为:
是V上的模糊子集,可表示为:
其中,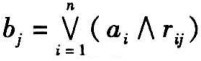 (j=1,2,⋯,m)称为评价指标,它是综合考虑所有因子的影响时,评判对象对评价集中第j个元素的隶属度。
(j=1,2,⋯,m)称为评价指标,它是综合考虑所有因子的影响时,评判对象对评价集中第j个元素的隶属度。
显然, 的第i行表示第i个因子影响评价对象取各个评价元素的程度;第列表示所有因子影响评价对象取第j个评价元素的程度。因此,每列元素再乘以相应因子的权重ai(i=1,2,⋯,n),更为合理地反映所有因素的综合影响。
的第i行表示第i个因子影响评价对象取各个评价元素的程度;第列表示所有因子影响评价对象取第j个评价元素的程度。因此,每列元素再乘以相应因子的权重ai(i=1,2,⋯,n),更为合理地反映所有因素的综合影响。
[例]应用模糊综合评价法,对某河流水质作现状评价。
解:(1)建立因子集。根据《地表水环境质量标准》(GB 3838—2002)的有关规定,确定水质影响因素共五项,即因子集为:
u=(DO,BOD5,IMn,挥发酚,氰化物)
(2)建立评价集。《地表水环境质量标准》把河流按功能高低分为五类,如下表。因此,评价集V=(Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ)。
(3)建立隶属函数。水质污染程度是一个模糊概念,水质分类标准也是模糊的,用隶属度来描述分类界线较为合理。如根据上表中DO的五类标准,作出DO对5个类别的隶属函数,即
DO—Ⅰ类
DO—Ⅱ类
DO—Ⅲ类
DO—Ⅳ类
DO—Ⅴ类
同样,根据BOD5的五类标准,作出BOD5对于5个类别的隶属函数,即
BOD5—Ⅰ类
BOD5—Ⅱ类
BOD5—Ⅲ类
BOD5—Ⅳ类(https://www.chuimin.cn)
BOD5—Ⅴ类
类似地作出IMn、挥发酚和氰化物的隶属函数(略)。
(4)单因子模糊评价。将实际监测数值,如DO=2.69mg/L、BOD5=2.5mg/L代入相应的隶属函数,计算其隶属度为:
DO:uⅠ(2.69)=0,uⅡ(2.69)=0,uⅢ(2.69)=0,uⅣ(2.69)=0.69,uv(2.69)=0.31
BOD5:uⅠ(2.5)=1,uⅡ(2.5)=0,uⅢ(2.5)=0,uⅣ(2.5)=0,uv(2.5)=0
类似地计算出IMn、挥发酚和氰化物的隶属度。
由此得到单因子模糊评价矩阵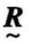 为:
为:
其中,第一行表示因子集u中第一个因子DO对5个类别的隶属度,即水质就DO而言,隶属于Ⅳ类的程度为0.69,隶属于Ⅴ类的程度为0.31,其余均为0;第一列表示u中5个因子分别对于Ⅰ类的隶属度。
(5)建立权重集。由于DO、BOD5等污染物对水质影响程度不同,因此,对它们应赋予不同的权重ai。确定权重有许多方法,以污染物的超标情况确定权重较为合理,其计算式为:
注意:对于DO,其权重取上式的倒数。
式中:
ai、ρi、ρs,i分别为第i种污染物的权重、质量浓度实测值和多级质量浓度标准值的平均值,ρs,ij为第i种污染物第j级质量浓度标准值,m为级别数。
为了进行模糊复合运算,各单因子权重必须归一化,即
应用上述方法确定本例的权重集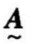 为:
为:
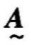 =(0.36,0.10,0.27,0.03,0.24)
=(0.36,0.10,0.27,0.03,0.24)
(6)模糊综合评价。
=(0.10,0.24,0.24,0.36,0.31)
对该河流的模糊综合评价只是V上的模糊子集,矩阵中各元素是对应于集合V上的各项的隶属度,即对Ⅰ类的隶属度为0.10,对Ⅱ类为0.24,对Ⅲ类为0.24,对Ⅳ类为0.36和对Ⅴ类为0.31,由于对Ⅳ类和Ⅴ类隶属度较大,故该河流水质认为处于Ⅳ类和Ⅴ类之间。
(三)模糊聚类分析
模糊聚类分析属于多元分析,用数学方法定量地确定被分类对象之间亲疏关系,从而客观地分型划类。模糊聚类分析可以分为两大部分:标定,即在被分类的全体对象之间建立一定的亲疏关系;分类,即以模糊等价关系进行分类。
描述样品的亲疏程度通常有两种途径:一种是把每个样品看成m维空间中的一个点,在点与点之间定义某种距离;另一种是用某种相似系数来描述样品间的亲疏关系。
1.距离和相似系数
设有n个样品,x1,x2,⋯,xn,每个样品都具有m个特性指标,用xij表示第i个样品的第j个特性指标,于是可得n个样品的观测数据矩阵:
其中n为样品数,m为变量(特性指标)数,记xi=(xi1,xi2,⋯,xim)。
为了刻画样品之间的接近程度,引入较为广义的距离概念。用dij表示第i个样品xi与第j个样品xj之间的距离,一般要求dij满足条件:①dj≥0且dii=0;②dij=dji;③dii≤dik+dkj对一切i、j)。
常用的距离有:
(1)汉明距离。
(2)欧氏距离。
(3)切比雪夫距离。
常用的相似系数有:
(1)夹角余弦。
(2)相关系数。
式中: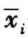 ——第i个样品各指标经标准化处理后的平均值。
——第i个样品各指标经标准化处理后的平均值。
(3)最大最小法。
(4)绝对值减数法。
使c取值满足0≤rij≤1。
在作环境质量分级时,究竟选择上述多种计算式中哪一种为好,不能一概而论,应根据实际情况选取。但是,选取的方法将直接影响分类结果。因而通常的做法是同时选取n种方法计算,最后看分类与实际吻合的情况,择优选取。
2.模糊等价关系
所谓模糊等价关系是指在给定论域u=(u1,u2,⋯,un)上一个模糊关系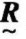 ,其相应的模糊矩阵记为
,其相应的模糊矩阵记为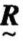 =[rij]n×n,如果矩阵满足:自反性,rii=1;对称性,rij=rji;传递性,
=[rij]n×n,如果矩阵满足:自反性,rii=1;对称性,rij=rji;传递性,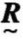 ○
○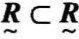 。则称模糊矩阵
。则称模糊矩阵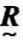 是一个模糊等价矩阵,以
是一个模糊等价矩阵,以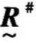 表示,其相应的关系称为模糊等价关系。
表示,其相应的关系称为模糊等价关系。
通常应用相似系数或距离方法建立起来的模糊矩阵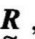 ,只能满足自反性和对称性,而不能满足传递性。该方法是作模糊矩阵
,只能满足自反性和对称性,而不能满足传递性。该方法是作模糊矩阵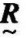 的合成运算:
的合成运算: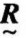 →
→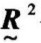 →
→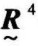 →⋯→
→⋯→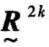 ,当
,当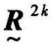 =
=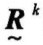 时,则
时,则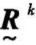 便是模糊等价矩阵
便是模糊等价矩阵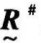 。
。
(四)模糊等价矩阵的截矩阵
模糊等价矩阵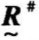 =[rij]的λ截矩阵
=[rij]的λ截矩阵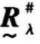 =[
=[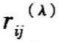 ]是一个布尔矩阵,其中:
]是一个布尔矩阵,其中:
显然,λ的值不同,其相应的截矩阵亦不同,由此而产生不同的分类数目。
[例]对某地遭受污染的河流进行水质监测。分别取5个断面的水样进行分析,各项监测指标的超标倍数列于下表,试用模糊等价关系进行分类。
解:写成样品的观测数据矩阵:
按绝对值减数法计算模糊关系,取c=0.1得:
r11=r22=⋯=r55=1
r12=1-0.1(|x11-x21|+|x12-x22|+|x13-x23|+|x14-x24|)=1-0.1(|5-2|+|5-3|+|3-4|+|2-5|)=0.1
同理可得r13=0.8,⋯,r54=0.6。
由此得到模糊关系:
显然 满足自反性、对称性,但不满足传递性。
满足自反性、对称性,但不满足传递性。
可以验证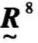 =
=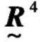 ○
○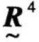 =
=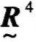 ,故
,故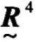 =
=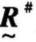 为模糊等价关系。
为模糊等价关系。
若取λ=0.5得:
从而得分类结果:{x1,x3,x4,x5},{x2}两类。
取λ=0.8得:
从而得分类结果:{x1,x3},{x2},{x4},{x5}四类。
取λ=1得:
从而得分类结果:{x1},{x2},{x3},{x4},{x5}五类。
由此得动态聚类图:
相关文章

声音的传播介质有空气、液体和固体,它们分别称为空气声、液体声和固体声等。人类生活在一个声音的环境中,通过声音进行交谈、表达思想感情,以及进行各种活动。这些为人们生活和工作所不需要的声音称为噪声。从物理现象判断,一切无规律的或随机的声信号叫噪声;噪声的判断还与人们的主观感觉和心理因素有关,即一切不希望存在的干扰声都叫噪声。......
2025-09-30

聚类分析的算法可以分为划分的方法、层次的方法、基于密度的方法、基于网格的方法、基于模型的方法等,其中,前两种方法最常用。图4-6层次聚类法示例4.基于网格的方法基于网格的聚类方法采用一个网格数据结构,把对象空间量化为有限数目的单元,形成了一个网格结构。......
2025-09-30

如果把少量石灰和陈醋混在一起,你会发现醋的酸味很快消失了。凡是腐烂的植物,无论树叶、苔藓,还是芦苇、老树干,都会产生一种有一点儿苦味的物质,我们称之为“酸”。酸对植物的生长非常不利。最明显的例子是沼泽地,那里含有的酸性物质就是过量的,非常不适于种植各类农作物,只有无用的芦苇和莎草艰难地生长。石灰恰好能改善这种酸性环境,能在沼泽和潮湿的草甸上创造奇迹。......
2025-09-30

在正常电器的载流件彼此间均有作用力的情况下,电流值通常为正常工作电流的10~100倍,在大电网中可达100 000 A。因此,短路时的电动力异常大,在其作用下,载流件和与之连接的结构件、绝缘件,如支持瓷瓶、引入套管和跨接线等,均可能发生形变或损坏,而且载流元件在短路时的严重发热还将加重电动力的破坏作用。......
2025-09-29

因此,在潜水面以上常形成毛细水带。图1-3各种形态的水在岩层中的分布气态水、结合水、毛细水和重力水在地壳最表层岩土中的分布有一定的规律性。当在松散岩土中开始挖井时,岩土是干燥的,但是实际上存在着气态水和结合水;继续向下挖,发现岩土潮湿,说明岩土中有毛细水存在;再向下掘进,便开始有水渗入井中,并逐渐形成地下水面,这就是重力水。......
2025-09-30

已有的研究工作表明,系统发电机的惯性时间常数、调速器参数、负荷的相关参数等对频率特性曲线均具有一定的敏感性和调整作用,通过参数辨识和调整这些参数,可以使仿真轨迹更接近于实测轨迹[5~7],进而得到更为符合电力系统运行实际情况的仿真结果。......
2025-09-29

美国法典没有规定以哪一时间作为计算被征收不动产价值的时间标准。究竟以哪一日期为征收之日,美国法典并未提供哪怕是倾向性的指引。当然,有学者认为,美国法典没有列举事实上存在的另一种征收种类,即反向征收,也称为驱逐性征收。《美国法典》第40卷第3114节规定了“快速征收程序”,[15]即在某些情况下,允许政府在法院对征收做出判决前“宣告征收”某些财产,随即占有被征收的财产。反向征收中的情形。......
2025-09-29

(一)铂钴标准比色法该方法用氯铂酸钾与氯化钴配成标准色列,与水样进行目视比色确定水样的色度。规定每升水中含1mg铂和0.5mg钴所具有的颜色为1个色度单位,称为1度。因氯铂酸钾价格贵,故可用重铬酸钾代替氯铂酸钾,用硫酸钴代替氯化钴,配制标准色列。该方法适用于清洁的、带有黄色色调的天然水和饮用水的色度测定。......
2025-09-30
相关推荐