首页理论教育环境监测：直线相关和回归的变量关系及线性关系分析

环境监测：直线相关和回归的变量关系及线性关系分析

2023-11-23 理论教育版权反馈

【摘要】：（一）相关和直线回归方程变量之间的关系有两种主要类型：1.确定性关系例如：欧姆定律I＝U/R，已知三个变量中任意两个就能按公式求出第三个变量。[例]用分光光度法测酚得到下表所列数据，试求吸光度和质量浓度（ρ）的直线回归方程。直线回归方程为：＝3.4x＋0.013由此得到酚的吸光度与质量浓度的关系图，如图10-2所示。求其线性关系如何，并作显著性检验。

在环境监测中经常要了解各种参数之间是否有联系，例如：BOD和TOC都是代表水中有机污染的综合指标，它们之间是否有关；又如：在水稻田施农药，水稻叶上农药残留量与施药后时间之间是否有关。下面将介绍怎样判断各参数之间的联系。

（一）相关和直线回归方程

变量之间的关系有两种主要类型：

1.确定性关系

例如：欧姆定律I＝U/R，已知三个变量中任意两个就能按公式求出第三个变量。

2.相关关系

有些变量之间既有关系但又无确定性关系，称为相关关系，它们之间的关系式叫回归方程，最简单的直线回归方程为：

其中a、b为常数，当x为xi时，实际y值在按计算所得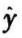左右波动。

上述回归方程可根据最小二乘法来建立。即首先测定一系列x1、x2、⋯、xn和相对应的y1、y2、⋯、yn，然后按下式求常数a和b。

[例]用分光光度法测酚得到下表所列数据，试求吸光度（A）和质量浓度（ρ）的直线回归方程。

解：设质量浓度数值为x，吸光度为y。

直线回归方程为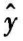：＝3.4x＋0.013

由此得到酚的吸光度与质量浓度的关系图，如图10-2所示。

图10-2 酚的吸光度与质量浓度的关系图

（二）相关系数及其显著性检验

相关系数是表示两个变量之间关系的性质和密切程度的指标，符号为γ，其值为﹣1～＋1，公式为：

x与y的相关关系有如下几种情况：

（1）若x增大，y也相应增大，称x与y成正相关，此时0＜γ＜1；若γ＝1，称完全正相关。图10-3是正相关的两种图形。(www.chuimin.cn)

（2）若x增大，y相应减小，称x与y成负相关，此时，﹣1＜γ＜0；当γ＝﹣1时，称完全负相关。图10-4是负相关的两种图形。

（3）若y与x的变化无关，称x与y不相关。此时γ＝0。图10-5是不相关的四种图形。

图10-3 正相关的两种图形

图10-4 负相关的两种图形

图10-5 不相关的四种图形

若总体中x与y不相关，在抽样时由于随机误差，可能计算所得γ≠0。所以应检验γ值有无显著性意义，方法如下：

①求出γ值。

②按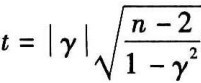求出t值，n为变量配对数，自由度n＇＝n－2。

③查t值表（一般单侧检验）。

若t＞t0.01（n＇），P＜0.01，γ有非常显著性意义；若t＜t0.1（n＇），P＞0.1，γ无显著性意义。

[例]用二乙氨基二硫代甲酸银分光光度法测砷时得到下表所列数据。求其线性关系如何，并作显著性检验。

解：设砷的质量为xμg，吸光度为y。

从γ＝0.9993可知x与γ几乎成完全正相关。

显著性检验：

因本例是正相关，不会出现负相关，用单侧检验，查表得t0.01（6）＝3.14

t＝65.43＞＞3.14＝t0.01（6）

所以正相关有非常显著性意义。