在实验室质量考核中,对标准样品的实际测量均值与其保证值之间的差异是由抽样误差引起的,还是确实存在本质的差别,可用计算t值和查t值表的方法来判断两均值之差属于抽样误差的概率有多大,即对这些差异进行“显著性检验”,简称“t检验”,当抽样误差的概率较大时,两均值的差异很可能是抽样误差所致,亦即两均值无显著性差异;如其概率很小,即此差异属于抽样误差的可能性很小,因而两均值有显著性差异。......
2023-11-23
监测数据按数理统计进行处理及表述,注意以下问题。
(一)数据修约规则
在同一份报告中应按规定保留有效数字位数,计算的数据需要修约时,应遵守下列规则:四舍六入五考虑,五后非零则进一,五后皆零视奇偶,五前为偶应舍去,五前为奇则进一。
(二)可疑数据的取舍
与正常数据不是来自同一分布总体、明显歪曲实验结果的测量数据,称为离群数据。可能会歪曲实验结果,但尚未经检验断定其是离群数据的测量数据,称为可疑数据。
在数据处理时,必须剔除离群数据以使测量结果更符合客观实际。正确数据总有一定的分散性,如果人为地删去一些误差较大但并非离群的测量数据,由此得到精密度很高的测量结果并不符合客观实际。因此对可疑数据的取舍必须遵循一定的原则。
测量中若发现明显的系统误差和过失,则由此产生的数据应随时剔除。而可疑数据的取舍应采用统计方法判别,即离群数据的统计检验。检验的方法很多,现介绍最常用的两种。
1.狄克松(Dixon)检验法
此法适用于一组测量值的一致性检验和剔除离群值,本法中对最小可疑值和最大可疑值进行检验的公式因样本容量(n)不同而异,检验方法如下:
(1)将一组测量数据按从小到大顺序排列为x1、x2、⋯、xn,x1和xn分别为最小可疑值和最大可疑值。
(2)按表10-6计算式求Q值。
(3)根据给定的显著性水平(α)和样本容量(n),从表10-7查得临界值(Qα)。
(4)若Q≤Q0.05,则可疑值为正常值;若Q0.05<Q≤Q0.01,则可疑值为偏离值;若Q>Q001,则可疑值为离群值。
表10-6 狄克松检验法Q值计算式
表10-7 狄克松检验法临界值(Qa)
续表
[例]一组测量值从小到大顺序排列为:14.65、14.90、14.90、14.92、14.95、14.96、15.00、15.01、15.01、15.02。检验最小值14.65 和最大值15.02 是否为离群值。
解:检验最小值x1=14.65,n=10,x2=14.90,xn-1=15.01,则:
查表10-7,当n=10,给定显著性水平α=0.01时,Q0.01=0.597。
Q>Q0.01,故最小值14.65为离群值,应予剔除。
检验最大值xn=15.02,有:
查表10-7可知,Q0.05=0.477。
Q<Q0.05,故最大值15.02为正常值。
2.格鲁布斯(Grubbs)检验法
此法适用于检验多组测量值均值的一致性和剔除多组测量值中的离群均值;也可用于检验一组测量值的一致性和剔除一组测量值中的离群值,方法如下:
(1)有l组测量值,每组n个测量值的均值分别为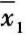
 、⋯、
、⋯、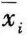 、⋯、
、⋯、 ,其中最大均值记为
,其中最大均值记为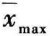 ,最小均值记为
,最小均值记为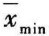 。
。
(2)由l个均值计算总均值(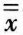 )和标准偏差(
)和标准偏差(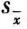 ):
):
(3)可疑均值为最大均值(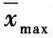 )时,按下式计算统计量(T):
)时,按下式计算统计量(T):
可疑均值为最小均值(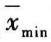 )时,按下式计算统计量(T):
)时,按下式计算统计量(T):
(4)根据测量值组数和给定的显著性水平(α),从表10-8查得临界值T α)。
(5)若T≤0.05,则可疑均值为正常均值;若T0.05<T≤T0.01,则可疑均值为偏离均值;若T>T0.01,则可疑均值为离群均值,应予剔除,即剔除含有该均值的一组数据。
表10-8 格鲁布斯检验法临界值(Tα)
[例 10个实验室分析同一样品,各实验室5 次测量的平均值按从小到大的顺序排列为:4.41、4.49、4.50、4.51、4.64、4.75、4.81、4.95、5.01、5.39,检验最大均值5.39是否为离群均值。
解: 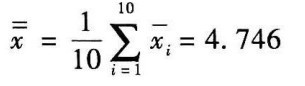
则统计量
当l=10、给定显著性水平α=0.05时,查表10-8得临界值T0.05=2.176。
因T<T0.05,故5.39为正常均值,即均值为5.39的一组测量值为正常值。
(三)监测结果的表述
1.用算术平均值( )表示测量结果与真值的集中趋势
)表示测量结果与真值的集中趋势
测量过程中排除系统误差和过失后,只存在随机误差,根据正态分布的原理,当测定次数无限多(n→∞)时的总体均值(μ)应与真值(xt)很接近,但实际测量次数有限。因此样本的算术平均值是表示测量结果与真值的集中趋势以表达监测结果的最常用的方式。
2.用算术平均值和标准偏差表示测量结果的精密度(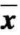 ±s)
±s)
算术平均值代表集中趋势,标准偏差表示离散程度。算术平均值代表性的大小与标准偏差的大小有关,即标准偏差大,算术平均值代表性小,反之亦然,故而监测结果常以( ±s)表示。
±s)表示。
3.用( ±s,CV)表示结果(www.chuimin.cn)
±s,CV)表示结果(www.chuimin.cn)
标准偏差大小还与所测均值水平或测量单位有关。不同水平或单位的测量结果之间,其标准偏差是无法进行比较的,而变异系数是相对值,故可在一定范围内用来比较不同水平或单位测量结果之间的差异。例如:用镉试剂分光光度法测量镉,当镉质量浓度小于0.1mg/L时,标准偏差和变异系数分别为7.3%和9.0%。
(四)均值置信区间和“t”值
均值置信区间是考察样本均值( )与总体均值(μ)之间的关系,即以样本均值代表总体均值的可靠程度。从正态分布曲线可知,68.26%的数据在μ±σ区间,95.44%的数据在μ±2σ区间等。正态分布理论是从大量数据中得出的。当从同一总体中随机抽取足够量的大小相同的样本,并对它们测量得到一批样本均值,如果原总体是正态分布,则这些样本均值的分布将随样本容量(n)的增大而趋向于正态分布。
)与总体均值(μ)之间的关系,即以样本均值代表总体均值的可靠程度。从正态分布曲线可知,68.26%的数据在μ±σ区间,95.44%的数据在μ±2σ区间等。正态分布理论是从大量数据中得出的。当从同一总体中随机抽取足够量的大小相同的样本,并对它们测量得到一批样本均值,如果原总体是正态分布,则这些样本均值的分布将随样本容量(n)的增大而趋向于正态分布。
样本均值的均值符号为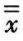 ,样本均值的标准偏差符号为
,样本均值的标准偏差符号为 。标准偏差(s)只表示个体变量值的离散程度,而均值标准偏差是表示样本均值的离散程度。
。标准偏差(s)只表示个体变量值的离散程度,而均值标准偏差是表示样本均值的离散程度。
均值标准偏差的大小与总体标准偏差成正比,与样本容量的平方根成反比:
由于总体标准偏差不可知,故只能用样本标准偏差来代替,即
这样计算所得的均值标准偏差仅为估计值,均值标准偏差的大小反映抽样误差的大小,其数值越小则样本均值越接近总体均值,以样本均值代表总体均值的可靠性就越大;反之,均值标准偏差越大,则样本均值的代表性越不可靠。
样本均值与总体均值之差对均值标准偏差的比值称为t值:
移项 
根据正态分布的对称性特点,应写成:
式中右面的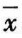 、s和n通过测量可得,t与样本容量(n)和置信度有关,而后者可以直接要求指定。t值见表10-9。由表可知,当n(n'=n-1)一定,要求置信度越大则t值越大,其结果的数值范围越大。而置信度一定时,n越大t值越小,结果的数值范围越小。置信度不是一个单纯的数学问题,置信度过大反而无实用价值,例如:100%的置信度,则数值范围的区间为[﹣∞,+∞]。通常采用90%~95%置信度[P(双侧概率)对应为0.10~0.05]。
、s和n通过测量可得,t与样本容量(n)和置信度有关,而后者可以直接要求指定。t值见表10-9。由表可知,当n(n'=n-1)一定,要求置信度越大则t值越大,其结果的数值范围越大。而置信度一定时,n越大t值越小,结果的数值范围越小。置信度不是一个单纯的数学问题,置信度过大反而无实用价值,例如:100%的置信度,则数值范围的区间为[﹣∞,+∞]。通常采用90%~95%置信度[P(双侧概率)对应为0.10~0.05]。
表10-9 t值表
续表
[例]测定某废水中氰化物浓度得到下列数据:n=4,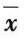 =15.30(mg/L),s=0.10(mg/L),求置信度分别为90%和95%时的置信区间。
=15.30(mg/L),s=0.10(mg/L),求置信度分别为90%和95%时的置信区间。
解:n'=n-1=3。
置信度为90%时,查表得t=2.35,
≈15.30±0.12(mg/L)
即90%的可能为15.18~15.42mg/L。
同理:置信度为95%时,查表得t=3.18,
≈15.30±0.16(mg/L)
即95%的可能为15.14~15.46mg/L。
[例]有一氯化物的标准水样,质量浓度为110mg/L,以银量法测定5次,测得质量浓度为112mg/L、115mg/L、114mg/L、113mg/L、115mg/L,求:算术平均值、几何平均值、中位数、绝对误差、相对误差、绝对偏差、平均偏差、极差、样本的差方和、方差、标准偏差和相对标准偏差(变异系数)。
几何平均值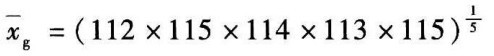
=113.8(mg/L)
中位数:114(mg/L)
以xi为112(mg/L),xt为110(mg/L)为例:
绝对误差xi-xt=112-110
=2(mg/L)
绝对偏差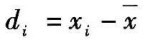
=112-113.8
=-1.8(mg/L)
平均偏差
=1.04(mg/L)
极差R=115-112=3(mg/L)
样本差方和S =(112-113.8)2+(115-113.8)2+(114-113.8)2+(113-113.8)2+(115-113.8)2
=(﹣1.8)2+(1.2)2+(0.2)2+(﹣0.8)2+(1.2)2
=6.8[(mg/L)2]
样本方差
=1.7[(mg/L)2]
样本标准偏差
=1.3(mg/L)
样本相对标准偏差(变异系数) =1.1%
=1.1%
有关环境监测的文章

在实验室质量考核中,对标准样品的实际测量均值与其保证值之间的差异是由抽样误差引起的,还是确实存在本质的差别,可用计算t值和查t值表的方法来判断两均值之差属于抽样误差的概率有多大,即对这些差异进行“显著性检验”,简称“t检验”,当抽样误差的概率较大时,两均值的差异很可能是抽样误差所致,亦即两均值无显著性差异;如其概率很小,即此差异属于抽样误差的可能性很小,因而两均值有显著性差异。......
2023-11-23

我国如何逐步和国际接轨?印染厂上游水质如下:pH=7.3,水温<33℃,水面无明显泡沫、油膜及漂浮物,天然色度<15度,臭和浊度均为一级,DO=5.5mg/L,BOD5=2.6mg/L,COD=5.5mg/L,ρ(挥发酚)=0.004mg/L,ρ(氰化物)=0.02mg/L,ρ=0.005mg/L,ρ(总Hg)=0.0001mg/L,ρ(总Cd)=0.005mg/L,ρ=0.008mg/L,ρ[Cr]=0.015mg/L,ρ=0.04mg/L,ρ(石油类)=0.2mg/L,ρ(硫化物)=0.01mg/L,大肠菌群浓度=800个/L。......
2023-11-23

甲烷不参与光化学反应,因此,测定非甲烷烃对判断和评价空气污染具有实际意义。测定总烃和非甲烷烃的主要方法有:气相色谱法、光电离检测法等。以氮气为载气的气相色谱法测定总烃和非甲烷烃的流程示于图3-29。以上两质量浓度之差即为非甲烷烃质量浓度。但是,所检测的非甲烷烃是指C4以上的烃,而气相色谱法检测的是C2以上的烃。......
2023-11-23

现场采集的土壤样品经核对无误后,进行分类装箱,运往实验室加工处理。图5-5 土壤样品的四分法示意图测定挥发性或不稳定组分,如挥发酚、氨氮、硝酸盐氮、氰化物等,需用新鲜土样。(二)样品管理土壤样品管理包括土样加工处理、分装、分发过程中的管理和土样入库保存管理。在保存期内,应定期检查土样保存情况,防止霉变、鼠害和土壤样品标签脱落等。......
2023-11-23

浸出毒性试验采用规定方法浸出水溶液,然后对浸出液进行分析。每种样品做两个平行浸出毒性试验,每瓶滤液对欲测项目平行测定两次,取算术平均值报告结果;对于含水污泥样品,其滤液也必须同时加以分析并报告结果;试验报告中还应包括被测样品的名称、来源、采集时间、样品粒度级配情况,试验过程中出现的异常情况,浸出液的pH、颜色、乳化和相分层情况,试验过程的环境温度及其波动范围、条件改变及其原因。......
2023-11-23

(一)污染源分布及排放情况通过调查,将监测区域内的污染源类型、数量、位置、排放的主要污染物及排放量调查清楚,同时还应了解所用原料、燃料及其消耗量。此外,对于监测区域以往的监测资料等也应尽量收集,供制订监测方案参考。......
2023-11-23

对26个原苏东国家的民主转型案例的测量分为条件和结果。特别要指出的是,转型前的经济状况用转型开始那一年的人均国内生产总值和每升石油的国内生产总值产出来表示,这两个变量的数据均来源于世界银行发展指数。[28]表4-1结果变量和条件变量的设定......
2023-08-16
相关推荐