傅里叶光学原理及系统设计-光信息处理

2023-11-23 理论教育版权反馈

【摘要】：随着科学技术的飞速发展，光学系统设计在近40年的发展过程中，经历了由人工计算像差、人工修改结构参数进行设计到使用电子计算机和光学自动设计程序进行设计的巨大飞跃。目前，计算机辅助设计CAD在现代光学系统设计中应用已相当普遍，人们已经研制出功能比较完善的光学设计CAD软件。利用上面所讨论的光学设计自动设计方法，采用目前国际上流行的光学设计软件ZEMAX和Code V，就可以对光信息处理光学系统进行设计，使其满足使用要求。

随着科学技术的飞速发展，光学系统设计在近40年的发展过程中，经历了由人工计算像差、人工修改结构参数进行设计到使用电子计算机和光学自动设计程序进行设计的巨大飞跃。目前，计算机辅助设计CAD在现代光学系统设计中应用已相当普遍，人们已经研制出功能比较完善的光学设计CAD软件。利用光学设计CAD软件中的光学自动设计模块，人们不仅节省了大批劳动力，缩短了设计周期，同时也使人们有可能设计出质量更高、结构更简单的新型现代光学系统。

在光学自动设计中，我们把对系统的全部要求，根据它们和结构参数的关系不同重新划分成两大类。

第一类是不随系统结构参数改变的常数。如：物距L、孔径高H或孔径角正弦sinU、视场角ω或物高y、入瞳或孔径光阑的位置，以及轴外光束的渐晕系数K+、K-等。在计算和校正光学系统像差的过程中这些参数永远保持不变，它们是和自变量（结构参数）无关的常量。

第二类是随结构参数改变的参数。它们包括代表系统成像质量的各种几何像差或波像差。同时也包括某些近轴光学特性参数，例如焦距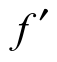 pagenumber_ebook=353,pagenumber_book=337 、放大率β、像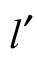距、出瞳距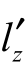等。为了简单起见，今后我们把第二类参数统称为像差，用符号F1、···、Fm 代表；系统的结构参数用符号x1、···、xn 代表。两者之间的函数关系可用下列形式表示：

f1、···、fm 分别代表像差F1、···、Fm 与自变量x1、···、xn 之间的函数关系。式（7-14）是一个十分复杂的非线性方程组，称为像差方程组。我们把像差和结构参数之间的函数关系，近似用下列线性方程式来代替：

式（7-16）称为像差线性方程组，用它来近似代替像差方程组（7-14）。这就是光学自动设计的基本出发点。为了简单，我们用矩阵形式来表示上述方程组，设：

这样像差线性方程组的矩阵形式为

求解上述线性方程组，得到一组解Δx，然后用一个小于1的常数p乘Δx得到：

按　Δxp对原系统进行修改，当p足够小时，总可以获得一个比原系统有所改善的新系统。因为当p足够小时，像差线性方程组能近似反映系统的像差性质。把新得到的系统作为新的原始系统，重新建立像差线性方程组进行求解。这样不断重复，直到各种像差符合要求为止。这就是目前绝大多数光学自动设计程序所采用的主要数学过程。

目前国际上主流的光学设计软件都是采用阻尼最小二乘法的光学自动设计程序。对于像差线性方程组，当像差数m大于自变量数n的时候，方程组（7-17）是一个超定方程组，它不存在满足所有方程式的准确解，只能求它的近似解——最小二乘解。下面先介绍最小二乘解的定义。

首先定义一个函数组φ(φ1,…,φm)，它们的意义如以下公式所示：

式中，φ1、···、φm 称为像差残量，写成矩阵形式为

取各像差残量的平方和构成另一个函数Φ(Δx)：(www.chuimin.cn)

Φ(Δx)在光学自动设计中称为评价函数，能够使Φ(Δx)=0的解（即φ1=···=φm =0），就是像差线性方程组的准确解。当m ＞n时，它实际上是不存在的。如果改为求Φ(Δx)的极小值解，作为方程组（7-17）的近似解，称为像差线性方程组的最小二乘解。因为评价函数Φ(Δx)越小，像差残量越小，越接近我们的要求。将φ代入评价函数得

根据多元函数的极值理论，Φ(Δx)取得极小值解的必要条件是一阶偏导数等于零，即

这是一个新的线性方程组，它的方程式的个数和自变量的个数都等于n 。这个方程组称为最小二乘法的法方程组。

运用矩阵求导规则求Φ(Δx)的一阶偏导数

上式即为有n个方程式n个自变量的最小二乘法的法方程组。只要方阵ATA为非奇异矩阵，即它的行列式值不等于零，则逆矩阵(AT A)-1存在，方程式（7-19）有解，解的公式为

它就是评价函数中（Δx）的极小值解，也就是像差线性方程组（7-14）的最小二乘解。这种求超定方程组最小二乘解的方法称为最小二乘法。要使（ AT A）非奇异，则要求方程（7-17）的系数矩阵A不产生列相关，即像差线性方程组中不存在自变量相关。在光学设计中，由于像差和结构参数之间的关系是非线性的，同时在比较复杂的光学系统中作为自变量的结构参数很多，很可能在若干自变量之间出现近似相关的现象。这就使矩阵AT A的行列值接近于零，AT A接近奇异，按最小二乘法求出的解很大，大大超出了近似线性的区域，用它对系统进行修改，往往不能保证评价函数Φ(Δx)的下降，因此必须对解向量的模进行限制。因此，我们改为求下列函数的极小值解

这样做的目的是，既要求评价函数Φ(Δx)下降，又希望解向量的模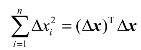 pagenumber_ebook=356,pagenumber_book=340 不要太大。经过这样改进的最小二乘法，称为阻尼最小二乘法，常数p称为阻尼因子。上述函数L的极小值解的必要条件为：

或者

上式为阻尼最小二乘法的法方程组，其中I为单位矩阵，p为阻尼因子。解的公式为

以上公式中的逆矩阵(AT A+pI)-1永远存在。在像差线性方程组确定后，即A和FΔ确定后，给定一个p值就可以求出一个解向量Δx。p值越大Δx的模越小，像差和结构参数之间越接近线性，越有可能使Φ(Δx)下降。但是Δx太小时，系统改变不大，Φ(Δx)下降的幅度越小。因此必须优选一个p值，使Φ(Δx)达到最大的下降。采用上述求解方法的光学自动设计称为阻尼最小二乘法。

利用上面所讨论的光学设计自动设计方法，采用目前国际上流行的光学设计软件ZEMAX和Code V，就可以对光信息处理光学系统进行设计，使其满足使用要求。

傅里叶光学原理及系统设计-光信息处理

相关推荐