如森林鸟类群落、草原啮齿动物群落，或者植食性昆虫群落、草原生态系统中的黑线仓鼠+达乌尔鼠兔+达乌尔黄鼠群落。在生产实践中，有害动物的防治、珍稀动物的保护、资源动物的合理利用等问题已不再是单纯依靠种群生态学所能解决的，它还涉及群落生态学或以生态系统为背景的高层次研究。目前动物群落生态学已成为动物生态学的一个重要分支学科。总的来看，我国关于啮齿动物群落生态学研究工作，大多集中在群落结构方面。......
2023-11-22
宁夏啮齿动物地理区系与种间关系的研究成果
【摘要】：对生态位宽度定量的方法很多，以把资源分为若干等级，并调查记录各个物种利用各个资源等级的数值。上述生态位特征的测定，虽然简单，但已被普遍用在群落种间关系的分析中。（二）群落内种间关系群落内各物种之间的相互关系是群落生态学研究中的一个重要内容，因为种间关系是群落赖以生存的基础。当然，要全面地、定量地研究群落网络结构中各物种之间的关系
（一）生态位
1.生态位（ecological niche）的概念生态位最早是格林尼尔（Grinell）在1917年应用的，以表示对栖息地再划分的空间单位，换言之，即生物出现在环境中的空间范围。1927年Elton提出，生态位是有机体在群落中的机能作用和地位（functional role and position），使生态位的概念得到了扩展。之后，哈里森（1958）把环境因素数值化，并把环境变量的多维概念引入生态位中，认为生态位是群落中每一物种需要的特殊环境（物理的生物的复合体）及其独特功能，形成“超体积生态位”（hypervolume niche）的概念。能够为某一物种所栖息的理论上最大空间，即为基础生态位（fundamental niche）。但实际是很少有一种动物能全部占据其基础生态位，当竞争存在时，此一物种必然只能占据基础生态位的一部分空间，这一空间就称为实际生态位（realized niche）。参与竞争的种越多，该种占有的实际生态位的空间就越小。
2.生态位宽度（niche breadth）生态位宽度是生物利用资源多样性的一个指标。在现有资源谱中，仅能利用其一小部分的生物，就称为狭生态位的，能利用其很大部分的，则称为广生态位的。对生态位宽度定量的方法很多，以把资源分为若干等级，并调查记录各个物种利用各个资源等级的数值。
（1）Shannon-weiner的生态位宽度指标（Bi）
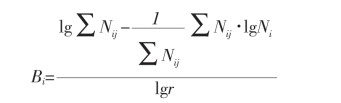
公式中，Bi为第i个物种的生态位宽度，Ni为第i个物种利用第j个资源的数值，r为生态位资源等级数。当物种利用资源序列的全部等级，并且在每个等级上利用资源相等（即Ni=N2=……Nr）时，该物种生态位宽度最大；如果该物种利用资源序列中的1个等级，则该物种的生态位宽度最小，Bmin=0。
（2）Levins（1968）的生态位宽度指数（Bi）生态位宽度是物种利用或趋于利用所有可利用资源状态而减少种内个体相遇的程度，或为生态专一性的倒数。物种的生态位宽度越大，其对环境的适应性就越强。Levin（1968）的生态位宽度指数公式为：
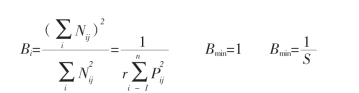
公式中，Pij为第i个物种数量在第j个群落中的组成比，i=1、2……群落的物种数，j=1、2……n；n为群落总数；0<Bi≤1，Bi越趋向1，物种的生态位宽度越大；Bmax为生态位宽度的最大值，Bmin为生态位宽度的最小值；Bi、r同上。
（3）生态位相似性比例（Proportional similarity）群落的相似性比例表示了群落中两物种之间的分布和利用资源的相似程度。Cowell和Futuyma（1971）生态位相似性比例（Ps）
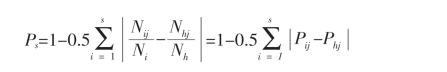
式中，Ps为i物种和h物种之间的比例相似性，Nij、Nhj为i物种和h物种在j资源等级中出现的数值，Ni、Nh为物种i和h在所有资源中出现的数值，S为各群落中相对应的物种数，Pij和Phj为物种i和h在第j个群落中的组成比。
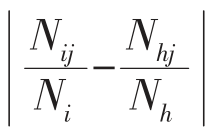为绝对值，反映了两个物种之间利用资源比例之差。该指数的取值范围是0≤Ps≤1，0表示完全不相似，1表示100%的相似。
3.生态位重叠（Niche overlap）生态位重叠是两个物种在其与生态因子联系上的相似性，是种群对相同资源的共同利用，或者是共有的生态空间资源区域。
（1）Levins的生态位重叠指数（Ns）
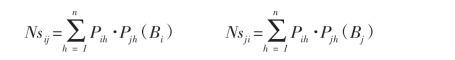
公式中，Nsij和Nsji分别为物种i对物种j和物种j对物种i的生态位重叠，Pjh和Pjh为物种i和j在第h个群落中的组成比，Bi和Bj为物种i和物种j的生态位宽度。
当两物种在任何一资源都不重叠时，Nsij=Nsji=0；当两物种利用资源等级完全重叠时，i种对j种的重叠正好等于i种的生态位宽度，即Nsij=Bi；j种对i种的重叠正好等于j种的生态位宽度，即Nsji=Bj；当Bi大于Bj时，虽然两物种生态位重叠部分的绝对值相同，但i物种对j种的重叠大于j种对i种的重叠。
（2）Hutchinson（1978）的生态位重叠指数（C）Hutchinson的生态位重叠指数考虑了在群落序列中资源不等价的问题。
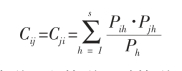
公式中，Cij、Cji分别为物种i对物种j和物种j对物种i的生态位重叠，j、S、Pjh和Pjh与Levins的生态位重叠指数公式中的相同，Ph位资源系列第j等级的资源占所有可利用资源的比例。
（3）Shannon-weiner的生态位重叠指数（C）
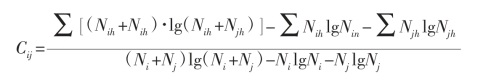
公式中的符号定义与上述公式相同。取值范围：0≤Cij≤1。
4.生态位分离和性状替换
（1）生态位分离（niche separation）是指两个物种在资源序列上利用资源的分离程度。假定两个物种各自在连续资源序列上的资源利用曲线为一钟形曲线，设它们的平均分离度为d，各自的变异度为W（用68%的标准差表示），则生态位分离的程度（NP）为
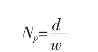
当生态位充分分离时，d/w值大；当生态位高度重叠时，d/w值小。(www.chuimin.cn)
（2）性状替换（character displacement）性状替换可以理解为由于竞争造成生态分离的证明。指两个亲缘关系密切的物种若分布在不同的区域时，它们的特征往往十分相似，甚至难以区别。但在同一区域分布时，它们之间的差异就明显，彼此之间必然出现明显的生态分离。这就会出现一个或几个特征的相互替换。这种性状替换现象是近缘种之间相互激烈竞争的结果。
上述生态位特征的测定，虽然简单，但已被普遍用在群落种间关系的分析中。应用这些测度值时，必须注意它们的生态学含义及其变动范围；并且在比较群落中不同物种之间的生态位特征时，应该选择同一种计算方法，以保证测度值的可比性。
（二）群落内种间关系
群落内各物种之间的相互关系是群落生态学研究中的一个重要内容，因为种间关系是群落赖以生存的基础。生态系统内的能流与物质循环是群落的主要功能，这种功能归根到底是物种间取食与被食的关系在起作用；群落的分布格局和发展演替在很大程度上也受着种间关系，特别是种间竞争的影响。显然，只有把群落内的物种间关系弄清楚了，甚至可以定量地描述了，才能更深刻地认识群落的营养结构和整体功能，为群落的动态预测和科学管理奠定扎实的基础。当然，要全面地、定量地研究群落网络结构中各物种之间的关系是困难的，为此，仍然不得不采用传统的种群生态学的方法，只是在阐述有欠理论时，尽可能说明种间关系对整个群落的影响和作用。
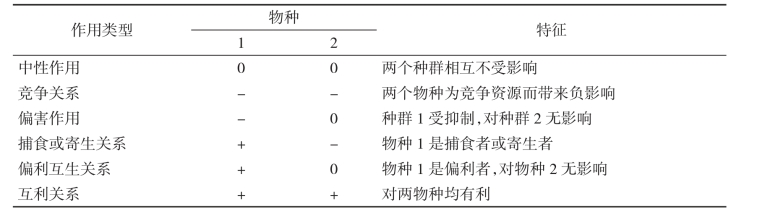
1.种间关系的基本形式两个物种间关系的基本形式有6种（表1-2）。若用“+”表示有利，用“-”表示不利，用“0”表示无影响。则表示方法简单、明确，可用以定义不同物种间关系的本质特征。
两种之间相互关系的形式可能在不同条件下发生转化，或者在生活史的不同阶段有所不同。如两个物种在某一时间是寄生关系，而在另一时间成为偏利作用，到后来可能成为完全的中性作用。研究简化了的群落，或进行室内实验，可以帮助我们分离出各种不同的相互关系类型，并可能进行定量研究，进而演绎出数学模型，有利于分析一些难以彼此分开的因素。
表1-2 两个物种间相互作用的类型
2.竞争排斥原理在自然界里，常常可以见到具有相似环境要求的两个物种，为了争取有限的食物、空间等环境资源，大多不能长期共存，除非环境改变了竞争的平衡，或是两个物种发生了生态分离（ecological separation），否则两者之间的生存竞争迟早会导致竞争能力差的物种的灭亡。这种现象被称为竞争排斥原理（principle of competitive exclusion）。
竞争排斥原理首先由Gouse（1934）用实验方法证明，所以又称为高斯假说（Gouse＇hypothesis）。高斯用两种分类上和生态上都很近的草履虫，即双核草履虫（Paramecium aurelia）和大草履虫（P．caudatum），以一种杆菌（Bacillus pyacyaneus）作为饲料进行实验。当单独培养时，两种草履虫都表现为“S”型增长曲线。但当把两种草履虫放在一起培养时，开始两个种都有增长，但双核草履虫增长较快，并在16天后仍然生存，而大草履虫完全灭亡。据分析，两种草履虫都没有分泌有害物质，显然是由于竞争共同的食物而排斥了其中的一种。
3.洛特卡—沃尔泰勒（Lotka-voltcrra）模型及其生态学含义Lotka-voltcrra模型是描述种间竞争的模型。其基础是逻辑斯谛模型。
当物种甲和物种乙单独存在时，其增长过程可以用逻辑斯谛方程表示：
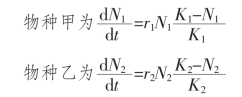
若两个物种在同一空间中生长，那么每一物种的增长率除决定于本物种的密度和内禀增长率外，与种群尚未利用的空间（K-N）/K有很复杂的关系。如对物种甲而言，在环境容纳量的K1值中，除有本种已经积聚的密度N1以外，还有物种乙（N2）也有时利用K的空间。那么，怎样来描述物种乙的影响呢?可以把物种甲的环境比喻为一个盒子，它能容纳K1个物种甲的个体（小方块）。盒子的空间同样能为竞争者物种乙占据。同样的资源，对不同种的容纳量可能不同，在大多数情况下，一个个体所占的“空间体积”对物种甲和乙不会相等。例如，物种乙可能个体较大，需要较大的空间。可以算出二者的当量，如
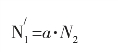
a表示a个N2个体所占的K1空间，相当于1个N1个体所占的空间。在K1空间中，每有1个N2个体，其占有的空间相当于10个N1个体，即
在此，“α”可以称为物种乙对物种甲的竞争系数（compitiive coefficient），它表示在物种甲的环境中，每存在一个物种乙的个体对物种甲所产生的效应。
当α＝1时，表示一个N2所占的空间体积与一个N1相等；
当α＜1时，表示一个N2个体所占的空间体积比一个N1的大；
当α＞l时，表示一个N2个体所占的空间体积比一个N1的小。
假定在任何密度下，两个种的竞争系数保持稳定，则物种甲的Lotka-voltcrra竞争方程是：
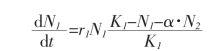
同理，对物种甲来说，若物种乙的竞争系数是β，即有
则物种乙的Lotka-voltcrra竞争方程是
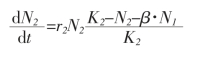
有关宁夏啮齿动物地理区系区划及分类管理的文章
- 详细阅读
-
宁夏啮齿动物地理区系的种群特征详细阅读
一般来说，自然种群有三个基本特征：①空间特征，即种群具有一定的分布区域。（一）种群密度种群密度通常以单位空间的个体数或生物量来表示。在特定环境条件下种群实际上的出生率称为实际出生率。有指整个种群的平均死亡率，也有处于不同发育阶段群体的特殊死亡率。故有人认为，鼠类的极高出生率是对极高死亡率的一种适应特点。因此研究种群的数量动态，不能离开种群内的年龄分布状况。......
2023-11-22
-
宁夏啮齿动物地理区系与管理探究详细阅读
更由于生境内的地形和土壤结构的变化，有的弥散成片状，有的形成带状，亦有的形成岛状，调查时首先应予以注意。每种类型的洞穴至少每季挖掘5个以上，研究其结构和利用的情况。挖掘洞穴时，首先要把洞内的鼠捕尽，以免挖洞时，鼠另挖新洞，从而破坏原洞的结构。捕鼠时，还要注意从洞口内找到雌鼠的洞穴、雄鼠的洞穴和幼鼠的洞穴，更要注意洞穴的结构特征。......
2023-11-22
-
宁夏啮齿动物地理区系管理及分类策略详细阅读
鼢鼠终生营地下生活，因其独特的生活方式和神秘的生活习性，使其成为举世公认的最难治理的害鼠。因各生境下鼢鼠的发生规律、取食特性有所差异，不同生产经营活动的目的不同，加之各种治理措施的适应范围、操作性和成本等不同，因此很难用相同的策略和方法治理所有的鼢鼠危害。（一）林地鼢鼠治理的策略及方法林地鼢鼠治理要根据不同时期、不同林中和不同经营目的，确定治理策略，选择治理方法，制定治理方案。......
2023-11-22
-
宁夏啮齿动物地理区系管理及分类详细阅读
有关宁夏回族自治区林草啮齿动物区系及动物地理区划研究报道资料较少。该危害大区有啮齿动物29种，占宁夏啮齿动物种数的74.36%，隶属9科22属。啮齿动物区系以华北区成分为主体，同时有黄土高原亚区特征。......
2023-11-22
-
宁夏啮齿动物地理区系分类精要详细阅读
有关啮齿目分类学的许多问题至今未能解决。但主要是根据咀嚼肌的结构和附着情况以及牙齿、下颌骨等进行分类。（一）牙齿鼠类牙齿高度特化。牙齿的这一特性，不是鼠类特有的，实际上鼠类这一特性出现相对较晚。这种方式发生在豪猪、天竺鼠、跳鼠等许多类啮齿动物中。然而咀嚼肌演化的三种模式已被多数学者所接受，至少其演化结果在许多啮齿类可以看到。......
2023-11-22
-
宁夏啮齿动物地理区系调查与分类管理详细阅读
性比和年龄组成是种群的特征之一，它与种群动态有密切的关系。种群的性比，随季节和年份变化，调查时应在不同季节和不同年份分别统计，最好将成年体与幼体分开。在统计性成熟个体的性比时，应与种群的繁殖状况和数量动态结合起来综合分析。（二）种群年龄结构动物种群年龄结构，是各种动物种群的主要特征，也是种群生态学研究的基础。对大多数动物来说，体重和体长指标只具有幼年期使用的价值。......
2023-11-22
-
宁夏啮齿动物地理区系与分类管理详细阅读
利用属性对群落进行排序的过程称为正排序；而利用群落对属性进行排序的过程被称为逆排序。前苏联学者Ramensky首先使用一个或两个生态因素的梯度为坐标研究了群落的排序问题。20世纪50年代前后，群落排序方法逐渐成熟。......
2023-11-22
相关推荐