，σl-1（ξ））是σ的一个l维不变子空间，称之为σ循环子空间，记作Zl（ξ；σ）.显然，σ|Zl（ξ；σ）是Zl（ξ；σ）的幂零变换，且幂零指数为l，其矩阵为一个l阶Jordan块矩阵定义10.6 设V是数域F上的n维线性空间，σ是V上的一个线性变换.α1，α2，…......
2023-11-22
计算对称矩阵标准形-高等代数
【摘要】：+x2n=1上的最大值和最小值.10.2.6. 设A是n阶正定矩阵，计算：n重积分.已知：
在第6章中研究了欧氏空间中的对称变换，并得到如下结果：
（1）对称矩阵的特征值一定是实数；
（2）对称矩阵属于不同特征值的特征向量一定是正交的；
（3）对称矩阵一定正交相似（合同）于一个对角形矩阵，或者说对称矩阵一定是可以对角化的.
由此我们可以得到计算对称矩阵A在正交合同之下的标准形的步骤：
（1）计算对称矩阵A的特征值及特征向量；
（2）利用Gram-Schmidt正交化方法把属于同一特征值的特征向量正交化；
（3）把所有求出的特征向量单位化；
（4）用单位化后的特征向量组为列构造正交矩阵O，则该矩阵使得OTAO成为对角形矩阵.
例10.6 用正交变换化二次型f（x1，x2，x3）=3x21+2x22+x23-4x1x2-4x2x3为标准形.
解：二次型的矩阵是
其特征多项式为
f（λ）=（λ+1）（λ-2）（λ-5），
特征值是λ1=-1，λ2=2，λ3=5.
进一步，可解得它们对应的特征向量分别是
把它们正交化并单位化得到
以这三个向量为列构造正交矩阵
则有
作正交变换X=OY，在此变换之下二次型f化为标准形-y21+2y22+5y23.
例10.7 设四阶方阵
求正交矩阵O，使得OTAO是对角阵.
解：首先，计算A的特征多项式
f（λ）=λE-A=λ2（λ-2）2，
从而得到A的四个特征值λ1，2=0和λ3，4=2.
对于特征值λ=0，解齐次线性方程组Ax=0，得到两个线性无关的特征向量
正交化并单位化之后得到(www.chuimin.cn)
对于特征值λ=2，解齐次线性方程组（2E-A）x=0，得到两个线性无关的特征向量
正交化并单位化之后得到
以这四个特征向量为列构造正交矩阵
则有OTAO=diag（0，0，2，2）.
例10.8 利用平面正交变换化双曲线xy=1为标准形式.
解：二次型xy的矩阵是
A的特征多项式是
，特征值是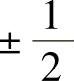
，对应于这两个特征值的特征向量是
单位化之后得到
记正交矩阵
作正交变换X=OX′，其中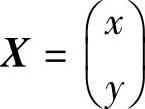
，
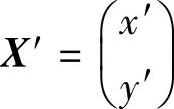，得到双曲线xy=1化为
.
例10.9 判断二次曲面3x2+2y2+z2-4xy-4yz=1的形状.
解：由例10.6可以知道，作正交变换X=OX′，其中
之后，二次曲面的方程变为
由于正交变换不改变曲线的形状，因此，二次曲面是一个单叶双曲面.
习题
10.2.1. 求正交矩阵O，使OTAO成为对角形矩阵，其中A为
10.2.2. 利用正交变换把下列二次型化为标准形.
（1）x21+2x1x2+4x1x3-x22；
（2）2x1x2+6x2x3+2x3x1；
（3）4x21+2x1x2+6x22-8x23.
10.2.3. 把平面二次曲线x2-xy+y2+2x+2y-1=0化为标准形式，并判断它的形状.
10.2.4. 把二次曲面6x2-2y2+6z2+4xz+8x-4y-8z-2=0化为标准形式，并判断它的形状.
10.2.5.若A是n阶对称矩阵，计算：n元函数f（X）=XTAX在n维单位球面x21+x22+…+x2n=1上的最大值和最小值.
10.2.6. 设A是n阶正定矩阵，计算：n重积分
.已知：
有关高等代数的文章
- 详细阅读
-
线性代数9讲-实对称矩阵与正交矩阵详细阅读
（1）若A为实对称矩阵，则①特征值均为实数，特征向量均为实向量.②不同特征值对应的特征向量正交.（即λ1≠λ2ξ1⊥ξ2（ξ1，ξ2）＝0，建方程）③可用正交矩阵相似对角化.（即存在正交矩阵P，使P－1AP＝PTAP＝Λ）见例8.12至例8.15.（2）若A为正交矩阵，则ATA＝EA－1＝ATA由规范正交基组成AT是正交矩阵A－1是正交矩阵A*是正交矩阵－A是正交矩阵.（3）若A，B为同阶正交矩阵......
2023-11-21
- 详细阅读
-
行列式计算：高等代数-高等代数详细阅读
，xn）.解此递推关系可以得到例9.15 计算n阶行列式.解：将这个行列式的每一列都拆为两列，进而把行列式分成2n个行列式之和.当n>2时，它们中的每一个都有两列成比例.因此，行列式等于零.当n=1时，行列式等于a1+b1.当n=2时，行列式等于.例9.16 设四阶方阵，计算行列式|A|.解：由于所以|A|2=|A||AT|=|AAT|=4.再因为|A|中a4的系数为正，所以，|A|=2.例9.17 计算n阶循环行列式.解：这里我们记，以ζk=ζk，k=1，2，…......
2023-11-22
-
高等代数：矩阵秩原理及应用详细阅读
解：是.由Am×r是列满秩矩阵，则存在行满秩矩阵Pr×m，使得PA=Er.在等式Am×rBr×n=Om×n两端左边乘P，则有Pr×m=Pr×mOm×n=Or×n及Br×n=ErBr×n=Br×n，比较两式可知B=O.是.显然有A（B-C）=O，利用的结论即得B-C=O.习题3.6.1. 如果AB，BA都是有意义的，那么它们是否具有相等的秩？，As都是n阶方阵，证明：并且等号可以取到.3.6.......
2023-11-22
-
高等代数中的分块矩阵及其应用详细阅读
，As都是方阵，那么形如的分块矩阵称为分块对角矩阵，简称分块对角阵，可以简单地记作diag（A1，A2，…，Es）有下面的三种分块初等矩阵：E=diag（E1，…......
2023-11-22
-
高等代数：矩阵初等变换的操作方法详细阅读
，Ps，使得对所得矩阵再进行列的初等变换，变为即存在一些初等方阵Q1，Q2，…P2P1E=A-1.由于在矩阵的左边乘上一个初等方阵P，相当于对这个矩阵作一个与P相对应的初等行变换.上面两个等式表明，对A依次作P1，P2，…......
2023-11-22
-
高等代数：对称多项式及其应用详细阅读
，xn的对称多项式称为n元初等对称多项式.通常，这n个初等对称多项式依次记作σ1，σ2，…，σn.初等对称多项式是最基本的对称多项式.在一元多项式根与系数的关系中，就会自然地出现初等对称多项式.以x1，x2，…，xn的初等对称多项式.证明：存在性.设对称多项式f（x1，x2，…......
2023-11-22
相关推荐