，λs是线性变换σ的s个不同的特征值，Ti是属于特征值λi的线性无关的特征向量组成的向量组，则向量组T1∪T2∪…，αiri线性无关，1≤i≤s，并且满足条件σ（αij）=λiαij，1≤i≤s，1≤j≤ri.下面来证明向量组是线性无关的.若有一组组合系数kij使得记向量，1≤i≤s，由于这表明，若αi≠0，则αi是属于特征值λi的特征向量，由定理5.7可知向量组α1，α2，…......
2023-11-22
高等代数：计算特征值和特征向量
【摘要】：，αr，并扩充为V的一组基α1，α2，…，n），求αTα的特征值.10.1.5. 证明方阵A可逆的充分必要条件是它的特征值均不是零.10.1.6. 若A可逆，证明：A-1的特征值是A的特征值的倒数.10.1.7. 证明：A2的全部特征值是A的特征值的平方.10.1.8. 证明：若λ1，λ2，…，f（λn）是矩阵f的全部特征值.10.1.9. 求出只与自身相似的所有方阵.10.1.10. 证明：A与AT相似.
第5章中引入了线性变换及其矩阵的特征值与特征向量，以及对角化的概念，并且证明了在n维线性空间中的线性变换σ或其矩阵A可以对角化的充分必要条件是它具有n个线性无关的特征向量.本节，我们利用线性变换的矩阵以及行列式与线性方程组的理论研究线性变换的特征值及特征向量的计算方法.
首先重述一下特征值、特征向量等重要概念.
定义10.1 设V是数域F上的n维线性空间，σ是V上的一个线性变换，若存在数λ∈F以及非零向量α∈V使得
σ（α）=λα，则称λ是σ的一个特征值，非零向量α称为属于特征值λ的特征向量.
定义10.2 设A是数域F上的n阶方阵，若存在数λ∈F以及非零列向量x使得
Ax=λx
则称λ是方阵A的一个特征值，非零向量x称为属于特征值λ的特征向量.
定义10.3 若线性变换σ在某组基之下的矩阵是对角形矩阵，则称这个线性变换σ是可以对角化的；若n阶方阵A与一个对角形矩阵相似，则称这个方阵A是可以对角化的.
由于线性变换及其矩阵之间有明显的对应关系，因此我们只研究矩阵的特征值与特征向量，以及矩阵的对角化问题.
若λ是方阵A的特征值，则由定义10.2知道
Ax=λx， （10.1）
移项整理就得到
（λE-A）x=0. （10.2）
将式（10.2）看作一个线性方程组，那么就得到特征值λ是使得方程组（10.2）有非零解的值.由Cramer法则可以知道这等价于行列式
|λE-A|=0. （10.3）
以上分析表明矩阵A的特征值是使得式（10.3）成立的值，而特征向量是方程组（10.2）的非零解.这里，行列式λE-A是关于变量λ的多项式，称之为矩阵A的特征多项式，记作fA（λ）或f（λ），其根为矩阵A的特征值或特征根.
若λ是方阵A的特征值，则线性方程组（λE-A）x=0的解空间
Vλ={x|Ax=λx}
称为特征值λ的特征子空间.
由于每一个线性变换σ都对应于一个矩阵A，把fA（λ）也称为线性变换σ的特征多项式，这时也记作fσ（λ）.
由方程组的理论可以知道，特征多项式的根都是特征值.特征值作为特征多项式的根的重数称为该特征值的代数重数；而每一个特征值λ的特征子空间Vλ的维数dimVλ称为这个特征值的几何重数.
命题10.1 相似的矩阵有相同的特征多项式.
证明：设矩阵A，B相似，即存在可逆矩阵P，使得A=P-1BP.因此，利用行列式性质可得
|λE-A|=|P-1（λE）P-P-1BP|
=|P-1（λE-B）P|
=|P-1λ||E-B||P|
=|λE-B|，
即A，B的特征多项式相同.
例10.1 若二阶方阵
按照定义有它们的特征多项式相等，
fE（λ）=fA（λ）=（λ-1）2.
但是，很容易看到单位阵只能与自己相似，因此这两个矩阵不相似.也就是说，命题10.1的逆是不成立的.
例10.2 设
，则A的特征多项式为
所以，方阵A的两个特征值为λ1=1，λ2=2.
解线性方程组（λ1E-A）x=0，可得λ1=1的特征向量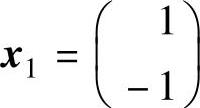
；解线性方程组（λ2E-A）x=0，可得λ2=2的特征向量
.
如果记
则有
所以
例10.3 设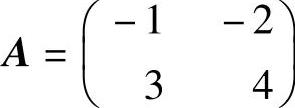
，计算A10和An.(www.chuimin.cn)
解：由例10.2知道，对于矩阵A，如果我们取矩阵
那么就有矩阵P的逆矩阵为
并且有
因此，
即
于是可得
同理，可得对自然数n，有
例10.4 设三阶方阵
A的特征多项式为
进而得到三个特征值λ1=-1，λ2，3=1.
解线性方程组（λ1E-A）x=0，可得λ1=-1的特征向量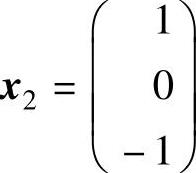
.
解线性方程组（λ2E-A）x=0，可得λ2=1的特征向量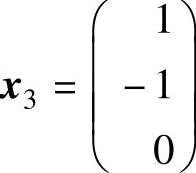
和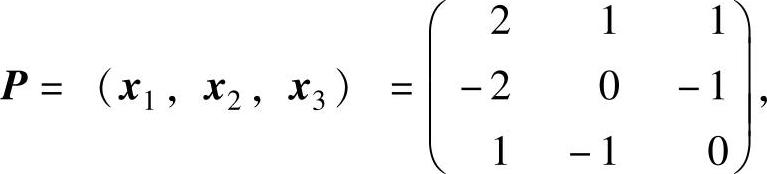
.
取三阶方阵
则有
例10.5 设二阶方阵
A的特征多项式
fA（λ）=|λE-A|=（λ-1）2
的特征值是λ1，2=1.解方程组（λ1E-A）x=0可得属于特征值λ1=1的特征向量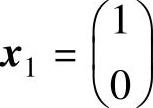
.由于二阶方阵A只有一个线性无关的特征向量，因此，A不能对角化.
在例10.4中，-1的几何重数和代数重数均为1；1的几何重数和代数重数均为2.在例10.5中，1的几何重数是1，而代数重数是2.一般地，一个特征值的几何重数是不会超过其代数重数的.
定理10.1 几何重数≤代数重数.
证明：设线性变换σ（或者方阵A）的特征值λ0的几何重数是r.取Vλ0的一组基α1，α2，…，αr，并扩充为V的一组基α1，α2，…，αn，则σ在这组基之下的矩阵是形如
的矩阵.其特征多项式是
f（λ）=（λ-λ0）r|λE-A2|.
显然，λ0的几何重数≤λ0的代数重数.
线性变换或其矩阵的特征值与特征向量与数域F有密切关系.例如，考虑二阶方阵
通过简单计算可以知道，这个矩阵A的特征多项式为λ2+1，在实数范围内没有解.这也就意味着，矩阵A在实数范围内没有特征值，当然也就没有特征向量.但是，如果我们把这个矩阵放在复数范围内考虑的话，就很容易看到A有两个不等的特征值±i，并且也容易求得它们各自的一个特征向量
由此可以看到，矩阵A在复数域内是可以对角化的，但是在实数域内则否.
习题
10.1.1. 判断下列方阵是否可以对角化.
10.1.2. 求出下列方阵的相似标准形.
10.1.3. 计算An，其中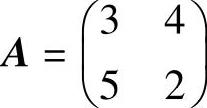
.
10.1.4. 设α=（1，2，…，n），求αTα的特征值.
10.1.5. 证明方阵A可逆的充分必要条件是它的特征值均不是零.
10.1.6. 若A可逆，证明：A-1的特征值是A的特征值的倒数.
10.1.7. 证明：A2的全部特征值是A的特征值的平方（注意重数）.
10.1.8. 证明：若λ1，λ2，…，λn是n阶方阵A的全部特征值，且互不相同，而f（x）是一个多项式，则有f（λ1），f（λ2），…，f（λn）是矩阵f（A）的全部特征值.
10.1.9. 求出只与自身相似的所有方阵.
10.1.10. 证明：A与AT相似.
有关高等代数的文章
- 详细阅读
-
行列式计算：高等代数-高等代数详细阅读
，xn）.解此递推关系可以得到例9.15 计算n阶行列式.解：将这个行列式的每一列都拆为两列，进而把行列式分成2n个行列式之和.当n>2时，它们中的每一个都有两列成比例.因此，行列式等于零.当n=1时，行列式等于a1+b1.当n=2时，行列式等于.例9.16 设四阶方阵，计算行列式|A|.解：由于所以|A|2=|A||AT|=|AAT|=4.再因为|A|中a4的系数为正，所以，|A|=2.例9.17 计算n阶循环行列式.解：这里我们记，以ζk=ζk，k=1，2，…......
2023-11-22
- 详细阅读
-
高等代数中集合与其运算-高等代数详细阅读
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2023-11-22
-
矩阵特征值与特征向量详细阅读
，1）T.由于方程组的系数矩阵的n-1阶子式所以，方程组的系数矩阵的秩为n-1，从而α0是方程组的一个基础解系.因此λ=a+（n-1）b对应的所有特征向量为.设对应特征值λ=a-b的特征向量为y=（y1，y2，…......
2023-10-27
-
高等代数-直和定理：Rn=W1⊕W2详细阅读
+Ws是直和，记作W1⊕W2⊕…⊕Ws.定理4.11 设W1，W2，…+dimWs..分别取每个子空间Wi的一组基αij，1≤j≤ri，其中dimWi=ri.由条件可以知道向量组αij，1≤i≤s，1≤j≤ri是和空间W的一组基，因此一定线性无关，由直和的定义知道W=W1+W2+…=xn}，证明：Rn=W1⊕W2.4.7.3. 在线性空间Rn中，取向量α1，α2，…......
2023-11-22
-
特征值与特征向量的定义详细阅读
设A是n 阶矩阵，λ是一个数，若存在n维非零列向量ξ，使得则称λ是A 的特征值，ξ是A 的对应于特征值λ的特征向量.由①式，得ξ＝0，因ξ≠0，故齐次方程组x＝0有非零解，于是②式称为A 的特征方程，是未知量λ的n次方程，有n个根，λE－A称为特征矩阵，|λE－A|称为特征多项式.求出λi（i＝1，2，…......
2023-11-21
-
高等代数：线性空间的定义详细阅读
定义4.1 设F是数域，V是一个非空集合，V中的元素具有两种运算，分别称为加法运算和数乘运算.所谓加法运算，就是一个对应法则，该法则使得集合V中任意两个元素α，β都对应于集合V中一个确定的元素γ，并称γ为元素α与β的和，记作γ=α+β.数乘运算是集合V中元素与数域F中的元素之间的运算法则，该法则使得集合V中任意一个元素α与数域F中任意一个数k，都对应于V中一个确定的元素δ，并称δ为k与α的数量乘积......
2023-11-22
相关推荐