【摘要】:,n的一个排列,eγ是第γ分量为1,其余分量为0的n维列向量.再把行列式按前n-s列展开得由于=n2+s2-ns+2n-s,所以有又由于-=n(n+1)+s(s-1)-2ns是一个偶数,所以,n2+s2-ns+2n-s和ns+n有相同的奇偶性.从而得到定理9.19 设A,B分别是s×n,n×t阶矩阵,C=AB,r是一个正整数,则当r>n时,;当r≤n时,证明:利用矩阵乘法规则可以看到,从矩阵A中选出第i1,i2,…
1.Cramer法则
这里将要讨论的是线性方程组的公式解.首先设n元一次线性方程组
通常把这个方程组的系数矩阵的行列式记作D,称为系数行列式,即
并且记
其中1≤j≤n.这里Dxj是把系数行列式中的第j列的全部元素用常数项依次换掉之后得到的行列式.我们有如下定理.
定理9.12 (Cramer法则)n元一次线性方程组(9.16)有唯一解的充分必要条件是其系数行列式D≠0;并且在此时,线性方程组(9.16)的解为
证明:只需验证后一半结论即可.利用行列式展开定理,有
这里1≤i≤n.证毕.
推论9.9 齐次线性方程组
有非零解的充分必要条件是D=0.
2.伴随矩阵
设A=(aij)是n阶方阵,称由这个方阵的全部代数余子式构成的n阶方阵
为方阵A的伴随矩阵,记作A∗.由行列式展开定理,容易证明:
定理9.13 对任意的n阶方阵A都有AA∗=A∗A=|A|E.
这样,我们可以得到一个计算逆矩阵的公式.
定理9.14 当方阵A可逆时,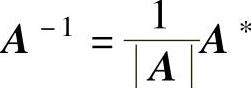 .
.
3.矩阵的秩
若A是m×n阶矩阵,任意选择k行以及k列,交叉位置的元素依其原有的相对位置组成的行列式称为A的一个k阶子式.
定理9.15 若A是m×n阶矩阵,则rankA=r的充分必要条件是A有一个r阶子式不等于零,而所有r+1阶子式全等于零.
证明:充分性,有一个r阶子式不等于零,说明A有r个线性无关的列向量,即rankA≥r;所有r+1阶子式全等于零,说明A的任意r+1个列向量都是线性相关的,即rankA≤r.于是有rankA=r.
必要性,先选择r个线性无关的列,再从中选择r个线性无关的行,则由这些元素组成的子式就不等于零.而r+1个列向量一定线性相关,任意选r+1个行,则得到的子式一定是零.证毕.
这个定理使得我们可以有另外一种定义秩的方法.
定义9.4 矩阵中不为零的子式的最高阶数称为该矩阵的秩.
至此,我们有三种定义矩阵的秩的方法,它们是:
(1)相抵标准形中1的个数,或者非零行的行数,或者非零列的列数;
(2)行秩或者列秩;
(3)非零子式的最高阶数.
4.正定矩阵
引理9.3 正定矩阵的行列式大于零.
证明:若A是正定矩阵,则存在可逆矩阵P,使得A=PTP,所以|A|=|PTP|=|P|2>0.证毕.
设A是对称方阵,选择下标列1≤i1<i2<…<ik≤n,则子式
称为A的主子式,而子式
称为A的顺序主子式.
定理9.16 (Hurwitz)设A是对称方阵,则A正定的充分必要条件是A的顺序主子式全大于零.
证明:必要性.设A是正定矩阵,其二次型为
考虑主子式
其矩阵为
A1的二次型是
若(x1,x2,…,xk)≠0,则有
g(x1,x2,…,xk)=f(x1,x2,…,xk,0,…,0)>0,
因此,g(x1,x2,…,xk)是正定二次型,由引理知A1>0.必要性得证.
充分性.对n用归纳法.当n=1时,命题显然成立.假设命题对n-1阶方阵成立,对于n阶方阵A,把方阵A分块为
这时,An-1是对称方阵,且顺序主子式全都大于零,因此An-1是正定矩阵.所以,有矩阵恒等式
由条件可知
ann-αTA-1n-1α>0.
进一步可得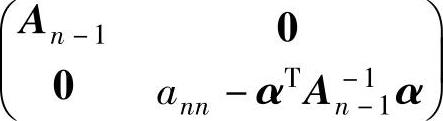 与En合同.因此A是正定矩阵.证毕.
与En合同.因此A是正定矩阵.证毕.
定理9.17 设A是对称方阵,则A正定的充分必要条件是A的主子式全大于零.
证明留作习题.
5.Binet-Cauchy公式
矩阵A中第i1,i2,…,ik行和第j1,j2,…,jk列的交叉元素按照原来的相对位置组成的k阶子式,记作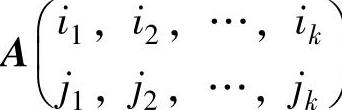 .
.
定理9.18 (Binet-Cauchy公式)设A,B分别是s×n,n×s阶矩阵,则有
(1)当s>n时,AB=0;
(2)当s=n时,AB=AB;
(3)当s<n时, .
.
证明:(1)此时,rankAB≤n<s,所以AB=0.
(2)前面已证明的结论.
(3)考虑分块矩阵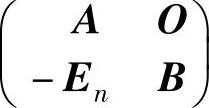 ,易于验证
,易于验证
这样,利用(2)的结论知,上式左端的行列式就等于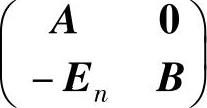 的行列式,因此,有(www.chuimin.cn)
的行列式,因此,有(www.chuimin.cn)
把右端的行列式按前n列展开得
把左端的行列式按前s行展开得
其中,j1<j2<…<jn-s,i1i2…is,j1j2…jn-s是1,2,…,n的一个排列,eγ是第γ分量为1,其余分量为0的n维列向量.
再把行列式 按前n-s列展开得
按前n-s列展开得
由于
=n2+s2-ns+2n-s,
所以有
又由于
(n2+s2-ns+2n-s)-(ns+n)=n(n+1)+s(s-1)-2ns
是一个偶数,所以,n2+s2-ns+2n-s和ns+n有相同的奇偶性.从而得到
定理9.19 设A,B分别是s×n,n×t阶矩阵,C=AB,r是一个正整数,则
(1)当r>n时, ;
;
(2)当r≤n时,
证明:利用矩阵乘法规则可以看到,从矩阵A中选出第i1,i2,…,ir行构成矩阵A1,从矩阵B中选出第j1,j2,…,jr列构成矩阵B1,那么
引用Cauchy-Binet公式即可.证毕.
例9.18 设
其中ai,bi,1≤i≤n,都是实数,下面计算行列式|AAT|.
首先,利用Binet-Cauchy公式有
其次,通过直接计算可得
因此,有Lagrange恒等式
再注意到等式的右端非负,因此可得Cauchy-Schwarz不等式:
习题
9.7.1. 利用Cramer法则解下列线性方程组.
9.7.2. 解线性方程组
并讨论其解的情况,x,y,z是变量.
9.7.3. 已知方程组
有唯一解,证明:abc≠0,并求解.
9.7.4. 设n阶方阵A的伴随矩阵是A∗.
(1)证明:|A∗|=|A|n-1.
(2)计算:rankA∗.
(3)计算:(A∗)∗.
9.7.5. 证明:n阶方阵
是正定矩阵.
9.7.6. 设A,B分别是m×n,n×s阶矩阵,证明:对m×s阶矩阵C=AB的任意一个r阶子式 都有
都有
(1)当r>n时, ;
;
(2)当r≤n时,
9.7.7. 设A,B都是n阶方阵,
(1)证明:AB和BA的m阶主子式之和相等;
(2)证明:|λE-AB|=|λE-BA|.
9.7.8. 设A,B分别是m×n,n×m阶矩阵,证明:
λn|λE-AB|=λm|λE-BA|.
9.7.9. 利用Binet-Cauchy公式证明AAT的任意主子式都是非负的.
9.7.10. 证明下列恒等式.
(1)Euler恒等式
(x21+x22+x23+x24)(y21+y22+y23+y24)
=(x1y1+x2y2+x3y3+x4y4)2+
(x1y2-x2y1-x3y4+x4y3)2+
(x1y3+x2y4-x3y1-x4y2)2+
(x1y4-x2y3+x3y2-x4y1)2;
(2)Cauchy恒等式
(3)
(a3+b3+c3-3abc)(x3+y3+z3-3xyz)
=A3+B3+C3-3ABC,
其中A=ax+by+cz,B=az+by+cx,C=ay+bx+cz.
9.7.11. (1)计算三阶行列式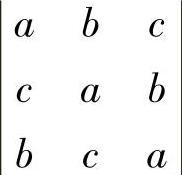 .
.
(2)将三元三次多项式a3+b3+c3-3abc分解因式.

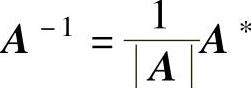
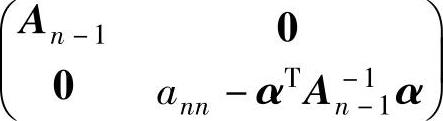 与
与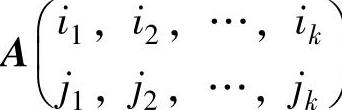

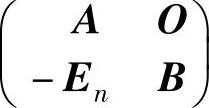 ,易于验证
,易于验证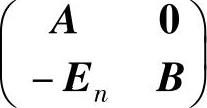 的行列式,因此,有(www.chuimin.cn)
的行列式,因此,有(www.chuimin.cn) 按前
按前 ;
; 都有
都有 ;
;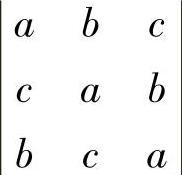







相关推荐