首页 理论教育行列式的展开和Laplace定理简介

行列式的展开和Laplace定理简介

2023-11-22 理论教育 版权反馈
【摘要】：，n}.Laplace定理就是说行列式D等于下面我们只对ik=k，1≤k≤r，的情形给出证明，这一情形就是按照前r行展开，其他情形都可以化为这种情形后予以证明.此时，Laplace定理就是行列式D等于首先，按照行列式的定义，行列式D的展开式是n！项代数式的代数和；而式完全展开成aij乘积之后的项数是r！.因此，行列式D的展开式与式所含项数相等.不考虑符号的话，D的展开式的一般项为，其中j1，j2，…

在n阶行列式

中，去掉元素aij所在的第i行第j列的所有元素，其余的元素按原来的相对位置排列，形成的n-1阶行列式

称为元素aij的余子式，记作Mij，并称Aij=（-1）i+jMij为元素aij的代数余子式.

代数余子式与行列式有密切的联系，行列式可以用它的元素与代数余子式共同表示出来.在得到这个结果之前，先来证明一个有用的引理.

引理9.1 若n阶方阵

那么有

证明：由于a1j=0，j=2，3，…，n，τ（1j2…jn）=τ（j2…jn），所以

证毕.

引理9.2 若方阵A的第i行除元素aij外，其余元素均为零，则A的行列式|A|=aijAij.

证明：将|A|的第i行依次与上面的i-1行互换，将第j列依次与左边的j-1列互换，再用引理9.1得

证毕.

至此，我们可以证明行列式的按行或列的展开定理.

定理9.9（行列式展开定理） 设n阶行列式D=|aij|，则有

D=ai1Ai1+ai2Ai2+…+ainAin，

D=a1jA1j+a2jA2j+…+anjAnj，

其中Aij是元素aij的代数余子式，i，j=1，2，…，n.

证明：将行列式D的第i行的每一个元素加上n-1个零，再由定理9.4及引理9.2可得

同理可证第二个等式.证毕.

引入Kronecker符号，其定义为

利用这个符号有：

推论9.8 设n阶行列式D=|aij|，则

ai1Aj1+ai2Aj2+…+ainAjn=Dδij， （9.9）

a1iA1j+a2iA2j+…+aniAnj=Dδij， （9.10）

这里，δij是Kronecker符号，1≤i，j≤n.

证明：只证明式（9.9）.这是简单的，只需要注意到根据定理9.9，式（9.9）左边应该表示将行列式D=|aij|的第j行元素用第i行元素全部对应替换掉之后得到的行列式D′.由定理9.9及推论9.4可以知道当i=j时，行列式D′=D；当i≠j时，行列式D′=0.证毕.

例9.6 计算三阶行列式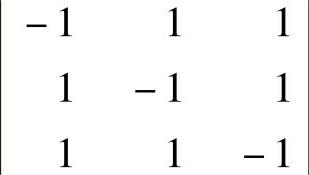978-7-111-50689-8-Chapter09-52.jpg.

解：把行列式按第一行展开，得到

在n阶行列式D中，任取k行i1，i2，…，ik，再任取k列j1，j2，…，jk，行列交叉处的元素按原来的相对位置排成的k阶行列式M，称为行列式D的一个k阶子式，记作

在行列式D中去掉上面选择k行与k列，剩下的元素按原来的相对位置排成的n-k阶行列式M′，称为M的余子式.在M′前加上符号

后所得到的代数式，称为子式M的代数余子式.

定理9.10（Laplace定理） 在n阶行列式中任取k行（或者列），1≤k≤n，则由这k行（或者列）元素组成的所有k阶子式与其各自的代数余子式的乘积的和等于行列式的值.

证明：设n阶行列式D=|aij|n×n，两组自然数指标

1≤i1<i2<…<ir≤n，1≤i′1<i′2<…<i′n-r≤n，

满足条件

{i1，i2，…，ir}∪{i′1，i′2，…，i′n-r}={1，2，…，n}.

Laplace定理就是说行列式D等于

下面我们只对ik=k，1≤k≤r，的情形给出证明，这一情形就是按照前r行展开，其他情形都可以化为这种情形后予以证明.此时，Laplace定理就是行列式D等于

首先，按照行列式的定义，行列式D的展开式是n！项代数式的代数和；而式（9.11）完全展开成aij乘积之后的项数是r！（n-r）！（nr）=n！.因此，行列式D的展开式与式（9.11）所含项数相等.

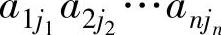不考虑符号的话，D的展开式的一般项为978-7-111-50689-8-Chapter09-58.jpg，其中j1，j2，…，jn要取遍1，2，…，n的所有全排列.容易看到，这样的项一定出现在式（9.11）中.因此欲证结论，只需证明在D的展开式与式（9.11）中一般项978-7-111-50689-8-Chapter09-59.jpg的符号也相等即可.

先考虑简单的情况，即考虑在一般项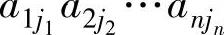978-7-111-50689-8-Chapter09-60.jpg中，j1，j2，…，jr是1，2，…，r的一个排列的情况.此时，在D的展开式中该项的符号是

在式（9.11）中的该项的符号是

注意到，j1j2…jr是1，2，…，r的一个排列，因此，

τ（j1j2…jn）=τ（j1j2…jr）+τ（jr+1jr+2…jn）.

显然，有(www.chuimin.cn)

这就是说，在这种情形下一般项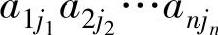978-7-111-50689-8-Chapter09-64.jpg在两个表达式的符号相等.

对于一般的情况，也就是考虑一般项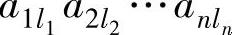978-7-111-50689-8-Chapter09-65.jpg，此项出现在式（9.11）的乘积

中，这里，j1j2…jr是l1，l2，…，lr由小到大的排列，j′1j′2…j′n-r是lr+1，lr+2，…，ln的由小到大的排列.

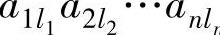978-7-111-50689-8-Chapter09-67.jpg在D的展开式中的符号是

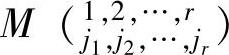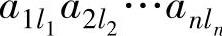为了考虑在式（9.8）中的符号，把子式978-7-111-50689-8-Chapter09-69.jpg移到右上角的位置.移动方法如下：把第j1列依次与前一列作对换，直到移至第一列，在这一过程中，项978-7-111-50689-8-Chapter09-70.jpg978-7-111-50689-8-Chapter09-71.jpg的符号改变了j1-1次；再把第j2列依次与前一列作对换，直到移至第二列，在这一过程中，项978-7-111-50689-8-Chapter09-72.jpg的符号改变了j2-2次；以此类推，直到把第jr列移至第r列为止.计算可以知道，在这一过程中，项978-7-111-50689-8-Chapter09-73.jpg的符号改变了（j1-1）+（j2-2）+…+（jr-r）次.

由前面已经证得的结论可以看到，项978-7-111-50689-8-Chapter09-74.jpg在D中的符号经过

（j1-1）+（j2-2）+…+（jr-r）

次改变，与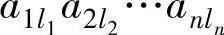978-7-111-50689-8-Chapter09-75.jpg在

中的符号相等.再注意到，改变

（j1-1）+（j2-2）+…+（jr-r）

次符号，与改变

（j1+1）+（j2+2）+…+（jr+r）

次符号是一样的.因此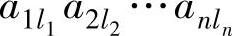，978-7-111-50689-8-Chapter09-77.jpg的符号在D的展开式与式（9.11）中是一样的.证毕.

例9.7 计算六阶行列式978-7-111-50689-8-Chapter09-78.jpg

解：利用Laplace定理，按一、三、五列展开，在一、三、五列中，二、四、六行的元素全是零，因此在展开式中非零项只有一项，由此得到

定理9.11 设A，B均为n阶矩阵，则|AB|=|A||B|.

证明：如果rankA<n或rankB<n，那么rankAB<n，因此|AB|=0=|A||B|.

如果rankA=rankB=n，这时可以分成四种情况逐一讨论.

（1）B=E（i，j）时，由定理9.6，|AB|=-|A|，|B|=-1，从而|AB|=|A||B|.

（2）B=E（i（k））时，由定理9.5，|AB|=k|A|，|B|=k，从而|AB|=|A||B|.

（3）B=E（i，j（k））时，由定理9.7，|AB|=|A|，|B|=1，从而|AB|=|A||B|.

（4）B为任意可逆矩阵，则B=P1P2…Pt，其中Pi为初等矩阵，由（1），（2），（3）可得

|AB|=|AP1P2…Pt-1Pt|

=|AP1P2…Pt-1||Pt|

=…

=|A||P1||P2|…|Pt|.

同理可得

|B|=|EP1…Pt|

=|E||P1|…|Pt|

=|P1|…|Pt|.

从而|AB|=|A||B|.

证毕.

例9.8 设O是正交矩阵，证明：O的行列式只能是±1.

证明：由于OTO=E，因此|OTO|=|E|=1，于是

1=|OTO|=|OT||O|=|O|2，

即|O|=±1.

例9.9 证明：对称矩阵的行列式等于它的全部特征值的乘积.

证明：设n阶对称矩阵的全部特征值是λ1，λ2，…，λn，则存在正交矩阵O，使得

OTAO=diag（λ1，λ2，…，λn）.

两边取行列式，再利用例9.8的结论可得|A|=λ1λ2…λn.

习题

9.5.1. 利用Laplace定理计算行列式.

9.5.2. 证明恒等式：（ab′-a′b）（cd′-c′d）-（ac′-a′c）（bd′-b′d）+（ad′-a′d）（bc′-b′c）=0.

有关高等代数的文章

  • 行列式初步及克莱姆法则定理1简介 行列式初步及克莱姆法则定理1简介

    ，xn和n个方程的线性方程组为定理1 克莱姆法则 如果方程组（3.2）的系数行列式则方程组（3.2）有唯一解即Dj是把系数行列式D的第j列元素a1j，a2j，…，anj换为方程组右端常数项b1，b2，…，Anj分别乘以（3.4）的第1、第2、…、第n个等式，再把n个等式两边相加得根据n阶行列式的定义，上式即为因为D≠0，所以cj=Dj/D（j=1，2，…，n），则方程组称为n元齐次线方程组.n元齐次线性方程组显然必有零解（即xj=0，j=1，2，…......

    2023-11-20

    详细阅读
  • n阶行列式展开规则及解析 n阶行列式展开规则及解析

    设n阶行列式则有Dn=ai1Ai1+ai2Ai2+…+anjAnj（Dn按第j列展开，j=1，2，…，n），其中，Aij是元素aij的代数余子式，即（-1）i+j与Dn中去掉第i行和第j列元素后的n-1阶行列式之积.注ak1Ai1+ak2Ai2+…，n，但k≠i），a1kA1j+a2kA2j+…......

    2023-10-27

    详细阅读
  • 洛朗级数展开定理、复变函数及应用 洛朗级数展开定理、复变函数及应用

    在圆环域R1 ＜|z-z0|＜R2内处处解析的函数f(z)可以展开成z-z0的正、负幂项都有的级数,称为f(z)的洛朗(Laurent) 级数.定理1(洛朗级数展开定理) 设R1 ＜|z - z0| ＜R2 为环域D,函数f(z)在D内解析,则对D 内任意点z有其中C为在该环域内任意一条围绕点z0的正向简单闭路.证明对任意z ∈D,在D内分别作正向圆周C1 和C2,其中C1为|ζ-z0|=r1,C......

    2023-10-30

    详细阅读
  • 圆周角定理及推论简介 圆周角定理及推论简介

    顶点在________，两边都与圆相交，这样的角叫做圆周角；圆周角定理：一条弧所对的圆周角等于它所对的圆心角的________；推论：在同圆或等圆中，同弧或等弧所对的圆周角_________．1．如图，AB，BC都是⊙O的弦，∠ABC＝40°，则∠AOC＝（ ）．A．50° B．60° C．80° D．90°（第1题）2．如图，BC是⊙O的弦，OA⊥BC，∠AOB＝55°，则∠ADC＝（ ）．（第......

    2023-07-03

    详细阅读
  • 从数学教育到教育数学，逻辑展开与平行线定理 从数学教育到教育数学，逻辑展开与平行线定理

    命题5.4.1设M、N两点在直线AB的同侧，则MN∥AB的充分必要条件是△MAB＝△MAB。这是上一小节已证明的例题5.3.9。命题5.4.2两直线AB、CD和另一直线l交于P、Q，若同位角相等，则AB∥CD。于是，共角比例定理可以完善成为命题5.4.4若△ABC与△A′B′C′中，有∠A＝∠A′或∠A+∠A′＝180°，则。命题5.4.5PQ∥AB，若直线l与AB垂直，则l也和PQ垂直。推论5.4.2平行线处处等距。推论5.4.3若直线l1∥l2，而l3与l1、l2相截，则内错角相等。......

    2023-10-17

    详细阅读
  • 罗尔定理的证明和费马定理的基本性质 罗尔定理的证明和费马定理的基本性质

    从几何上可以看到：在对于两端高度相等的连续光滑曲线上，必存在一条水平的切线（如图3－1所示），这便是罗尔定理.为了罗尔定理证明的需要，下面先给出极值的定义和极值点的一条基本性质——费马定理.图3－1定义1设f（x）在点x0的某邻域内有定义，若x∈（x0，δ），恒有f（x）＜f（x0）（或f（x）＞f（x0）），则称f（x0）为f（x）的一个极大值（或极小值），函数的极大值与极小值统称为函数的极值......

    2023-11-19

    详细阅读
  • 不动点定理及相关概念简介 不动点定理及相关概念简介

    ,fk是关于变元x1,x2,…,xn的一组n 元多项式.方程组f1=f2=…=fk=0 无公共零点的充要条件是:存在另一组n 元多项式a1,a2,…,ak,使得a1f1＋a2f2＋…......

    2023-10-20

    详细阅读
  • 拉格朗日中值定理和柯西中值定理的应用 拉格朗日中值定理和柯西中值定理的应用

    【主要内容】1.拉格朗日中值定理设函数f（x）在闭区间[a，b]上连续，在开区间（a，b）内可导，则存在ξ∈（a，b），使得f（b）-f（a）=f′（ξ）（b-a）.2.柯西中值定理设函数f（x）和g（x）都在闭区间[a，b]上连续，在开区间（a，b）内可导，且g′（x）≠0（x∈（a，b）），则存在ξ∈（a，b），使得当函数f（x）在[a，b]上连续，在（a，b）内可导，但不易确定f（a）=f（......

    2023-10-27

    详细阅读