的自然数）阶完美或对称完美的砍尾巴幻方？细心的读者应已意识到，如果第一步中我们构造的B是一个完美幻方，同时解除第二步中关于数列是中心对称的限制，我们得到的就是一个完美的掐头去尾幻方.......
2023-10-20
行列式的性质及奇数阶反对称方阵
【摘要】：本节的目的是研究行列式的基本性质，为计算行列式的值提供有力的工具.为书写简便起见，我们借助矩阵的一些记号.设n阶矩阵A的列向量组为α1，α2，…+an，证明恒等式9.4.7. 证明：奇数阶反对称方阵的行列式一定是零.
本节的目的是研究行列式的基本性质，为计算行列式的值提供有力的工具.为书写简便起见，我们借助矩阵的一些记号.设n阶矩阵A的列向量组为α1，α2，…，αn，这时也可以记
|A|=|α1，α2，…，αn|.
设A为n阶方阵，通常把行列式|AT|称为行列式|A|的转置行列式，并且我们有下面定理.
定理9.3 行列式与它的转置行列式相等，即
证明：引入一组新的符号b.，把aij记作bji.那么式（9.4）的右边就可以记作
利用行列式的定义分别计算式（9.4）的两端得到
由定理9.2可以知道，左边=右边.证毕.
定理9.3表明行列式的行与列具有对称性，即是说，对于列成立的性质，关于行也同样成立.为叙述简单起见，以下我们只对列证明行列式的性质.
定理9.4 若两个n阶行列式有n-1个对应列（或者行）完全相同，那么它们的和等于那个不同列（或者行）上的对应元素相加，其他列（或者行）都不变的行列式的值，即
或者记为
|α1，…，α2，…，αn|+|α1，…，α′i，…，αn|=|α1，…，αi+α′i，…，αn|.
证明：利用行列式的定义，可以得到式（9.5）的
证毕.
定理9.5 若行列式的某一列（或者行）全部元素有一个公共的因子，那么这个因子可以提到行列式外面，即
或者记为
|α1，…，kαi，…，αn|=k|α1，…，αi，…，αn|.
证明：利用行列式的定义，可以得到式（9.6）的
证毕.
定理9.4与定理9.5表明行列式对于列（或者行）具有线性性质.
推论9.2A是n阶方阵，k为常数，则|kA|=kn|A|.
证明：只需要注意到行列式|A|的每一列都可以提出一个因子k即可.证毕.
推论9.3 若行列式的某一列（或者行）的全部元素都是零，那么这个行列式必为零.
证明：只需要提出因子零即可.证毕.
定理9.6 交换行列式的任意两列（或者行）行列式变号，即
或者记为
|…，αi，…，αj，…|=-|…，αj，…，αi，…|.
证明：设(www.chuimin.cn)
A=（aij）=（α1，…，αk，…，αl，…，αn），
B=（bij）=（α1，…，αl，…，αk，…，αn），
即当j≠k，l时，bij=aij，bil=aik，bik=ail.由行列式的定义及定理9.2有
证毕.
推论9.4 若行列式中有两列（或者行）完全相同，那么这个行列式的值为零.
证明：交换这相同的两列行列式显然没有改变，但是，定理9.6又断言它应该变号，故此这个值只能是零.证毕.
推论9.5 若行列式中有两列（或者行）成比例，那么这个行列式的值为零.
证明：将比例系数提出行列式，再利用推论9.4.证毕.
定理9.7 把行列式的某一列（或者行）的全部元素乘以同一个数加到另外一列（或者行）的对应元素上去，行列式的值不变，即
或者写成
|…，αi，…，αj+kαi，…|=|…，αi，…，αj，…|.
证明：由定理9.4与推论9.5易得
证毕.
推论9.6 若方阵A的列向量组（或者行向量组）线性相关，则|A|=0.
推论9.7 若方阵A的列向量组（或者行向量组）线性无关，则|A|≠0.
证明：由于A的列向量组线性无关，A为可逆矩阵，从而A与单位矩阵相抵.注意：互换矩阵的两列（行），其行列式仅改变符号；某一列（行）乘非零常数倍，等于行列式乘相应的倍数；把某一列（行）的若干倍加到另外一列（行）上，行列式的值不变.由于|E|=1≠0，所以|A|≠0.证毕.
把上面的推论结合在一起可以得到矩阵可逆的又一个充分必要条件.
定理9.8 方阵A可逆的充分必要条件是|A|≠0.
习题
9.4.1. 不用计算，证明行列式
一定是3的整数倍.
9.4.2. 利用行列式的性质计算下列行列式的值.
9.4.3. 证明：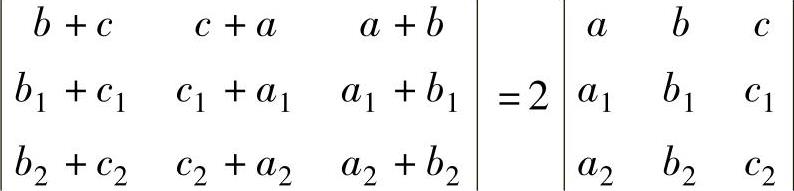
.
9.4.4. 证明恒等式：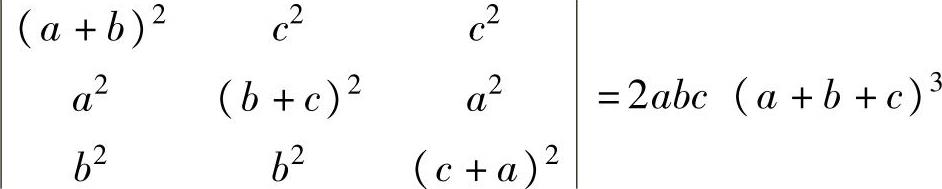
.
9.4.5. 证明恒等式：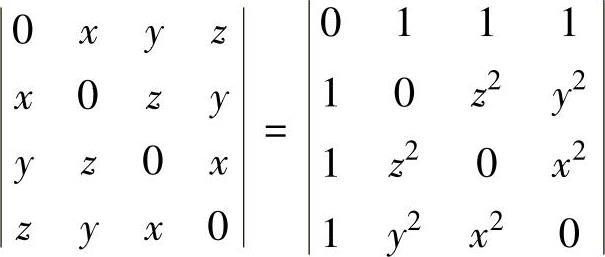
.
9.4.6. 若s=a1+a2+…+an，证明恒等式
9.4.7. 证明：奇数阶反对称方阵的行列式一定是零.
有关高等代数的文章
- 详细阅读
-
完美幻立方的奇数阶空间对称截面详细阅读
，7的自然数）阶空间对称截面完美幻立方的三步法[9]：第一步，按文[1]构造奇数n=2m+1（m＝1，2，…，n）个位置得截面方阵Ck.按k由小到大的顺序，此k个截面组成的数字立方阵C就是一个奇数n=2m+1（m为m≠3t+1且m≠5s+2t，s＝0，1，2，…的自然数）阶空间对称截面完美的幻立方.......
2023-10-20
-
n阶行列式的概念及性质初步解析详细阅读
，n）排成n行n列且其值为这里，j1j2…，n的所有不同排列j1j2…jn求和的记号称为n阶行列式，记为Dn或D.2.n阶行列式的性质设D是n阶行列式，则D与它的转置行列式DT（即将D的第i列作为第i行（i=1，2，…......
2023-10-27
-
奇数阶空间对称完美幻立方：幻中之幻详细阅读
的自然数）阶空间对称完美幻立方的三步法[10]：第一步，按文[1]构造奇数n=2m+1（m为m≠3t+1t＝0，1，2，…的自然数）阶对称完美幻方方法的第一步，构造n×n基方阵A.基方阵A位于第i行，第j列的元素为a（i，j）（i，j=1，2，…，n-1第三步，与构造空间完美幻立方步骤的第三步相同，即第k个截面的基方阵Bk第i行的元素按余函数r的规则右移r（i=1，2，…的自然数）阶空间对称完美幻立方.......
2023-10-20
-
n阶行列式展开规则及解析详细阅读
设n阶行列式则有Dn=ai1Ai1+ai2Ai2+…+anjAnj（Dn按第j列展开，j=1，2，…，n），其中，Aij是元素aij的代数余子式，即（-1）i+j与Dn中去掉第i行和第j列元素后的n-1阶行列式之积.注ak1Ai1+ak2Ai2+…，n，但k≠i），a1kA1j+a2kA2j+…......
2023-10-27
-
构造奇数n=2m+1阶空间对称幻立方的三步法详细阅读
第一步，按文[1]构造奇数n=2m+1（m=1，2，…，n.第二步，构造以k轴为法线方向的第k（k=1，2，…，n）个位置得第k个截面的方阵Ck，按k由小到大的顺序，此k个截面Ck，组成的数字立方阵C就是一个奇数n=2m+1（m=1，2，…））2个不同的n阶基方阵，由这些不同的n阶基方阵出发就可分别得出同样数目的不同的奇数n=2m+1（m=1，2，…为自然数）阶空间对称幻立方.......
2023-10-20
- 详细阅读
-
构造5阶对称完美幻方详细阅读
第一步，由构造对称完美幻方的两步法[]1得到的一个5阶对称完美幻方，其幻方常数是65.中心对称位置上两个元素之和都等于26.其基方阵A如图5-1所示，对称完美幻方如图5-2所示.图5-15阶基方阵A图5-25阶对称完美幻方上述5阶对称完美幻方其所有数都加10，得一个新的由11～35的自然数组成的非正规的5阶对称完美幻方B，如图5-3所示.图5-3非正规的5阶对称完美幻方B第二步，从1～9的自......
2023-10-20
相关推荐