，an，b是复数，则形如的方程称之为n元线性方程.由若干个n元线性方程组成的一组方程，称为线性方程组.能够使得线性方程组中所有方程同时成为等式的一组数值，称为方程组的一组解.下面我们初步探讨线性方程组的求解方法.例3.1若公鸡五文钱一只，母鸡三文钱一只，小鸡一文钱三只，现在用一百文钱买到一百只鸡，问：公鸡、母鸡、小鸡各买多少只？......
2025-09-30
高等代数-线性方程组解的条件及证明
【摘要】：，βn，则方程组又可写为的形式.从而有如下定理：定理8.7 线性方程组有解的充分必要条件是b是列向量组β1，β2，…，ηs是对应的齐次线性方程组的一个基础解系.证明：η，η1，η2，…+ksηs也是它的解.8.4.4. 设非齐次线性方程组Ax=b的系数矩阵的秩为r，η1，η2，…
形如
的方程组称为n元线性方程组.其中矩阵
称为这个线性方程组的系数矩阵，而增加常数项一列之后的矩阵
称为这个线性方程组的增广矩阵，
称为常数项，则方程组（8.16）可以简记为Ax=b.
将A的列向量依次记为β1，β2，…，βn，则方程组（8.16）又可写为
的形式.从而有如下定理：
定理8.7 线性方程组（8.16）有解的充分必要条件是b是列向量组β1，β2，…，βn的线性组合.
定理8.8 线性方程组（8.16）有解的充分必要条件是rankA=rank（A，b），即系数矩阵和增广矩阵有相等的秩.
对于每一个形如方程组（8.16）的线性方程组，都对应于一个齐次线性方程组Ax=0，称为线性方程组（8.16）对应的齐次线性方程组或者导出组.有如下线性方程组解的结构定理.
定理8.9 如果rankA=r，y0是n元线性方程组Ax=b的任意一个解.ξ1，ξ2，…，ξn-r是齐次线性方程组Ax=0的基础解系，则线性方程组Ax=b的全部解可以写成
y0+c1ξ1+c2ξ2+…+cn-rξn-r
的形式，这里c1，c2，…，cn-r是任意实数.
证明：显然，
y0+c1ξ1+c2ξ2+…+cn-rξn-r
一定是线性方程组Ax=b的解.同时，若y是Ax=b的解，则y-y0一定是Ax=0的解.故此定理成立.证毕.
这个定理8.9中出现的解y0称为该线性方程组的特解.(https://www.chuimin.cn)
例8.11 解线性方程组
解：对线性方程组的增广矩阵作初等行变换有
原方程组的等价方程组是
它的一个特解是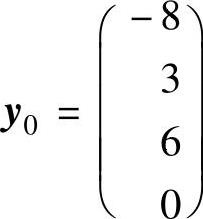
.原方程组对应的齐次方程组的基础解系是
，所以，原方程组的通解是
其中c是任意常数.
例8.12 解线性方程组
解：
由于系数矩阵的秩是2，但是增广矩阵的秩是3，所以这个方程组无解.
习题
8.4.1. 判断下列线性方程组是否有解，如果有解的话，求出线性方程组的全部解.
8.4.2. 设η∗是非齐次线性方程组Ax=b的一个解，η1，η2，…，ηs是对应的齐次线性方程组的一个基础解系.证明：η∗，η1，η2，…，ηs线性无关.
8.4.3. 设η1，η2，…，ηs是非齐次线性方程组Ax=b的s个解，k1，k2，…，ks是实数，且满足条件k1+k2+…+ks=1.证明：k1η1+k2η2+…+ksηs也是它的解.
8.4.4. 设非齐次线性方程组Ax=b的系数矩阵的秩为r，η1，η2，…，ηn-r+1是它的n-r+1个线性无关的解.证明：它的任意解可以表示为
x=k1η1+k2η2+…+kn-r+1ηn-r+1，
其中k1+k2+…+kn-r+1=1.
相关文章
- 详细阅读
-
数域中的高等代数，证明与习题解答详细阅读
，这说明零与负整数都属于F.至此可以得到整数集合ZF.再由除法的封闭性，以及任何有理数都可以写成两个整数的商，这样就得到有理数域QF.证毕.该定理表明，从包含关系上说有理数域是最小的数域.习题1.5.1. 证明：，都是无理数.1.5.2. 设p1，p2，…......
2025-09-30
- 详细阅读
-
高等代数中集合与其运算-高等代数详细阅读
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2025-09-30
-
高等代数：矩阵秩原理及应用详细阅读
解：是.由Am×r是列满秩矩阵，则存在行满秩矩阵Pr×m，使得PA=Er.在等式Am×rBr×n=Om×n两端左边乘P，则有Pr×m=Pr×mOm×n=Or×n及Br×n=ErBr×n=Br×n，比较两式可知B=O.是.显然有A（B-C）=O，利用的结论即得B-C=O.习题3.6.1. 如果AB，BA都是有意义的，那么它们是否具有相等的秩？，As都是n阶方阵，证明：并且等号可以取到.3.6.......
2025-09-30
-
线性映射结果及核-高等代数详细阅读
设σ是n维线性空间V1到m维线性空间V2的线性映射，即σ∈L.称集合{σ（α）|α∈V1}为线性映射σ的像空间，简称为像，记作Imσ；称集合{α|σ（α）=0}为线性映射σ的核空间，简称为核，记作kerσ.例5.4 在这个例子中，有Imσ=R2，kerσ=span（ε3）.例5.5 在这个例子中，有Imτ=span，kerτ={0}.例5.6 在这个例子中，有Imσ=S，kerσ=T.命题5.3 若向量组α1，α2，…......
2025-09-30
-
高等代数：实数域上的内积定义及性质详细阅读
定义6.1 在实数域R上的线性空间V中，定义一个二元函数V×V→R，称为向量α，β∈V的内积，记作<α，β>，如果下面几个条件同时成立：（1）<α，β>=<β，α>，对任意向量α，β∈V成立；（2）
2025-09-30
-
高等代数中的分块矩阵及其应用详细阅读
，As都是方阵，那么形如的分块矩阵称为分块对角矩阵，简称分块对角阵，可以简单地记作diag（A1，A2，…，Es）有下面的三种分块初等矩阵：E=diag（E1，…......
2025-09-30
相关推荐