，βn，则方程组又可写为的形式.从而有如下定理：定理8.7 线性方程组有解的充分必要条件是b是列向量组β1，β2，…，ηs是对应的齐次线性方程组的一个基础解系.证明：η，η1，η2，…+ksηs也是它的解.8.4.4. 设非齐次线性方程组Ax=b的系数矩阵的秩为r，η1，η2，…......
2023-11-22
高等代数：消元法解线性方程组
【摘要】：在第3章中，我们初步探讨了用消元法解线性方程组，现在对这一方法作一个较详细的讨论.考虑由m个n元一次线性方程组成的线性方程组为了得到方程组（8.1）的全部解，我们先想办法减少方程组中变量的个数.可以利用加减消元法或者代入消元法消去一些变量.例如，先消去变量x1.不失一般性地，不妨假定a11≠0，在第i个方程中减去第一个方程的倍，得到新方程ai2x2+ai3x3+…
在第3章中，我们初步探讨了用消元法解线性方程组，现在对这一方法作一个较详细的讨论.
考虑由m个n元一次线性方程组成的线性方程组
为了得到方程组（8.1）的全部解，我们先想办法减少方程组中变量的个数.可以利用加减消元法或者代入消元法消去一些变量.例如，先消去变量x1.不失一般性地，不妨假定a11≠0，在第i（2≤i≤m）个方程中减去第一个方程的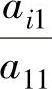
倍，得到新方程
a（1）i2x2+a（1）i3x3+…+a（1）inxn=bi（1），2≤i≤m，
即得到一个新方程组
如果我们可以得到方程组（8.2）的全部解，则必可通过方程组（8.1）中的第一个方程求出相应的变量x1，即得到方程组（8.1）的全部解.实际上，容易证明方程组（8.1）与方程组
同解（请读者自证）.这样求解方程组（8.1）的问题就转化为求解方程组（8.3）.
把方程组（8.3）重新记作
如果在方程组（8.4）中有矛盾的方程，则方程组（8.4）无解，进而方程组（8.1）必然无解.否则，在方程组（8.4）中，从第2到m个方程中再消去一个变量，不妨设可以消去x2，进行与上面类似的过程，可以得到一个与方程组（8.4）进而与方程组（8.1）同解的方程组
如果方程组中有矛盾方程，则必然无解.否则，从第3到m个方程中再消去一个变量，并如此进行下去，最终总可以把方程组化为如下形式
这里，a（r）11，a（r）22，…，a（r）rr都不是零.
容易得到，方程组（8.1）有解的充分必要条件是方程组（8.6）有解.并且当b（r）r+1，…，b（r）m至少有一个不是零时，方程组无解；当b（r）r+1=…=b（r）m=0时，方程组必然有解，且r=n时方程组有唯一的解，r<n时方程组有无穷多解.
在方程组（8.6）有解时，令
xr+1=k1，xr+2=k2，…，xn=kn-r，
可以通过代入法求得全部的变量x1，x2，…，xn，这里，k1，k2，…，kn-r是任意的值.(www.chuimin.cn)
这种通过消元求解方程组的方法称为高斯消元法.
例8.4 利用高斯消元法解方程组
解：消去变量x，化为同解方程组
显然，方程组无解.
例8.5 利用高斯消元法解方程组
解：方程组（8.7）消去变量x化为同解方程组
在方程组（8.8）中利用第二个方程消去后两个方程中的变量z，得到
在方程组（8.9）中利用第三个方程消去最后一个方程中的变量u，得到
令y=k1，v=k2，则可以依次解得
u=3-2k2，z=3-2k2，x=2k1+3k2-6，
即得方程组的解为
习题
8.2.1. 利用高斯消元法解下列方程组.
有关高等代数的文章
- 详细阅读
-
高等代数：线性方程组与矩阵详细阅读
，an，b是复数，则形如的方程称之为n元线性方程.由若干个n元线性方程组成的一组方程，称为线性方程组.能够使得线性方程组中所有方程同时成为等式的一组数值，称为方程组的一组解.下面我们初步探讨线性方程组的求解方法.例3.1若公鸡五文钱一只，母鸡三文钱一只，小鸡一文钱三只，现在用一百文钱买到一百只鸡，问：公鸡、母鸡、小鸡各买多少只？......
2023-11-22
-
高等代数中的齐次线性方程组详细阅读
形如的一组线性方程称为n元齐次线性方程组.其中，矩阵称为齐次线性方程组的系数矩阵.记x=（x1，x2，…，xn）T，则这个齐次线性方程组可以简单地记作Ax=0.显然，齐次线性方程组必然有一组解x=（0，0，…，bn）.如果线性方程组Ax=0......
2023-11-22
-
行列式计算：高等代数-高等代数详细阅读
，xn）.解此递推关系可以得到例9.15 计算n阶行列式.解：将这个行列式的每一列都拆为两列，进而把行列式分成2n个行列式之和.当n>2时，它们中的每一个都有两列成比例.因此，行列式等于零.当n=1时，行列式等于a1+b1.当n=2时，行列式等于.例9.16 设四阶方阵，计算行列式|A|.解：由于所以|A|2=|A||AT|=|AAT|=4.再因为|A|中a4的系数为正，所以，|A|=2.例9.17 计算n阶循环行列式.解：这里我们记，以ζk=ζk，k=1，2，…......
2023-11-22
-
高等代数中集合与其运算-高等代数详细阅读
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2023-11-22
-
高等代数：线性空间的定义详细阅读
定义4.1 设F是数域，V是一个非空集合，V中的元素具有两种运算，分别称为加法运算和数乘运算.所谓加法运算，就是一个对应法则，该法则使得集合V中任意两个元素α，β都对应于集合V中一个确定的元素γ，并称γ为元素α与β的和，记作γ=α+β.数乘运算是集合V中元素与数域F中的元素之间的运算法则，该法则使得集合V中任意一个元素α与数域F中任意一个数k，都对应于V中一个确定的元素δ，并称δ为k与α的数量乘积......
2023-11-22
- 详细阅读
-
高等代数：行列式理论的应用详细阅读
，n的一个排列，eγ是第γ分量为1，其余分量为0的n维列向量.再把行列式按前n-s列展开得由于=n2+s2-ns+2n-s，所以有又由于-=n（n+1）+s（s-1）-2ns是一个偶数，所以，n2+s2-ns+2n-s和ns+n有相同的奇偶性.从而得到定理9.19 设A，B分别是s×n，n×t阶矩阵，C=AB，r是一个正整数，则当r>n时，；当r≤n时，证明：利用矩阵乘法规则可以看到，从矩阵A中选出第i1，i2，…......
2023-11-22
相关推荐