高等代数：二次型标准形及变量代换

2023-11-22 理论教育版权反馈

【摘要】：对二次型f（x1，x2，…，xn）=xTAx，作一个线性的变量代换x=Cy，其中C是一个n阶方阵，得到f（x1，x2，…

对二次型f（x₁，x₂，…，x_n）=x^TAx，作一个线性的变量代换x=Cy，其中C是一个n阶方阵，得到

f（x₁，x₂，…，x_n）=x^TAx=y^T（C^TAC）y.

容易验证，矩阵C^TAC仍然是一个对称矩阵，因此，y^T（C^TAC）y依旧是二次型.这就是说，二次型经过变量的线性代换仍旧变为二次型.

显然，如果矩阵C是可逆的，那么，从x=Cy可以得到y=C^-1x，即变量x，y是可以互相表示的，并且这种表示是唯一的.这时，线性代换x=Cy称为可逆的.变换后的二次型的矩阵与原二次型的矩阵是合同的.

定义7.2 设A，B都是n阶对称矩阵，P是n阶可逆矩阵.如果

A=P^TBP，

那么称对称矩阵A与B是合同的.

命题7.1 矩阵的合同关系是一个等价关系，即合同关系具有下列三条性质：

（1）反身性对任何对称矩阵A，A与A合同；

（2）对称性对任何对称矩阵A，B，若A与B合同，则B与A合同；

（3）传递性对任何对称矩阵A，B，C，若A与B合同，B与C合同，则A与C也合同.

证明留作习题.

由推论3.2立即可以知道：

命题7.2 可逆的线性代换不改变二次型的秩，即合同的矩阵具有相同的秩.

一般形式的二次型是复杂的，其主要原因是由于大量的交叉乘积项使得我们难以把握二次型的性质.因此，借助某种类型的变换将二次型转化为一个形式简单的二次型是开始研究二次型的重要一步.利用初等配方法可以达到这个目的.

例7.3 求一个可逆的线性代换C，化二次型

f（x₁，x₂，x₃）=4x²₁+x²₂+x²₃-4x₁x₂-3x₂x₃+4x₃x₁

为只含平方项的形式.

解：使用配方法.

f（x₁，x₂，x₃）=4x²₁+x²₂+x²₃-4x₁x₂-3x₂x₃+4x₃x₁

=（4x²₁+x²₂+x²₃-4x₁x₂-2x₂x₃+4x₃x₁）-x₂x₃

=（2x₁-x₂+x₃）2-x₂x₃，

作线性代换

即

或者写为矩阵形式

这样，关于变量组x的二次型f可化为关于变量组y的二次型g：

g（y₁，y₂，y₃）=f（x₁，x₂，x₃）=y²₁-y₂y₃.

作线性代换

即

则可得

h（z₁，z₂，z₃）=f（x₁，x₂，x₃）=z²₁-z²₂+z²₃.

这样，作线性代换

也即

可将二次型f（x₁，x₂，x₃）化为关于变量组z₁，z₂，z₃的二次型z²₁-z²₂+z²₃.

例7.3表明，所谓利用可逆线性代换化二次型f为只含平方项的形式，其矩阵形式是找到一个可逆矩阵C，使得f的矩阵A通过矩阵C合同于一个对角形矩阵.由于每一个可逆矩阵都是一些初等方阵的乘积，而每一个初等方阵都对应于一种初等变换，因此，对二次型的配方过程可以通过矩阵的初等变换完成.矩阵的这种变换过程称为矩阵的合同变换.

若对称矩阵A与B合同，即存在可逆矩阵P使得B=P^TAP.这时，必然有初等矩阵P₁，P₂，…，P_s使得

P=P₁P₂…P_s.

因此，必然有下面的关系式：

B=P^T_sP^T_s-1…P^T₁AP₁…P_s-1P_s，

从矩阵运算的结合律，有

B=P^T_s（P^T_s-1…（P₂^T（P^T₁AP₁）P₂）…P_s-1）P_s. （7.1）

分析式（7.1）可以使我们引入矩阵的合同变换.对矩阵A的行施行一次初等变换之后，马上对列施以相同的初等变换，所得矩阵与A合同，矩阵的这种变换称为矩阵的合同变换.因此，矩阵A可以通过合同变换化为矩阵B.

依据这样的分析可以看出，若A是一个n阶对称矩阵，那么构造n×2n阶矩阵（A，E），并对这个矩阵施以合同变换，当A所在的块化为矩阵B时，单位矩阵E变换为矩阵P^T，这时必然有B=P^TAP.

例7.4 求可逆线性代换C化二次型

f（x₁，x₂，x₃）=-x₁x₂+2x₂x₃-3x₃x₁

为标准形.

解：首先，二次型f的矩阵为

下面对矩阵A作合同变换，使之化为对角形矩阵.

计算结果表明，取可逆矩阵

则二次型f在可逆线性代换X=CY之下化为二次型-2y²₁+2y²₂-6y²₃.这里的线性代换X=CY也就是

简单的计算还容易验证矩阵乘积

在进一步讨论之前，我们引入下列几个概念.

定义7.3 只含有平方项的二次型称为标准的，与二次型合同的只有平方项的二次型称为该二次型的标准形.在一个二次型的标准形中，平方项的个数称为这个二次型的秩；正平方项的个数称为这个二次型的正惯性指数，负平方项的个数称为这个二次型的负惯性指数，统称惯性指数；正惯性指数与负惯性指数的差称为这个二次型的符号差；所有平方项的系数都是1或者-1的标准形称为二次型的规范型.

我们的问题是一个二次型是否有标准形与规范型，如果有，它们是否唯一确定？本节下面的主要目的就是解决这两个问题.首先，我们给出主要的结果定理7.1与定理7.2.

定理7.1 任何n元二次型都能用可逆的线性代换化为只含有平方项的形式，且平方项的个数等于二次型的秩.

定理7.2 Sylvester惯性定律秩为r的二次型都能用可逆的线性代换化为规范形，且规范形中正负惯性指数是唯一确定的.

利用合同的概念，我们给出定理7.1与定理7.2的矩阵形式，并给出证明.

定理7.3 任何n阶对称方阵A都合同于一个对角形方阵，并且它们有相同的秩.

证明：可以看出这个定理是定理7.1的矩阵形式，命题7.2表明只需要证明前一半结论即可.

对矩阵A的阶数n用归纳法.

当n=1时，显然成立.

假设命题对n-1阶对称方阵都成立，则当A是n阶方阵时，我们分为三种情形进行讨论.

情形一 a₁₁≠0，把矩阵A写成分块矩阵形式：

这里A₁是一个n-1阶对称方阵，α是一个n-1维列向量.直接验证有等式

容易验证n-1阶矩阵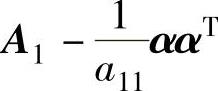是对称方阵.由归纳假设，存在n-1阶可逆矩阵P₁使得矩阵

是对角阵.

构造n阶方阵

则P为可逆矩阵，且P^TAP是对角形矩阵.(www.chuimin.cn)

情形二 a₁₁=0，但有某一a_1i≠0，不妨设a₁₂≠0，此时，取n阶方阵

则P^TAP仍然是对称方阵，且左上角元素变为a₁₂+a₂₁≠0，于是这种情况就转化为情形一.

情形三 a_1i=0，1≤i≤n，把A分块为分块矩阵：

其中，A₁是n-1阶对称方阵.由归纳假设，存在可逆阵P₁，使得P^T₁AP₁为对角阵.令n阶方阵

则P是可逆矩阵，且P^TAP是对角形矩阵.证毕.

定理7.4 任何n阶对称方阵A都合同于一个形如

的对角形矩阵，这里p，q都是唯一确定的，分别是矩阵A的正负惯性指数，而p+q是矩阵的秩.

证明：首先，通过简单的计算可以验证等式

E（i，j）diag（…，λ_i，…，λ_j，…）E（i，j）=diag（…，λ_j，…，λ_i，…）.

由定理7.3及上面简单的结果，可以知道，n阶对称方阵A都合同于一个形如

B=diag（λ₁，…，λ_p，-μ₁，…，-μ_q，0，…，0）

的对角形矩阵，其中0≤p，q≤n，p+q=rankA，λ_i，μ_j>0，1≤i≤p，1≤j≤q.作可逆矩阵

则C^T=C是对称矩阵且

这样，就证明了任意对称矩阵一定合同于一个对角形矩阵

下面证明该定理的后半部分，即正负惯性指数p，q的唯一性.

设n阶对称矩阵A与方阵

都合同，由于合同是等价关系，因此矩阵S₁与S₂合同.故只需证明p=p′且q=q′即可.

由于合同的矩阵具有相同的秩，因此，p+q=p′+q′.若P是可逆方阵，且使得P^TS₁P=S₂.把S₁与S₂分别分块为

其中T₁，T₂都是p+q阶方阵；并把矩阵P按相同的方式分块为分块矩阵

则就有等式

即

比较得P^T₁T₁P₁=T₂，即矩阵T₁与矩阵T₂合同.

如果p>0且p′>0，把矩阵T₁，T₂分别分块为

并把矩阵P₁按相同的方式分块为分块矩阵

其中，α，β都是列向量.由于有P^T₁T₁P₁=T₂，也就是

即等式

比较得

取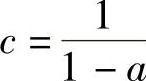或（只要有意义即可），记Q₁=cβα^T，则有

（1-a²）c²-2ac=1

及

Q^T₁U₁Q₁+Q^T₁U₁Q+Q^TU₁Q₁

=c²αβ^TU₁βα^T+cαβ^TU₁Q+cQ^TU₁βα^T

=（1-a²）c²αα^T-acαα^T-acαα^T

=[（1-a²）c²-2ac]αα^T

=αα^T.

进一步可以得到

U₂=Q^TU₁Q+αα^T

=Q^TU₁Q+Q^TU₁Q₁+Q^T₁U₁Q+Q^T₁U₁Q₁

=（Q+Q₁）^TU₁（Q+Q₁）.

由于矩阵U₂可逆，因此，U₁与U₂合同.

下面来证明p=p′，进而有q=q′.如果p<p′，由P^T₁T₁P₁=T₂，反复使用上面的结论p次，将得到-E_q与矩阵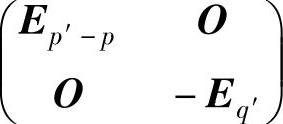合同，即存在可逆矩阵P₀，使得

显见，对任意q维向量x，

-x^TP₀^TP₀x=-（P₀x）^T（P₀x）≤0.

但是，对q维向量x₀=（1，0，…，0）T，有

矛盾.因此p≥p′，同理p≤p′，因此p=p′.证毕.

在上一章中，我们知道，如果对称矩阵A的特征值为λ₁，λ₂，…，λ_n，则存在正交矩阵O，使得O^-1AO=diag（λ₁，λ₂，…，λ_n），由于O^-1=O^T，所以O^TAO=diag（λ₁，λ₂，…，λ_n）.于是，我们得到对称矩阵在合同关系下的标准形.

定理7.5 若对称矩阵A的特征值是λ₁，λ₂，…，λ_n，则存在正交矩阵O，使得

O^TAO=diag（λ₁，λ₂，…，λ_n）.

定理7.6 若对称矩阵A的特征值是λ₁，λ₂，…，λ_n，则存在正交变换x=Oy，使得二次型f（x）=x^TAx化为标准形

λ₁y²₁+λ₂y²₂+…λ_ny²_n.

习题

7.2.1. 求出可逆的线性代换C，化下面二次型为标准形，并求出规范形、秩、惯性指数及符号差.

（1）x²₁+2x²₂-x²₃+2x₁x₂-2x₃x₁；

（2）2x₁x₂+2x₂x₃+2x₃x₁；

（3）x²₁-x²₂+2x₁x₂+4x₃x₁；

7.2.2. 证明命题7.1.

7.2.3. 证明秩为r的对称矩阵可以写成r个秩为1的对称矩阵的和.

7.2.4. 对二次型x^TAx，如果存在列向量α，β，使得α^TAα<0，且β^TAβ>0，则一定存在列向量γ≠0，使得γ^TAγ=0.

7.2.5. 证明：一个二次型可以分解为两个实系数的一次齐次多项式的乘积的充分必要条件是它的秩等于1，或者秩等于2及符号差等于0.

7.2.6.设a，b是实数，求出二次型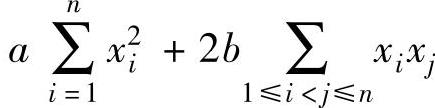的秩和惯性指数.

7.2.7. 设A是对称矩阵，求证：存在一个正实数c，使得对任意列向量α，都有|α^TAα|≤cα^Tα.

7.2.8. 设A是对称矩阵，证明：存在对称矩阵B，使得A=B³.

7.2.9. 把合同的二次型看作在不同基下的表示，给定理7.4唯一性部分一个简单证明.

7.2.10. （Witt）设S₁，T₁是n阶对称矩阵，S₂，T₂是m阶对称矩阵，

若S与T合同，S₁与T₁合同，证明：S₂与T₂也合同.

7.2.11.设A是n阶反对称矩阵，证明：存在可逆矩阵P，使得

7.2.12.证明：反对称矩阵的特征值都是纯虚数.

高等代数：二次型标准形及变量代换

相关推荐