+a1α+a0∈F称为多项式f在x=α处的值，记作f（α）=anαn+an-1αn-1+…，αn+1是n次多项式f的不同的根.显然，x-αi一定两两互素，因此，f=q…，考虑多项式两端的次数可以看到只有f=0.证毕.推论2.6 若两个n次多项式在n+1个不同的点取值相同，则它们必相等.证明：设f，g是数域F上的n次多项式，且在n+1个不同的点αi，i=1，2，…......
2025-09-30
标准正交基在高等代数中的重要性
【摘要】：，αs线性无关.证毕.命题6.4说明在n维欧氏空间中不可能找到n+1个两两正交的非零向量.定义6.4 在n维欧氏空间中，由n个向量组成的正交向量组是一组基，称为正交基.由单位向量组成的正交基，称为标准正交基.在n维欧氏空间V中，任选一组基α1，α2，…，αn出发，一定可以构造一组标准正交基β01，β02，…+xnyn.这个结果表明，在欧氏空间中内积是唯一确定的.另选一组标准正交基η1，η2，…
如果欧氏空间V中的一组非零向量α1，α2，…，αs两两正交，则称为正交向量组.
命题6.4 正交向量组一定是线性无关的.
证明：若α1，α2，…，αs是正交向量组，它们的线性组合
β=k1α1+k2α2+…+ksαs=0.
将向量β与每个向量αi作内积，则有
0=<β，αi>=ki<αi，αi>，
又αi≠0，则ki=0，即α1，α2，…，αs线性无关.证毕.
命题6.4说明在n维欧氏空间中不可能找到n+1个两两正交的非零向量.
定义6.4 在n维欧氏空间中，由n个向量组成的正交向量组是一组基，称为正交基.由单位向量组成的正交基，称为标准正交基.
在n维欧氏空间V中，任选一组基α1，α2，…，αn，可以从它出发来构造一个标准正交基.
首先，令β1=α1，β2=α2+kα1，使得<β1，β2>=0，可得
因此向量
满足条件β1，β2正交，并且
span（α1，α2）=span（β1，β2）.
令β3=α3+kβ1+lβ2，且β1，β2，β3两两正交，则有
<β1，β3>=0，<β2，β3>=0，
从中解得
此时，β1，β2，β3两两正交，且
span（α1，α2，α3）=span（β1，β2，β3）.
一般地，若β1，β2，…，βi已两两正交，则向量
与它们正交，并且满足条件
span（α1，α2，…，αi+1）=span（β1，β2，…，βi+1）.
如此继续，可得正交向量组β1，β2，…，βn，且
span（α1，α2，…，αn）=span（β1，β2，…，βn）.
上面由基α1，α2，…，αn得到两两正交的基β1，β2，…，βn的方法称为Gram-Schmidt正交化方法.将得到的向量组β单位化，这样就证明了下面定理：
定理6.1 在n维欧氏空间V中，从任意一组基α1，α2，…，αn出发，一定可以构造一组标准正交基β01，β02，…，β0n，并且这组基还满足：
span（β01，β02，…，β0i）=span（α1，α2，…，αi），i=1，2，…，n.
推论6.1n维欧氏空间V恒存在标准正交基.
推论6.2n维欧氏空间V的任意一个正交向量组恒可扩充为一组V的正交基.特别地，任意一个单位向量都可以扩充成一组标准正交基.
例6.7 在三维空间R3中，设
α1=（1，1，0），α2=（1，0，-1），α3=（0，-1，1）.
首先，令β1=α1=（1，1，0），β2=α2+kβ1，且<β1，β2>=0，则有
0=<β1，β2>=<α1，α2+kβ1>=<α1，α2>+k<α1，α1>=1+2k，
从中解得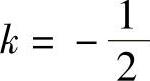
，则有
.
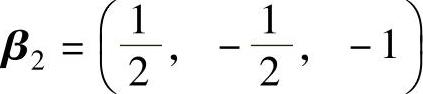再令β3=α3+kβ1+lβ2，且
<β3，β1>=<β3，β2>=0，
则有
解得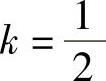
，
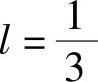，则有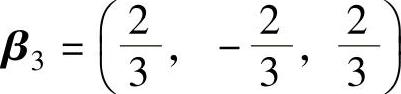
.
最后单位化，得到一组标准正交基：
例6.8 在闭区间[0，1]上考虑R上的线性空间R2[x]，内积定义为
<f（x），g（x）>=∫01f（x）g（x）dx.
取一组基α1=1，α2=x，α3=x2.
令β1=α1=1，β2=α2+kβ1，且<β1，β2>=0，则有
解得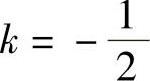
，则有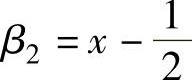
.
再令β3=α3+kβ1+lβ2，且(https://www.chuimin.cn)
<β3，β1>=<β3，β2>=0，
则有
解得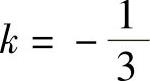
，l=-1，则有
.
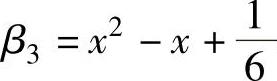最后单位化，得
例6.9 （正交化过程的几何意义）在二维欧氏空间R2上，取两个向量
α1=（4，2），α2=（1，3），
利用Gram-Schmidt正交化方法可得
β1=（4，2），β2=α2+kβ1=（-1，2），
其中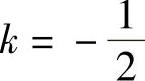
.这里向量-kβ1是向量α2在向量β1上的投影.因此，正交化方法的实质是求出向量在已知正交向量组及其垂直方向上的分解.
若ε1，ε2，…，εn是一组标准正交基，这时度量矩阵为单位矩阵
A=（<εi，εj>）=E.
设向量α的坐标是x，向量β的坐标是y，则易见
<α，β>=xyT=x1y1+x2y2+…+xnyn.
这个结果表明，在欧氏空间中内积是唯一确定的.
另选一组标准正交基η1，η2，…，ηn，由η1，η2，…，ηn到ε1，ε2，…，εn的过渡矩阵是O，由于在不同基下的度量矩阵是合同的，则有OTO=E.因此，OTO=OOT=E.
定义6.5n阶方阵O，如果满足条件
OTO=OOT=E，
则O称为正交矩阵.
从正交矩阵的定义可以马上得到：
定理6.2 若矩阵A是n阶方阵，那么下面条件等价：
（1）A是正交矩阵；
（2）A的行向量组构成标准正交基；
（3）A的列向量组构成标准正交基.
习题
6.2.1. 在线性空间R4中，计算向量α，β的夹角.
（1）α=（1，2，2，0）T，β=（-2，0，1，2）T；
（2）α=（0，-3，1，0）T，β=（1，-1，2，-2）T.
6.2.2. 利用Gram-Schmidt正交化方法把下列向量组正交化.
（1）α1=（1，1，1），α2=（1，2，3），α3=（1，4，9）；
（2）α1=（1，0，-1，1），α2=（1，-1，0，1），α3=（-1，1，1，0）.
6.2.3. 设ε1，ε2，…，εn是V的标准正交基，P为正交矩阵，
（η1，η2，…，ηn）=（ε1，ε2，…，εn）P，
问η1，η2，…，ηn是否为标准正交基？为什么？
6.2.4. 设ε1，ε2，ε3是R3中的一组标准正交基，证明：
也是一组标准正交基.
6.2.5. 构造R3的一组标准正交基，使它包含向量
6.2.6. 证明：
（1）正交矩阵的实特征值只能是±1；
（2）正交矩阵的特征值的绝对值一定是1.
6.2.7. 设AT=A，BT=-B且A-B可逆，AB=BA，证明：
（A+B）（A-B）-1
是正交矩阵.
6.2.8. 设A是n阶方阵，且A的特征值不等于0或-1.证明：A及A+E都可逆，且A是正交矩阵的充分必要条件是
（A+E）-1+（AT+E）-1=E.
相关文章
- 详细阅读
-
余弦正交基简介及在音视频压缩中的应用详细阅读
对于长度为N的一维信号X，余弦变换定义TC为TC=CN·X 正弦正交基元素由下列函数生成：由式确定的变换称为离散余弦变换。可通过近似为整数后变换，称为整数DCT，在H.264及AVS标准中被使用。对于4阶DCT，余弦变换基等于：式中，c=2cos（π/8）和s=sin（π/8）。余弦变换主要应用在数据内插、图像压缩方面，在MPEG-2、H.264、AVS等音视频压缩标准中得到了广泛应用。......
2025-09-29
-
高等代数中集合与其运算-高等代数详细阅读
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2025-09-30
-
标准物质在分析测试中的重要性详细阅读
标准物质具有测量标准的属性，在分析测试中起着量值传递、评价分析方法和分析质量控制等作用。对于标准物质，尤其是有证标准物质，广泛用于以下目的［6］。在日常化学分析中，采用相应的标准物质校准分析仪器的测量参数，实现量值的传递是简便和可靠的选择。例如，利用与样品基质相匹配且浓度相近的有证标准物质评价分析方法的偏倚（正确度）。......
2025-09-29
-
高等代数中的线性映射与矩阵表示详细阅读
，αn是V1的一组基，则只需确定它们在线性映射σ之下的像σ（α1），σ（α2），…，βm，若σ是从线性空间V1到V2的线性映射，由于σ（αj）∈V2，因此即这组关系可以用矩阵形式表示为今后把向量（σ（α1），σ（α2），…......
2025-09-30
-
了解沃尔什正交基详细阅读
图4-14 阶沃尔什基函数对于N阶沃尔什变换基，定义在N点间隔内过零次数的一半定义为列率。由表4-1可看出，按列率排列的沃尔什基序号k是过零次数，故对应列率k/2；反之，沃尔什基的沃尔什变换是仅在列率为k/2时非零的N向量。性质1：两个不同列率的沃尔什基形成完备正交系，即基相乘产生列率搬移。表4-2 N=8列率搬移性质2：信号并元移位s的沃尔什变换等于信号沃尔什变换与列率s和沃尔什基乘积。......
2025-09-29
-
向量组的标准正交化与正交矩阵解析详细阅读
+anbn=0时，称α与β正交.2.向量组的单位正交化单位正交向量组设α1，α2，…，αm单位正交化的施密特方法如下：（ⅰ）正交化：取β1=α1，（ⅱ）单位化：由此得到的ε1，ε2，…......
2025-09-30
- 详细阅读
相关推荐