高等代数：特征值与特征向量的计算

2025-09-30 理论教育版权反馈

【摘要】：，λs是线性变换σ的s个不同的特征值，Ti是属于特征值λi的线性无关的特征向量组成的向量组，则向量组T1∪T2∪…，αiri线性无关，1≤i≤s，并且满足条件σ（αij）=λiαij，1≤i≤s，1≤j≤ri.下面来证明向量组是线性无关的.若有一组组合系数kij使得记向量，1≤i≤s，由于这表明，若αi≠0，则αi是属于特征值λi的特征向量，由定理5.7可知向量组α1，α2，…

定理5.6表明，当线性空间可以写为一些不变子空间的直和的时候，线性变换的矩阵会具有较为简单的形式.本节将进一步研究这个问题.首先再来看一下线性变换及其矩阵之间的联系.

设V是数域F上的n维线性空间，σ∈L（V）是其上的一个线性变换.在选定基α₁，α₂，…，α_n之下，线性变换σ的矩阵是A.任取V中的向量

则有

这就是说，如果向量α的坐标是

那么，σ（α）的坐标就是Ax.这也就是说，在给定线性空间的基之后，对线性变换的研究就可以转化为对其矩阵的研究.

设σ是线性空间V上的线性变换，我们更感兴趣的是在线性变换σ之下，像与原像共线的那些向量.

定义5.4 设V是数域F上的线性空间，σ是V上的线性变换，如果存在复数λ∈F及V中非零向量α≠0，使得

σ（α）=λα，

则称λ为线性变换σ的特征值，相应的非零向量α称为属于特征值λ的特征向量.

由前面的分析可见，σ（α）=λα相当于Ax=λx，因此，也称λ是方阵A的特征值，非零向量x称为方阵A的属于特征值λ的特征向量.

例5.19 设V=R²是实数域R上的二维线性空间，α₁，α₂是V的一组基.σ是V上的线性变换，且满足条件

σ（α₁）=3α₁-2α₂，σ（α₂）=α_1.

σ有两个特征值1和2，向量α₁-2α₂是属于特征值1的特征向量；向量α₁-α₂是属于特征值2的特征向量.

如果记α=α₁-α₂，则集合{kα|k∈R}中的非零向量都是特征值2的特征向量，称为特征值2的特征子空间.一般地，

定义5.5 若σ是线性空间V上的线性变换，λ是σ的一个特征值，集合

{ασ（α）=λα，α∈V}

是V的一个线性子空间，称为属于λ的特征子空间，记作V_λ.特征子空间V_λ的维数称为特征值λ的几何重数.

例5.20 特征子空间一定是不变子空间.

例5.21 设σ是线性空间V上的线性变换，且满足σ²=σ，即σ为幂等变换.若λ是σ的特征值，α是属于特征值λ的特征向量，则σ（α）=λα.由于

σ²（α）=σ（σ（α））=σ（λα）=λσ（α）=λ²α

及

σ²（α）=σ（α）=λα，

比较得λ²α=λα，由α≠0，知λ²=λ，即λ=1或λ=0.这说明幂等变换的特征值只能是0或1.

例5.22 （续例5.21）由第三节例5.12我们知道，一定存在一组基α₁，α₂，…，α_n，使得σ在这组基下的矩阵是

其中r是线性变换σ的秩.或者说，在这组基之下有

即

σ（α_i）=α_i，1≤i≤r

σ（α_i）=0，r+1≤i≤n.

由此，同样可以得到σ的特征值只能是0或1.并且有特征子空间V₀的维数是n-r，V₁的维数是r，且有直和分解

V=V₀⊕V₁，

这一分解式恰好又可以写成

V=kerσ⊕Imσ.

注意：这样的分解一般不成立.甚至于，还可以有直和分解式

这一平凡分解的重要意义在于每一个子空间span（α_i），1≤i≤n，都是σ的一维不变子空间.

定理5.7 若α₁，α₂，…，α_s是分别属于λ₁，λ₂，…，λ_s的特征向量，且λ_i两两不等，则有向量组α₁，α₂，…，α_s一定是线性无关的.

证明：对向量组的向量个数s用归纳法，当s=1时，命题显然成立.

假设命题对s已成立，则对s+1，设α₁，α₂，…，α_s+1的线性组合

k₁α₁+k₂α₂+…+k_s+1α_s+1=0，（5.1）

则有

0=σ（k₁α₁+k₂α₂+…+k_s+1α_s+1）

=k₁σ（α₁）+k₂σ（α₂）+…+k_s+1σ（α_s+1）

=k₁λ₁α₁+k₂λ₂α₂+…+k_s+1λ_s+1α_s+1. （5.2）

如果有某一个λ_i=0，不妨设为λ_s+1=0，由式（5.2）有

k₁λ₁α₁+k₂λ₂α₂+…+k_sλ_sα_s=0，

利用归纳假设可以知道，α₁，α₂，…，α_s线性无关，因此k_iλ_i=0，即得k_i=0，1≤i≤s，于是k_s+1=0，这样就证明了向量组α₁，α₂，…，α_s+1是线性无关的.

如果所有的λ_i≠0，则利用式（5.2）-式（5.1）×λ_s+1，消去α_s+1有(https://www.chuimin.cn)

k₁（λ₁-λ_s+1）α₁+k₂（λ₂-λ_s+1）α₂+…+k_s（λ_s-λ_s+1）α_s=0，

同样可以得到k_i（λ_i-λ_s+1）=0，所以k_i=0，1≤i≤s，进而有k_s+1=0.这样也有向量组α₁，α₂，…，α_s+1是线性无关的.证毕.

定理5.8 若λ₁，λ₂，…，λ_s是线性变换σ的s个不同的特征值，T_i是属于特征值λ_i的线性无关的特征向量组成的向量组，则向量组

T₁∪T₂∪…∪T_s

一定是线性无关向量组.

证明：设向量组T_i为

那么，由条件知道向量组α_i1，α_i2，…，α_iri线性无关，1≤i≤s，并且满足条件

σ（α_ij）=λ_iα_ij，1≤i≤s，1≤j≤r_i.

下面来证明向量组

是线性无关的.若有一组组合系数k_ij使得

记向量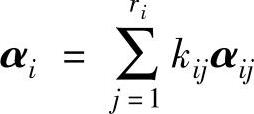，1≤i≤s，由于

这表明，若α_i≠0，则α_i是属于特征值λ_i的特征向量，由定理5.7可知向量组α₁，α₂，…，α_r线性无关.但是式（5.4）表明

α₁+α₂+…+α_s=0.

故此只能有所有α_i=0，1≤i≤s.因此

由条件可见

k_ij=0，1≤i≤s，1≤j≤r_i.

由线性无关的定义可知向量组（5.3）线性无关.证毕.

在特征子空间V_λ中，取定一组基α₁，α₂，…，α_r，并扩充为V的基α₁，α₂，…，α_n之后，线性变换σ在这组基下的矩阵应具有形式

在其左上角位置具有对角阵的形式，这使我们考虑如下问题：对于线性变换σ，是否存在一组基，使得σ在这组基下的矩阵是对角形矩阵.一般来说，这个问题的答案是否定的，但是有如下定理.

定理5.9 线性变换σ在某一组基下的矩阵是对角形矩阵的充分必要条件是它有n个线性无关的特征向量.

证明：必要性，若线性变换σ在基α₁，α₂，…，α_n下的矩阵是对角阵

diag（λ₁，λ₂，…，λ_n），

这里的λ_i有可能相同，则有

也就是说，

σ（α_i）=λ_iα_i，1≤i≤n.

充分性，若线性变换σ有n个线性无关的特征向量α₁，α₂，…，α_n，它们所属的特征值分别是λ₁，λ₂，…，λ_n，λ_i有可能相同，则

σ（α_i）=λ_iα_i，1≤i≤n，

此即

证毕.

推论5.1 若线性变换σ有n个不同的特征值，则σ在某组基下的矩阵是对角阵.

由于线性变换在不同基下的矩阵是相似的，因此，寻求一组基使得线性变换在这组基下的矩阵是对角阵的问题，就转化为判断某一矩阵是否可以和一个对角阵相似的问题，称之为矩阵的对角化问题.找到与一个矩阵相似的对角形矩阵的过程称为把该矩阵对角化.

注意到线性变换与其矩阵之间的对应关系，前面的定理用矩阵的形式写出就是：

定理5.10A是n阶方阵，则属于A的不同特征值的特征向量是线性无关的.

定理5.11A是n阶方阵，则A相似于一个对角阵的充分必要条件是A有n个线性无关的特征向量.

推论5.2 如果A有n个不同的特征值，则A一定相似于一个对角阵.

习题

5.5.1. 设λ₁，λ₂是线性变换σ的两个不同的特征值，ε₁，ε₂是分别属于λ₁，λ₂的特征向量，则ε₁+ε₂不是σ的特征向量.

5.5.2. 若σ是n维线性空间V上的线性变换，则V的任意子空间都是σ的不变子空间的充分必要条件是σ是纯量变换.

5.5.3. 设σ是线性空间V的可逆变换，证明：

（1）σ的特征值一定不是零；

（2）若λ是σ的特征值，则λ^-1一定是σ^-1的特征值.

5.5.4. 证明：幂零变换的特征值一定是零.

5.5.5. 证明：对合变换的特征值只能是1或-1.

5.5.6. 利用矩阵的方法证明定理5.10.

5.5.7. 利用矩阵的方法证明定理5.11以及推论5.2.

高等代数：特征值与特征向量的计算

相关推荐