线性变换概念及相似关系证明

2023-11-22 理论教育版权反馈

【摘要】：，αn）BA.证明留作习题.定义5.2 设A，B都是n阶方阵，如果存在n阶可逆方阵P，使得A=P-1BP，则称方阵A与方阵B相似.命题5.6 矩阵的相似关系是一个等价关系，即反身性矩阵A和它自身相似；对称性如果矩阵A和B相似，则矩阵B和A也相似；传递性如果矩阵A和B相似，矩阵B和C相似，则矩阵A和C也相似.证明留作习题.设σ是一个V上的线性变换，先取V的一组基α1，α2，…

n维线性空间V到自身上的线性映射，称为线性变换，这时通常把L（V，V）记作L（V）.

若V是数域F上的n维线性空间，选取V的一组基α₁，α₂，…，α_n，线性变换σ∈L（V）在选定这组基之下的矩阵是n阶方阵A.由定理5.1可以知道，

L（V）≅M_n（F）.

设σ，τ∈L（V），k∈R，可以用如下方式定义σ，τ的和、数乘、乘积如下：

（σ+τ）α≜σ（α）+τ（α），

（kσ）α≜kσ（α），

（τσ）α≜τ（σ（α））.

命题5.5 设V是n维线性空间，

α₁，α₂，…，α_n

是V的一组基，σ，τ∈L（V）在这组基下的矩阵分别是A，B，即

σ（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）A，

τ（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）B，

则有

（σ+τ）（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）（A+B），

（kσ）（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）kA，

（τσ）（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）BA.

证明留作习题.

定义5.2 设A，B都是n阶方阵，如果存在n阶可逆方阵P，使得A=P^-1BP，则称方阵A与方阵B相似.

命题5.6 矩阵的相似关系是一个等价关系，即

（1）反身性矩阵A和它自身相似；

（2）对称性如果矩阵A和B相似，则矩阵B和A也相似；

（3）传递性如果矩阵A和B相似，矩阵B和C相似，则矩阵A和C也相似.

证明留作习题.

设σ是一个V上的线性变换，先取V的一组基α₁，α₂，…，α_n，σ在这组基下的矩阵为A，即

σ（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）A.

另取V的一组基β₁，β₂，…，β_n，σ在这组基下的矩阵是B，即

σ（β₁，β₂，…，β_n）=（β₁，β₂，…，β_n）B.

设从基β₁，β₂，…，β_n到基α₁，α₂，…，α_n的过渡矩阵是P，即

（α₁，α₂，…，α_n）=（β₁，β₂，…，β_n）P.

由上可以得到

σ（α₁，α₂，…，α_n）=σ[（β₁，β₂，…，β_n）P]

=[σ（β₁，β₂，…，β_n）]P

=（β₁，β₂，…，β_n）BP

=（α₁，α₂，…，α_n）P^-1BP.

比较可得

A=P^-1BP.

即同一线性变换在不同基下的矩阵是相似的.

反之容易看到，若矩阵A，B相似，而线性变换σ在某一组基下的矩阵是B，则可以找到一组基，使得σ在这组基下的矩阵是A.

若线性变换σ是1—1映射，则称之为可逆变换，可逆变换把一组基变为一组基，并且逆变换的矩阵就是变换的矩阵的逆.

命题5.7 设α₁，α₂，…，α_n是n维线性空间V的一组基，σ是V的可逆线性变换，且

σ（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）A，

则有A是可逆方阵，且

σ^-1（α₁，α₂，…，α_n）=（α₁，α₂，…，α_n）A^-1.

证明留作习题.

定理5.5 设σ是n维线性空间V上的线性变换，则下述条件等价：

（1）σ是可逆变换；

（2）σ的矩阵是可逆矩阵；

（3）kerσ={0}；

（4）Imσ=V.

这个定理的证明留作习题.

以下总设V是n维线性空间.

例5.9 设σ∈L（V）是线性变换，且σ（α）=0对所有的α∈V都成立，则σ的矩阵是零方阵，称这个线性变换σ为零变换，记为θ或0.此时，Imσ={0}，kerσ=V.

例5.10 设σ∈L（V）是线性变换，且σ（α）=α对所有的α∈V都成立，称这个线性变换σ为恒等变换，通常把恒等变换记作ι，其矩阵是单位矩阵E_n.此时，Imι=V，kerι={0}.而且，对于V上任意的线性变换τ，都有ιτ=τι=τ.

例5.11 设σ∈L（V）是线性变换，且存在一组基α₁，α₂，…，α_n，使得(www.chuimin.cn)

σ（α_i）=λ_iα_i，λi∈F，1≤i≤n，

称这个线性变换σ为仿射变换，其矩阵是对角形矩阵

当所有的λ_i≠0时，σ还是可逆的.当所有的λ_i都相等为λ时，称为数乘变换或纯量变换，这时的矩阵为λE.

例5.12 设σ∈L（V）是线性变换，且满足σ²=σ，这样的线性变换称为幂等变换.若σ的矩阵为A，易得A²=A，即A是幂等阵.由第2章结果知A相似于对角阵

再由本节的讨论知，如果σ是幂等变换，则一定存在一组基，使得σ在这组基下的矩阵是

例5.13 设σ∈L（V）是线性变换，且满足σ²=ι，则称为对合变换.

简单计算可以验证线性变换σ²=ι等价于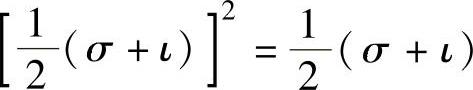.也就是说，线性变换σ是对合变换的充分必要条件是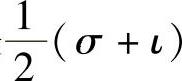是幂等变换.由例5.12一定存在V中一组基使得线性变换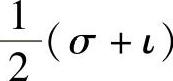在这组基之下的矩阵A满足：

从中可以得出线性变换σ的矩阵为

其中r=rank（A+E）.

这里的全部结果用矩阵的语言说就是，若A是n阶方阵，那么A是对合矩阵的充分必要条件是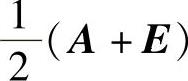是幂等矩阵；对合矩阵一定相似于对角阵

其中r=rank（A+E）；若A是对合矩阵，那么必有

rank（A+E）+rank（A-E）=n.

例5.14 设σ∈L（V）是线性变换，且存在自然数k，满足σ^k=0，则这个线性变换σ称为幂零变换，其矩阵A满足A^k=O是幂零矩阵.

例如，取一组基α₁，α₂，…，α_n，可以建立这样一个线性变换σ：V→V，使得

σ（α₁）=O，σ（α_i）=α_i-1，2≤i≤n，

则这个线性变换σ的矩阵为

验算易得，A^n-1=O，即知σ^n-1=0.此时必然有

Imσ=span（α₁，α₂，…，α_n-1），kerσ=span（α₁）.

从这个例子中可以看到，尽管

dim Imσ+dim kerσ=n，

但是

Imσ+kerσ≠V.

例5.15 若映射σ：R_n-1[x]→R_n-1[x]，σ（f（x））=f′（x），则容易验证σ是线性变换.由于σⁿ=0，因此，σ是幂零变换.易得

Imσ=R_n-1[x]，kerσ=R.

习题

5.3.1. 判断下面定义的变换，哪些是线性的.

（1）在线性空间V中，σ（α）=α+α₀，α₀是V中一个固定的向量；

（2）在线性空间V中，σ（α）=α₀，α₀是V中一个固定的向量；

（3）在线性空间R³中，σ（（x₁，x₂，x₃））=（2x₁-x₂，x₂+x₃，x₁）；

（4）在M_n（R）中，σ（X）=AXB，A，B固定的n阶方阵.

5.3.2. 证明命题5.5～命题5.7.

5.3.3. 证明定理5.5.

5.3.4. 设σ是线性空间V上的线性变换，如果σ^k（α）=0，但是σ^k-1（α）≠0.证明：向量组

α，σ（α），…，σ^k-1（α）

是线性无关的.

5.3.5. 设σ是n维线性空间V上的线性变换，α∈V，且σⁿ（α）=0，但是σ^-1（α）≠0.证明：线性变换σ在某组基下的矩阵是

5.3.6. 续例5.14，对每个自然数k，计算：Imσ^k及kerσ^k.

5.3.7. 设A是n阶幂零阵，且k是使得A^k=0的最小的自然数，证明：k≤n.

5.3.8. 在线性空间M₂（R）中，设

σ是M₂（R）上的线性变换，满足条件σ（X）=XA-AX，计算：Imσ，kerσ.

5.3.9. 设σ是线性空间V上的线性变换，证明：Imσ⊆kerσ的充分必要条件是σ²=0.

5.3.10. 设σ是线性空间V上的线性变换，证明：

（1）存在自然数k，使得kerσ^k=kerσ^k+1；

（2）存在自然数k，使得Imσ^k=Imσ^k+1.

5.3.11. 设S，T是n维线性空间V的子空间，且V=S⊕T.证明：存在唯一的幂等变换σ，使得Imσ=S且kerσ=T.

5.3.12. 若σ，τ是n维线性空间V的线性变换，则στ-τσ不可能是恒等变换.

5.3.13. 若σ，τ是幂等的线性变换，证明：

（1）如果σ+τ是幂等变换，则στ=0；

（2）如果σ，τ是可换的，即στ=τσ，则σ+τ-στ是幂等变换.

5.3.14. 设σ，τ是幂等的线性变换，证明：

（1）Imσ=Imτ的充分必要条件是στ=τ且τσ=σ；

（2）kerσ=kerτ的充分必要条件是στ=σ且τσ=τ.

线性变换概念及相似关系证明

相关推荐