设σ是n维线性空间V1到m维线性空间V2的线性映射,即σ∈L.称集合{σ(α)|α∈V1}为线性映射σ的像空间,简称为像,记作Imσ;称集合{α|σ(α)=0}为线性映射σ的核空间,简称为核,记作kerσ.例5.4 在这个例子中,有Imσ=R2,kerσ=span(ε3).例5.5 在这个例子中,有Imτ=span,kerτ={0}.例5.6 在这个例子中,有Imσ=S,kerσ=T.命题5.3 若向量组α1,α2,…......
2023-11-22
定义5.1 若V1,V2分别是数域F上的n维与m维线性空间,σ是从V1到V2的一个映射,且满足条件:
(1)对任意的向量α,β∈V1,都有σ(α+β)=σ(α)+σ(β);
(2)对任意的向量α∈V1以及数k∈F,都有σ(kα)=kσ(α),则称映射σ是一个从线性空间V1到线性空间V2上的线性映射.
线性映射是线性空间之间保持线性运算关系的一种映射.由定义可以知道线性映射有如下的简单性质.
命题5.1 若σ是一个从线性空间V1到V2的线性映射,则有
σ(0)=0,σ(-α)=-σ(α).
证明:由线性映射的定义中的条件(1)有
σ(0)=σ(0+0)=σ(0)+σ(0),
因此,σ(0)=0.
又由于
0=σ(0)=σ[α+(-α)]=σ(α)+σ(-α),
因此,σ(-α)=-σ(α).证毕.
命题5.2 线性映射保持线性运算关系不变.即对任意向量组
α1,α2,…,αs∈V1
以及任意一组组合系数k1,k2,…,ks∈F,总有
σ(k1α1+k2α2+…+ksαs)=k1σ(α1)+k2σ(α2)+…+ksσ(αs).
由定义5.1及数学归纳法就可以证明这个命题.
由命题5.2可见,若α1,α2,…,αn是V1的一组基,则只需确定它们在线性映射σ之下的像σ(α1),σ(α2),…,σ(αn),即可完全确定线性映射σ.
设V1,V2分别是n,m维线性空间,取定V1的一组基α1,α2,…,αn和V2的一组基β1,β2,…,βm,若σ是从线性空间V1到V2的线性映射,由于σ(αj)∈V2,因此
即
这组关系可以用矩阵形式表示为
今后把向量
(σ(α1),σ(α2),…,σ(αn))
简记作
σ(α1,α2,…,αn).
这样我们可以看到,线性映射σ即可由矩阵A=(aij)m×n完全描述.
反之,对于任意一个m×n阶矩阵A,都可以定义一个由n维线性空间V1到m维线性空间V2的线性映射,定义方法如下:
σ(α1,α2,…,αn)=(β1,β2,…,βm)A,
即
或者
称矩阵A为线性映射σ的矩阵.
这样,在给定线性空间V1和V2的基之后,我们就可以在V1到V2的线性映射σ与全体m×n阶矩阵之间,建立一个1—1对应关系.通常,我们把从线性空间V1到V2的全部线性映射组成的集合记作L(V1,V2).在进一步研究L(V1,V2)之前,我们先来看几个例子.
例5.1 在线性空间R3,R2中,记
ε1=(1,0,0)T,ε2=(0,1,0)T,ε3=(0,0,1)T,
η1=(1,0)T,η2=(0,1)T.
建立映射σ:R3→R2,σ((x,y,z)T)=(x,y)T,容易验证σ是一个线性映射.分别取R3的基ε1,ε2,ε3和R2的基η1,η2,则有
σ(ε1)=η1,σ(ε2)=η2,σ(ε3)=0.
线性映射σ的矩阵是
即
易见,σ是满射,因为对任意的(x,y)T∈R2,有σ((x,y,0)T)=(x,y)T;σ不是单射,因为尽管ε3≠0,但是仍然有σ(ε3)=σ(0)=0.并且很容易得到零向量的全部原像恰好为子空间{(0,0,z)T|z∈R}.(www.chuimin.cn)
例5.2 (续例5.1)建立映射τ:R2→R3,τ((x,y)T)=(y,x,0)T.容易验证τ是线性映射.显然,
τ(η1)=ε2,τ(η2)=ε1,
线性映射τ的矩阵是
τ是单射,因为从(x,y)T≠(x1,y1)T,易得τ((x,y)T)≠τ((x1,y1)T);但τ不是满射,因为,向量(0,0,1)T就没有原像.
例5.3 建立映射σ:M2(R)→M2(R), ,σ是线性映射.取M2(R)的一组基E11,E12,E21,E22,则
,σ是线性映射.取M2(R)的一组基E11,E12,E21,E22,则 ,其中i,j=1,2,因此,σ的矩阵是
,其中i,j=1,2,因此,σ的矩阵是
σ不是单射,因为尽管E12≠E21,但是σ(E12)=σ(E21);σ也不是满射,因为E12就没有原像.
若V1,V2都是数域F上的线性空间,可以在L(V1,V2)上定义两种运算,称为加法运算和数乘运算,分别记作σ+τ和kσ,这里σ,τ∈L(V1,V2),k∈F,它们的定义如下:
(σ+τ)α=σ(α)+τ(α),
(kσ)α=kσ(α).
其中α∈V1,k∈F.容易验证,这里定义的σ+τ和kσ都是从V1到V2的线性映射,即σ+τ,kσ∈L(V1,V2).
在选定V1,V2的基
α:α1,α2,…,αn,β:β1,β2,…,βm
之后,若线性映射σ,τ的矩阵分别为A,B,那么对向量 显然有
显然有
(σ+τ)γ=σ(γ)+τ(γ)
=σ(α)(k1,k2,…,kn)T+τ(α)(k1,k2,…,kn)T
=(β)A(k1,k2,…,kn)T+(β)B(k1,k2,…,kn)T
=(β)(A+B)(k1,k2,…,kn)T,
(kσ)γ=kσ(γ)
=kσ(α)(k1,k2,…,kn)T
=k(β)A(k1,k2,…,kn)T
=(β)(kA)(k1,k2,…,kn)T.
其中,
(α)=(α1,α2,…,αn),(β)=(β1,β2,…,βm).
因此,可以看到在选定线性空间的基之后,两个线性映射的和的矩阵等于各自的矩阵之和,与数的乘积的矩阵等于该数与其矩阵的乘积.这样就可以得到下面的定理:
定理5.1 设V1,V2都是数域F上的线性空间,维数分别为n,m,那么从V1到V2的全部线性映射组成的集合L(V1,V2)按照如上方式定义的加法运算和数乘运算构成数域F上的线性空间,并且有同构L(V1,V2)≅Mm×n(F).
此外,还可以定义两个线性映射之间的乘法运算,即映射的复合运算.设V1,V2,V3都是数域F上的有限维线性空间,线性映射σ1∈L(V1,V2),σ2∈L(V2,V3),那么按照映射复合的定义σ2°σ1就是一个从V1到V3的映射,容易验证,σ2°σ1是一个线性映射,通常记作σ2σ1.并且若σ1,σ2的矩阵分别为A,B,那么σ2σ1的矩阵恰好为BA.
习题
5.1.1.C0是习题3.1.2定义的线性空间.在C0上建立映射σ:C0→C0,满足条件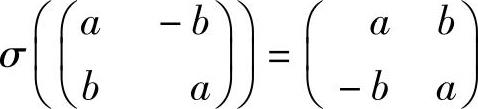 .
.
(1)证明:σ是线性映射;
(2)求出线性映射σ在基
之下的矩阵.
5.1.2. 设α1,α2,α3是R3的一组基,映射σ:R3→R3满足:
(1)证明:σ是线性映射;
(2)求出线性映射σ在基α1,α2,α3下的矩阵.
5.1.3. 在M2(R)中,映射γ:M2(R)→M2(R),满足
 .
.
(1)证明:τ是线性映射;
(2)求出线性映射τ在基E11,E12,E21,E22之下的矩阵.
5.1.4. 设映射σ:Rn[x]→R2n[x],满足σ(f(x))=f(x2),证明:σ是线性映射.
有关高等代数的文章

设σ是n维线性空间V1到m维线性空间V2的线性映射,即σ∈L.称集合{σ(α)|α∈V1}为线性映射σ的像空间,简称为像,记作Imσ;称集合{α|σ(α)=0}为线性映射σ的核空间,简称为核,记作kerσ.例5.4 在这个例子中,有Imσ=R2,kerσ=span(ε3).例5.5 在这个例子中,有Imτ=span,kerτ={0}.例5.6 在这个例子中,有Imσ=S,kerσ=T.命题5.3 若向量组α1,α2,…......
2023-11-22

,an,b是复数,则形如的方程称之为n元线性方程.由若干个n元线性方程组成的一组方程,称为线性方程组.能够使得线性方程组中所有方程同时成为等式的一组数值,称为方程组的一组解.下面我们初步探讨线性方程组的求解方法.例3.1若公鸡五文钱一只,母鸡三文钱一只,小鸡一文钱三只,现在用一百文钱买到一百只鸡,问:公鸡、母鸡、小鸡各买多少只?......
2023-11-22

,As都是方阵,那么形如的分块矩阵称为分块对角矩阵,简称分块对角阵,可以简单地记作diag(A1,A2,…,Es)有下面的三种分块初等矩阵:E=diag(E1,…......
2023-11-22

(1)若A为实对称矩阵,则①特征值均为实数,特征向量均为实向量.②不同特征值对应的特征向量正交.(即λ1≠λ2ξ1⊥ξ2(ξ1,ξ2)=0,建方程)③可用正交矩阵相似对角化.(即存在正交矩阵P,使P-1AP=PTAP=Λ)见例8.12至例8.15.(2)若A为正交矩阵,则ATA=EA-1=ATA由规范正交基组成AT是正交矩阵A-1是正交矩阵A*是正交矩阵-A是正交矩阵.(3)若A,B为同阶正交矩阵......
2023-11-21

定义4.1 设F是数域,V是一个非空集合,V中的元素具有两种运算,分别称为加法运算和数乘运算.所谓加法运算,就是一个对应法则,该法则使得集合V中任意两个元素α,β都对应于集合V中一个确定的元素γ,并称γ为元素α与β的和,记作γ=α+β.数乘运算是集合V中元素与数域F中的元素之间的运算法则,该法则使得集合V中任意一个元素α与数域F中任意一个数k,都对应于V中一个确定的元素δ,并称δ为k与α的数量乘积......
2023-11-22

,αm,βT线性无关.例5.16 已知齐次线性方程组A2×4x=0的基础解系为ξ1=[1,-1,3,2]T,ξ2=[2,1,1,-3]T,则A=________.应填,其中k1,l1,k2,l2 是不全为零的常数,且k1l2≠k2l1.由题设条件知,Aξ1=0,Aξ2=0,即两边转置,得作齐次线性方程组对系数矩阵作初等行变换,有取y2=0,y3=k,得,则解向量为取y2=l,y3=0,得,则解向量为其中k1,l1,k2,l2 是不全为零的常数,且k1l2≠k2l1.......
2023-11-21

,Ps,使得对所得矩阵再进行列的初等变换,变为即存在一些初等方阵Q1,Q2,…P2P1E=A-1.由于在矩阵的左边乘上一个初等方阵P,相当于对这个矩阵作一个与P相对应的初等行变换.上面两个等式表明,对A依次作P1,P2,…......
2023-11-22
相关推荐