，p-1的一个排列，利用定理1.1有a×2a×…......
2023-11-22
高等代数-直和定理：Rn=W1⊕W2
【摘要】：+Ws是直和，记作W1⊕W2⊕…⊕Ws.定理4.11 设W1，W2，…+dimWs..分别取每个子空间Wi的一组基αij，1≤j≤ri，其中dimWi=ri.由条件可以知道向量组αij，1≤i≤s，1≤j≤ri是和空间W的一组基，因此一定线性无关，由直和的定义知道W=W1+W2+…=xn}，证明：Rn=W1⊕W2.4.7.3. 在线性空间Rn中，取向量α1，α2，…
定义4.8 若V1和V2都是线性空间V的子空间，且V1∩V2={0}，则称和V1+V2为直和，并且记作V1⊕V2.
定理4.9 若V1和V2是n维线性空间V的子空间，则下列条件等价：
（1）V1+V2是直和；
（2）V1+V2中每个向量α都可唯一写成α=α1+α2的形式，其中α1∈V1，α2∈V2；
（3）V1+V2中零向量表示成两向量之和的方法是唯一的；
（4）dim（V1+V2）=dimV1+dimV2.
证明：（1）⇒（2），若α∈V1+V2，且
α=α1+α2=β1+β2，
其中
α1，β1∈V1，α2，β2∈V2.
则有等式
α1-β1=β2-α2.
从这个等式可见，
α1-β1∈V1，β2-α2∈V2.
由直和的定义知道V1∩V2={0}，因此，α1-β1=0，即α1=β1.同理有α2=β2.这表明在直和中任意一个向量的表示方法是唯一的.
（2）⇒（3），在（2）中取α=0即可.
（3）⇒（4），若dimV1∩V2>0，则存在0≠α∈V1∩V2，于是
0=0+0=α+（-α），
矛盾.因此，dimV1∩V2=0.由维数定理有结论成立.
（4）⇒（1），由维数定理有dimV1∩V2=0，此即V1∩V2={0}，也就是说，V1+V2是直和.
证毕.
定理4.10 若W是n维线性空间V的子空间，则存在V的子空间W′，使得V=W⊕W′.
证明：设dimW=r，取W的一组基α1，α2，…，αr，并把它扩充成V的一组基
α1，α2，…，αr，αr+1，…，αn.
取线性子空间
W′=span（αr+1，αr+2，…，αn），
则由定理4.9有dim（W+W′）=dimW+dimW′，所以，V=W⊕W′.证毕.
定义4.9 设W1，W2，…，Ws是线性空间V的子空间，W=W1+W2+…+Ws.如果每个向量α∈W表为W1，W2，…，Ws中向量和的方法是唯一的，则称和
W=W1+W2+…+Ws
是直和，记作
W1⊕W2⊕…⊕Ws.
定理4.11 设W1，W2，…，Ws是n维线性空间V的子空间，则下列条件等价：
（1）和W=W1+W2+…+Ws是直和；
（2）0表为W1，W2，…，Ws向量和的方法是唯一的；
（4）dimW=dimW1+dimW2+…+dimWs.
证明：（1）⇒（2）.由直和的定义这是显然的.
（2）⇒（3）.若向量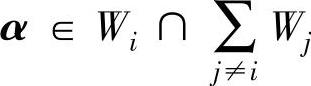
，则有α∈Wi且存在一组向量αj∈Wj，j≠i，使得(www.chuimin.cn)
记αi=-α，那么就有
由于零向量的表法是唯一的，因此
αi=0，1≤i≤s.
从中可以得到α=-αi=0，即证.
（3）⇒（4）.由条件显然有
因此
反复使用维数定理，可以得到
dimW=dim（W1+W2+…+Ws）
=dim（W1+W2+…+Ws-1）+dimWs
=…
=dimW1+dimW2+…+dimWs.
（4）⇒（1）.分别取每个子空间Wi的一组基αij，1≤j≤ri，其中dimWi=ri.由条件可以知道向量组
αij，1≤i≤s，1≤j≤ri
是和空间W的一组基，因此一定线性无关，由直和的定义知道W=W1+W2+…+Ws是直和.
证毕.
例4.30R2=span（ε1）⊕span（ε2），其中ε1=（1，0），ε2=（0，1）.
例4.31 在例4.29中，
R3=span（α1）⊕span（α2）⊕span（α3），
或者
R3=span（α1，α2）⊕span（α3）.
例4.32 在Rn-1[x]中，记Li=span（xi），0≤i≤n-1，则
Rn-1[x]=L0⊕L1⊕…⊕Ln-1.
例4.33 用Mn（R）表示实数域R上的所有n阶方阵的集合.对于矩阵的加法和数乘运算Mn（R）构成R上的线性空间.易证Eij，1≤i，j≤n，是Mn（R）的一组基，因此Mn（R）是一个n2维线性空间.
以S记Mn（R）中所有的对称矩阵的集合；T记Mn（R）中所有的反对称矩阵的集合.易于验证，S和T都是Mn（R）的线性子空间，且
因为每一个n阶方阵都可表示为一个对称矩阵与一个反对称矩阵之和的形式，所以Mn（R）=S⊕T.
习题
4.7.1.C0是习题4.1.2定义的线性空间.记
Ci=span（αi），i=1，2.证明：C0=C1⊕C2.
4.7.2. 在线性空间Rn中，记
W1={（x1，x2，…，xn）∈Rnx1+x2+…+xn=0}，
W2={（x1，x2，…，xn）∈Rnx1=x2=…=xn}，
证明：Rn=W1⊕W2.
4.7.3. 在线性空间Rn中，取向量α1，α2，…，αs，记
U=span（α1，α2，…，αs），
V={α∈RnαiαT=0，1≤i≤s}，
证明：V是Rn的一个子空间，且Rn=U⊕V.
有关高等代数的文章
- 详细阅读
-
行列式计算：高等代数-高等代数详细阅读
，xn）.解此递推关系可以得到例9.15 计算n阶行列式.解：将这个行列式的每一列都拆为两列，进而把行列式分成2n个行列式之和.当n>2时，它们中的每一个都有两列成比例.因此，行列式等于零.当n=1时，行列式等于a1+b1.当n=2时，行列式等于.例9.16 设四阶方阵，计算行列式|A|.解：由于所以|A|2=|A||AT|=|AAT|=4.再因为|A|中a4的系数为正，所以，|A|=2.例9.17 计算n阶循环行列式.解：这里我们记，以ζk=ζk，k=1，2，…......
2023-11-22
-
高等代数中集合与其运算-高等代数详细阅读
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2023-11-22
-
高等代数：线性空间的定义详细阅读
定义4.1 设F是数域，V是一个非空集合，V中的元素具有两种运算，分别称为加法运算和数乘运算.所谓加法运算，就是一个对应法则，该法则使得集合V中任意两个元素α，β都对应于集合V中一个确定的元素γ，并称γ为元素α与β的和，记作γ=α+β.数乘运算是集合V中元素与数域F中的元素之间的运算法则，该法则使得集合V中任意一个元素α与数域F中任意一个数k，都对应于V中一个确定的元素δ，并称δ为k与α的数量乘积......
2023-11-22
- 详细阅读
-
高等代数：计算特征值和特征向量详细阅读
，αr，并扩充为V的一组基α1，α2，…，n），求αTα的特征值.10.1.5. 证明方阵A可逆的充分必要条件是它的特征值均不是零.10.1.6. 若A可逆，证明：A-1的特征值是A的特征值的倒数.10.1.7. 证明：A2的全部特征值是A的特征值的平方.10.1.8. 证明：若λ1，λ2，…，f（λn）是矩阵f的全部特征值.10.1.9. 求出只与自身相似的所有方阵.10.1.10. 证明：A与AT相似.......
2023-11-22
-
高等数学基础：中值定理和函数单调性详细阅读
一、拉格朗日（Lagrange）中值定理定理1（拉格朗日中值定理）若函数f（x）满足条件：（1）在闭区间[a，b]上连续；（2）在开区间（a，b）内可导；则至少存在一点ξ∈（a，b），使得或图3.1拉格朗日中值定理的几何意义：如果在闭区间[a，b]上连续的一条曲线弧y=f（x）除端点外处处具有不垂直于x轴的切线，则曲线上至少存在一点C，使得曲线在点C处的切线平行于连接曲线两端点的弦AB.显然，......
2023-11-20
-
高等代数：f和g的最大公因式ars详细阅读
==ars，其中ars是f和g的最大公因式，且是由它们唯一确定的首一多项式.上述这组等式通过简单的移项，我们可以得到下面一组等式把rs-1，rs-2，…......
2023-11-22
相关推荐