高等代数教你如何进行坐标变换

2023-11-22 理论教育版权反馈

【摘要】：由例4.22可以看到，在线性空间V中，同一向量在不同的基之下的坐标不一定相同.本节研究同一向量在不同基之下的坐标之间的关系，由此得到一般的线性空间中的坐标变换公式.设在n维线性空间V中任意选定两组基α与β，分别为α：α1，α2，…

由例4.22可以看到，在线性空间V中，同一向量在不同的基之下的坐标不一定相同.本节研究同一向量在不同基之下的坐标之间的关系，由此得到一般的线性空间中的坐标变换公式.

设在n维线性空间V中任意选定两组基α与β，分别为

α：α₁，α₂，…，α_n，

β：β₁，β₂，…，β_n，

V中向量γ在这两组基之下的坐标分别为

（x₁，x₂，…，x_n）^T，（y₁，y₂，…，y_n）^T.

由于α₁，α₂，…，α_n是一组基，因此有β_i（i=1，2，…，n）可由α₁，α₂，…，α_n线性表出，即

β_j=a_1jα₁+a_2jα₂+…+a_njα_n，j=1，2，…，n.

这组关系可以很容易地写成矩阵形式就是

记矩阵A=（a_ij）_n×n，显然矩阵A是唯一确定的，称为由基α₁，α₂，…，α_n到基β₁，β₂，…，β_n的过渡矩阵.

同样，存在矩阵B=（b_ij）_n×n，使得

（α₁，α₂，…，α_n）=（β₁，β₂，…，β_n）B.

此时，有

（β₁，β₂，…，β_n）=[（β₁，β₂，…，β_n）B]A=（β₁，β₂，…，β_n）（BA），

即

（β₁，β₂，…，β_n）（E_n-BA）=（0，0，…，0）.

由于β₁，β₂，…，β_n是一组基，可见，AB=E_n.同理，有BA=E_n.由此可以看到，过渡矩阵一定是可逆矩阵，且从基α到基β的过渡矩阵与从基β到基α的过渡矩阵互为逆矩阵.

对于向量γ来说，一方面有

由于坐标是唯一确定的，因此

或

公式（4.2）与公式（4.3）称为坐标变换公式.

例4.23 在平面R²上选定一组向量

α₁=（1，1），α₂=（1，-1）

作为基，则向量α=（-2，4）的坐标是.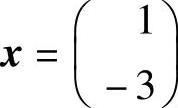

另选一组向量β₁=（1，3），β₂=（-3，1）作为基.由于

β₁=2α₁-α₂，β₂=-α₁-2α₂，

写成矩阵形式是

由基α₁，α₂到β₁，β₂的过渡矩阵

其逆矩阵

向量α在基β₁，β₂下的坐标是

例4.24 在R_n-1[x]中，选定一组基(www.chuimin.cn)

1，x，…，x^n-1，

依次记作

α₁，α₂，…，α_n.

再选取一组基

1，x-1，…，（x-1）^n-1，

依次记作

β₁，β₂，…，β_n.

则有

因此，基α₁，α₂，…，α_n到基β₁，β₂，…，β_n的过渡矩阵A=（a_ij）_n×n，其中

同样，由于

因此，基β₁，β₂，…，β_n到基α₁，α₂，…，α_n的过渡矩阵B=（b_ij）_n×n，其中

并且AB=BA=E.

多项式f（x）=a_n-1x^n-1+…+a₁x+a₀在基1，x，…，x^n-1之下的坐标是

那么，在基1，x-1，…，（x-1）n-1之下的坐标是Y=BX，其中第k个分量是

由于AB=E，因此我们有组合恒等式

其中δ_ij是Kronecker符号，1≤i≤j≤n.

习题

4.4.1. 在线性空间R³中，

（1）证明：α₁=（1，0，0），α₂=（1，1，0），α₃=（1，1，1）也是一组基；

（2）求出从基e₁，e₂，e₃到基α₁，α₂，α₃的过渡矩阵；

（3）求出从基α₁，α₂，α₃到基e₁，e₂，e₃的过渡矩阵.

4.4.2.C⁰是习题4.1.2定义的线性空间.

（1）证明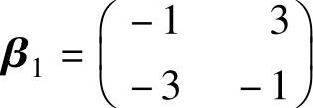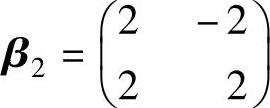：，也是C⁰的一组基；

（2）求出从基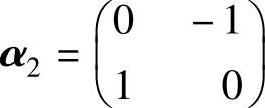，到基β₁，β₂的过渡矩阵；

（3）求出C⁰中的向量在上述两组基下的坐标间的关系；

（4）若矩阵γ在基β₁，β₂下的坐标是，求γ在基α₁，α₂下的坐标.

4.4.3. 在线性空间R_n[x]中，

（1）证明：β_i=1+x+…+x^i-1（1≤i≤n）是R_n[x]的一组基；

（2）求出从基1，x，…，x^n-1到上述这组基下的过渡矩阵；

（3）求出多项式f（x）=a_n-1x^n-1+…+a₁x+a₀在β_i（1≤i≤n）之下的坐标.

高等代数教你如何进行坐标变换

相关推荐