首页理论教育高等代数中αn的坐标及向量组的维数和矩阵坐标

高等代数中αn的坐标及向量组的维数和矩阵坐标

2023-11-22 理论教育版权反馈

【摘要】：，αn之下的坐标.向量α可以按以下形式写成显然，当基取定之后，每一个向量的坐标都是唯一确定的.反之，对于任意一个有序数组（k1，k2，…，（x-1）n-1，则由微积分中的Taylor公式有因此，f在这组基下的坐标为习题4.3.1.C0是习题4.1.2定义的线性空间.证明：，是线性空间C0的一组基；计算dimC0；求出矩阵在上述这组基下的坐标.4.3.2.Mn作为R上的线性空间的维数是多少？，αn是V的一组基.4.3.5. 设V是n维线性空间，向量组α1，α2，…

维数是经常遇到的一个数学概念.例如，通常所说的二维平面和三维空间等.本节将解释维数这个概念的真实意义.

定义4.5 如果在线性空间V中，存在n个线性无关的向量α₁，α₂，…，α_n，使得V中的任意一个向量都可由这组向量线性表示，则称V是一个n维线性空间.向量组α₁，α₂，…，α_n称为线性空间V的一组基，n称为线性空间V的维数，记作dimV=n.

维数有限的线性空间，称为有限维线性空间.本课程只重点讨论有限维线性空间.

例4.17 全体n元有序数组组成的集合

Rⁿ={（x₁，x₂，…，x_n）|x_i∈R，i=1，2，…，n}

按向量的加法和数乘，构成一个n维线性空间.容易验证由n个向量组成的向量组

e₁=（1，0，…，0），e₂=（0，1，…，0），…，e_n=（0，0，…，1）

是Rⁿ的一组基.

例4.18 次数低于n的全体实系数多项式集合

R_n-1[x]={a₀+a₁x+…+a_kx^k|k<n，a₀，a₁，…，a_k∈R}

按照普通的多项式运算构成R上的n维线性空间，易证多项式组

1，x，x²，…，x^n-1

是它的一组基.

例4.19 全体实系数多项式集合

R[x]={a₀+a₁x+…+a_nxⁿ|n≥0，a₀，a₁，…，a_n∈R}

构成一个线性空间.但是，任意有限多个多项式不可能成为该线性空间的一组基.这样的线性空间称为无限维的.

例4.20 只含一个零向量的集合V={0}是一个线性空间，这个空间称为零空间，零空间的维数是零.

例4.21n维线性空间中的线性无关向量组最多只含有n个向量.换句话说，在一个n维线性空间中，任意n+1个向量一定是线性相关的.

若V是数域F上的n维线性空间，α₁，α₂，…，α_n是V的一组基.对于V中任意一个向量α，由基的定义可以知道，α可以写成α₁，α₂，…，α_n的线性组合

的形式，且组合系数k₁，k₂，…，k_n∈F是唯一确定的.以一个n元有序数组

表示这组系数，称为向量α在基α₁，α₂，…，α_n之下的坐标.向量α可以按以下形式写成

显然，当基取定之后，每一个向量的坐标都是唯一确定的.

反之，对于任意一个有序数组（k₁，k₂，…，k_n）^T，以它为坐标的向量

也是唯一确定的.这样在取定基之后，可以用一个n元有序数组来表示V中的向量，即一个向量和该向量在这组基下的坐标是等同的.

在引入坐标之后，线性空间中向量的运算可以完全由坐标表出.在n维线性空间V中，取定一组基α₁，α₂，…，α_n，V中向量α与β的坐标分别是(www.chuimin.cn)

即

则有

也就是说，α+β的坐标就是α的坐标与β的坐标之和；α的k倍的坐标就是α的坐标的k倍.由此可以看到，n维线性空间V和Rⁿ具有相同的结构.

例4.22 在线性空间R_n-1[x]中，如果给定基为

1，x，…，x^n-1，

则f（x）=a_n-1x^n-1+…+a₁x+a₀的坐标为

如果给定一组基为

1，x-1，…，（x-1）^n-1，

则由微积分中的Taylor公式有

因此，f（x）在这组基下的坐标为

习题

4.3.1.C⁰是习题4.1.2定义的线性空间.

（1）证明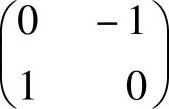：，是线性空间C⁰的一组基；

（2）计算dimC⁰；

（3）求出矩阵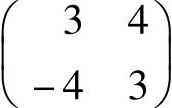在上述这组基下的坐标.

4.3.2.M_n（R）作为R上的线性空间的维数是多少？为什么？

4.3.3. 给出线性空间M₂（R）的一组基，并找到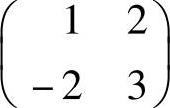在你给出的基下的坐标.

4.3.4. 若线性空间V中的n个向量α₁，α₂，…，α_n满足下述条件：

（1）V中任意向量都是α₁，α₂，…，α_n的线性组合；

（2）V中有一个向量α₀，它写成α₁，α₂，…，α_n的线性组合的方式是唯一的.证明：α₁，α₂，…，α_n是V的一组基.

4.3.5. 设V是n维线性空间，向量组α₁，α₂，…，α_n和β₁，β₂，…，β_n是V的两组基.证明：存在1，2，…，n的一个排列i₁，i₂，…，i_n，使得

α₁，…，α_j-1，β_ij，α_j+1，…，α_n

都是V的基，1≤j≤n.