高等代数：矩阵秩原理及应用

2023-11-22 理论教育版权反馈

【摘要】：解：是.由Am×r是列满秩矩阵，则存在行满秩矩阵Pr×m，使得PA=Er.在等式Am×rBr×n=Om×n两端左边乘P，则有Pr×m=Pr×mOm×n=Or×n及Br×n=ErBr×n=Br×n，比较两式可知B=O.是.显然有A（B-C）=O，利用的结论即得B-C=O.习题3.6.1. 如果AB，BA都是有意义的，那么它们是否具有相等的秩？，As都是n阶方阵，证明：并且等号可以取到.3.6.

矩阵的秩是矩阵在相抵下的一个重要的不变量，本节着重讨论这个概念.首先，有如下定理：

定理3.10 设A是m×n阶矩阵，那么有不等式

rankA_m×n≤min{m，n}.

证明：从矩阵的秩的定义3.12，可以看出

rankA_m×n≤m，

rankA_m×n≤n，

两个不等式合在一起就是

rankA_m×n≤min{m，n}.

证毕.

定理3.11m×n阶矩阵A的秩等于r，即rankA_m×n=r的充分必要条件是存在可逆方阵P_m，Q_n，使得

证明：由定理3.4与定理3.5，以及秩的定义3.12立即就可以得到这个结果.证毕.

推论3.1 一个矩阵与它的转置矩阵有相同的秩，即rankA=rankA^T.

证明：设矩阵A的秩为r，那么由定理3.11，一定可以找到可逆矩阵P，Q使得

将式（3.29）两端的矩阵转置得到

由于E^T_r=E_r，因此转置矩阵A^T的秩也为r，即

rankA=rankA^T.

证毕.

定理3.12 初等变换不改变矩阵的秩，或者说秩是矩阵在初等变换下的不变量.

证明：只要注意到相抵的矩阵有相同的标准形即可.证毕.

推论3.2 设A是m×n阶矩阵，P，Q分别是m阶、n阶可逆方阵，则有

rankA=rankPA=rankAQ=rankPAQ.

简单地说就是，一个矩阵与一个可逆矩阵相乘秩不变.

证明：由于每一个可逆矩阵都是一些初等矩阵的乘积，而矩阵与一个初等矩阵相乘相当于进行一次初等变换，因此秩是不会改变的.证毕.

对于可逆方阵，我们有：

定理3.13n阶方阵A可逆的充分必要条件是rankA=n.

证明：必要性，若A可逆，则存在初等矩阵P₁，P₂，…，P_s，使得

P₁P₂…P_sA=E.

故此，A的相抵标准形为E，即得rankA=n.

充分性，若rankA=n，则A的相抵标准形为单位矩阵E.因此，由定理3.11知道存在可逆方阵P，Q，使得

A=PEQ=PQ，

因此A可逆.证毕.

引理3.1 设A，B分别是m×n，m×k阶矩阵，则

rankA≤rank（A，B）≤rankA+k.

证明：对k=1证明即可.设rankA=r，则存在可逆矩阵P，Q使得

这时有

易得

rankA≤rank（A，B）≤rankA+1.

利用这个不等式，对引理中的k用归纳法可以证明一般结论.证毕.

定理3.14 设矩阵A与B是同型的，则它们的和的秩不超过各自的秩的和，即有不等式

rank（A+B）≤rankA+rankB.

证明：设rankA=r，rankB=s，则存在可逆方阵P₁，Q₁，P₂，Q₂，使得

则有

所以，

又因为

而矩阵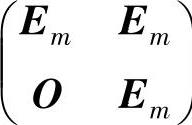与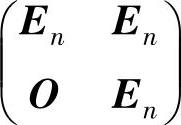都可逆，所以，

证毕.

定理3.15 设A，B分别是m×n，n×k阶矩阵，则有下面的不等式成立：

rankA_m×n+rankB_n×k-n≤rankA_m×nB_n×k≤min{rankA_m×n，rankB_n×k}.

证明：首先证明定理的右半部分.设rankB=s，则存在可逆矩阵P₁，Q₁，使得

那么，

其中，E_ij是一个n×k阶矩阵，它的第i行第j列元素是1，其余元素都是0，右边的不等式成立.

下面证明左半部分.再设rankA=r，存在可逆矩阵P，Q使得

则

由推论3.2有

记T=QP₁=（t_ij）n，则T可逆.把T分块为

其中T₁是s×t矩阵，则有

于是由引理3.1，有

证毕.

例3.12 若rankA_m×n=r，则存在m×r及r×n阶矩阵G，H，使得A=GH，且rankG=rankH=r.

证明：由定理3.11，存在m阶与n阶可逆方阵P，Q，使得

取

则A=GH，且rankG=rankH=r.证毕.

例3.13 若n阶方阵A满足条件A²=A（称为幂等矩阵），则

rankA+rank（E-A）=n.

证明：由条件有A（E-A）=O.由定理3.14知

rankA+rank（E-A）≥rank（A+E-A）=n.

由定理3.15知(www.chuimin.cn)

0=rankA（E-A）≥rankA+rank（E-A）-n.

因此，有

rankA+rank（E-A）=n.

证毕.

例3.14 若方阵A是n阶幂等矩阵，则存在可逆矩阵P，使得

这里，r=rankA.

证明：由于rankA=r，则存在n阶可逆矩阵P，Q使得

由于A是幂等矩阵，因此A²=A，即

由于P，Q可逆，式（3.31）即

引入记号

这时S可逆，且S₁₁是r阶方阵，式（3.32）成为

即

得到S₁₁=E_r.在式（3.32）右端同时乘QP，得

以矩阵S=QP代入左边得到

即

在式（3.33）左端乘P，右端乘P^-1，得到

即

最后，令矩阵

则有

而

将式（3.34）中的PT看作P，正是要证明的结论.证毕.

例3.15 若方阵A是n阶幂等矩阵，则trA=rankA.

证明：由例3.14有

定义3.14 设A是m×n阶矩阵，若rankA=m，则称矩阵A是行满秩矩阵；若rankA=n，则称矩阵A是列满秩矩阵.

例3.16 若列满秩矩阵rankH_m×r=r，则存在行满秩矩阵G_r×m，使得GH=E_r.

证明一：首先，由于rankH_m×r=r，因此存在m阶、r阶可逆矩阵P，Q使得

即

容易看到矩阵

是一个可逆矩阵.因此，存在m阶可逆矩阵P₀，使得

将矩阵P₀分块，前r行记为G，后m-r行记为G₀，则有

比较得GH=E_r.

证明二：由于rankH_m×r=r，存在m阶、r阶可逆矩阵P，Q使得

取

G=Q^-1（E_rO）P^-1，

则GH=E_r.证毕.

例3.17 设A是列满秩矩阵，

（1）若AB=O，问B是否一定为零矩阵？

（2）若AB=AC，是否一定有B=C？

解：（1）是.由A_m×r是列满秩矩阵，则存在行满秩矩阵P_r×m，使得PA=E_r.在等式

A_m×rB_r×n=O_m×n

两端左边乘P，则有

P_r×m（A_m×rB_r×n）=P_r×mO_m×n=O_r×n

及

（P_r×mA_m×r）B_r×n=E_rB_r×n=B_r×n，

比较两式可知B=O.

（2）是.显然有A（B-C）=O，利用（1）的结论即得B-C=O.

习题

3.6.1. 如果AB，BA都是有意义的，那么它们是否具有相等的秩？为什么？

3.6.2. 设A，B都是方阵，证明：

3.6.3. 设A是可逆矩阵，则

3.6.4. （Frobenius不等式）

rank（ABC）+rankB≥rank（AB）+rank（BC）.

3.6.5. 设A₁，A₂，…，A_s都是n阶方阵，证明：

并且等号可以取到.

3.6.6. 证明：m×n阶矩阵A的秩为1的充分必要条件是，存在非零的m维列向量α和非零的n维行向量β，使得A=αβ.

3.6.7.n阶方阵A是幂等阵的充分必要条件是

rankA+rank（E-A）=n.

3.6.8.n阶方阵A是对合阵的充分必要条件是

rank（E+A）+rank（E-A）=n.

3.6.9. 若A是对合阵且rank（E+A）=r，则存在可逆矩阵P，使得

P^-1AP=diag（E_r，-E_n-r）.

3.6.10. 设n阶方阵A的秩是r，且A³=A.求证：存在可逆矩阵P，使得

P^-1AP=diag（E_s，-E_r-s，O），

这里，0≤s≤r.

3.6.11. 设A是n阶方阵，且rankA=r，则存在可逆矩阵P，使得

其中B是行满秩矩阵.

高等代数：矩阵秩原理及应用

相关推荐