首页理论教育高等代数：线性方程组与矩阵

高等代数：线性方程组与矩阵

2023-11-22 理论教育版权反馈

【摘要】：，an，b是复数，则形如的方程称之为n元线性方程.由若干个n元线性方程组成的一组方程，称为线性方程组.能够使得线性方程组中所有方程同时成为等式的一组数值，称为方程组的一组解.下面我们初步探讨线性方程组的求解方法.例3.1若公鸡五文钱一只，母鸡三文钱一只，小鸡一文钱三只，现在用一百文钱买到一百只鸡，问：公鸡、母鸡、小鸡各买多少只？

在平面直角坐标系中，直线的方程是一个一次方程，如2x+3y=1.像这样变量次数为1的方程，称之为线性方程.一般来说，若x1，x2，…，xn是一组变量，a₁，a₂，…，a_n，b是复数，则形如

的方程称之为n元线性方程.由若干个n元线性方程组成的一组方程，称为线性方程组.能够使得线性方程组中所有方程同时成为等式的一组数值，称为方程组的一组解.

下面我们初步探讨线性方程组的求解方法.

例3.1（百钱买百鸡问题）若公鸡五文钱一只，母鸡三文钱一只，小鸡一文钱三只，现在用一百文钱买到一百只鸡，问：公鸡、母鸡、小鸡各买多少只？

解：如果我们分别以x，y，z表示买到的公鸡、母鸡、小鸡的只数，则依照题意，易见

x+y+z=100 （3.1）

及

由此，我们得到两个三元一次方程，而问题是要寻求同时满足这两个方程的数x，y，z.当然此处的变量x，y，z必须是正整数，由方程（3.1）和方程（3.2）组成的一组方程称之为方程组，记为

验算易得x=12，y=4，z=84是问题的一个解答，像这样使得方程组中所有方程同时成立的一组数称之为这个方程组的解.

例3.2 寻找一条抛物线y=ax²+bx+c，使得（1，0），（2，0），（3，2）三点在其上.

解：由平面解析几何的知识可知，若给出的三点在抛物线上，即要求

我们要找出合适的a，b，c使这三个线性方程同时成立，也就是需要求出以下方程组的解：

由式（3.3）的第一式可知a=-b-c，将之代入第二、三两式分别得出

由式（3.4）的第一式得出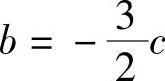，代入式（3.4）的第二式得出c=2，依次代回可得出b=-3，a=1，即解得抛物线应是y=x²-3x+2.

对于一般的n元线性方程组，也可以通过这种逐步代入，依次消去变元的方法，最终求得方程组的解.这种通过消元，最终获得方程组的解的方法，称为高斯（Gauss）消元法.我们将在第7章中进一步深入讨论用消元法解方程组.这里来初步分析一下这种解方程组的方法的实质是什么.

分析上面的例3.2中使用高斯消元法求解的过程可以看到，最初需要求解的方程组是(www.chuimin.cn)

经过第一次消元，消去变量a，得到方程组

从此方程组中求得b，c，进而求出a的值.实际上，这相当于在求解一个如下的和原方程组（3.5）本质上相同的方程组

进一步消去b，相当于去求解一个和方程组（3.7）本质上相同的方程组

代回的过程相当简单，相当于依次求解方程组

和

这就是用消元法解方程组的实际过程.

另一方面，类似于多项式运算的分离系数法，我们易于看到变量的名称的选取是无关紧要的，因此，方程组的解取决于变量之间的关系、变量的系数，而与名称无关.这样我们从方程组（3.5）中除去加号、等号、变量名称，即可得到如下的一张数表：

此表揭示了方程组的最本质的内容，像这样的一个数表，我们称之为矩阵，并以下列记号表示：

而解方程组的过程又可表示为从矩阵（3.11）出发依次得到如下一系列矩阵（式（3.12）～式（3.15））.

直接对比以上过程，我们有下面的表格.

可见，矩阵对于方程组来说，是一种重要而简洁的记录方式.

一般地，由m×n个数a_ij（1≤i≤m，1≤j≤n）组成的如下数表：

称为m行n列的矩阵，或m×n阶矩阵，记作（a_ij）m×n.如果不需要强调矩阵的阶数，那么也可以简单地记作（aij）.一般地，我们使用大写字母A，B，C，…表示矩阵.矩阵中的数称为矩阵的元素.

有时，我们把1×n矩阵称为n维行向量，而把n×1矩阵称为n维列向量.