图2-7展示了本章所采取的逐类学习纹理基元,最终构建纹理基元字典的实现过程。按照上述步骤的方法,依次从每个类别的训练样本中学习Nt个纹理基元,然后把从所有类别学习到的纹理基元进行合并,将其作为纹理基元字典。最后,需要对纹理基元字典中非常相似的纹理基元进行删除。因此,必须删除纹理基元字典中冗余的纹理基元。......
2023-06-29
从本节开始,我们讨论多元多项式的性质与应用.
设F是一个数域,x1,x2,…,xn是n个独立的未定元,称形如
的表达式为关于未定元x1,x2,…,xn的一个n元单项式.si称为单项式中不定元xi的次数,i=1,2,…,n.当a≠0时,称
s1+s2+…+sn
为这个单项式的次数,也记作deg;a依然称为这个单项式的系数.当a=0时,这个单项式的次数规定为-∞.
除系数以外完全相同的非零单项式称为同类项.可以很容易地定义同类项之间的加法、减法与乘法运算如下:
也就是说,只有同类项之间才可以进行加减运算,运算规则为将系数进行相应的加减;乘法的运算规则为系数相乘,相同不定元的次数相加.例如,
3x41x32x4+5x41x32x4=8x41x32x4,
2x1x32x23·(-2)x41x52x3=-4x51x28x33,
12x21x22x23·7x31x32x43=84x51x52x23x43,
等.单项式的加减运算也称为合并同类项.
由有限多个单项式形式相加得到的表达式称为多项式,即形如
的表达式称为n元多项式.它所含的单项式的最高次数称为这个多项式的次数.多元多项式的次数仍然记作deg.例如,多项式
-2x31x22x4+5x72+13x1x2x53x24-8x41x53-x4,
x31+x21x2+x1x22+x23,
xn+yn
分别是9次、3次与n次多项式.某一数域F上关于文字x1,x2,…,xn的全部多项式的集合记作F[x1,x2,…,xn],称为多元多项式环.
显然,每一个单项式也都是一个多项式.我们可以利用加法与乘法满足的运算律来定义多元多项式的加法与乘法运算.若f,g,h是多元多项式,可以在它们之间定义加法与乘法运算,使得这两种运算满足条件:
(1)加法交换律 f+g=g+f;
(2)加法结合律 (f+g)+h=f+(g+h);
(3)乘法交换律 fg=gf;
(4)乘法结合律 (fg)h=f(gh);
(5)分配律 (f+g)h=fh+gh.
例如,我们有
(2x21x3-3x2)(3x2x43+x1x3)=6x21x2x53+2x31x23-9x22x43-3x1x2x3,
(x1+x2+x3)(x1-x2+x3)=x21-x22+x23+2x1x3,
等.
在一元多项式理论中,多项式的带余除法运算有着十分重要的地位,其研究方法主要依赖于多项式可以按照次数从高到低进行排序.但对于多元多项式来说,按照次数排序是不合理的,如多项式x4+x2y2+y4该如何进行排序呢?为了解决这个问题,我们可以引入字典排序法.
设有n个未定元x1,x2,…,xn,固定它们的顺序为下标的自然顺序.关于这n个未定元的两个单项式 与
与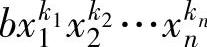 ,ab≠0,它们的未定元的次数构成两个有序数组(l1,l2,…,ln)与(k1,k2,…,kn),如果这两个有序数组对某个下标i满足条件
,ab≠0,它们的未定元的次数构成两个有序数组(l1,l2,…,ln)与(k1,k2,…,kn),如果这两个有序数组对某个下标i满足条件
l1=k1,…,li-1=ki-1,li>ki,
那么就称单项式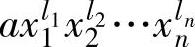 是先于单项式
是先于单项式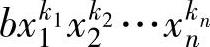 的,或者单项式
的,或者单项式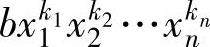 是后于单项式
是后于单项式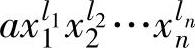 的,记作
的,记作
(l1,l2,…,ln)≺(k1,k2,…,kn)或者(k1,k2,…,kn)≻(l1,l2,…,ln).
在一个多项式中,按照出现的单项式之间的先于关系将多项式的项进行排列,即若f先于g,那么f总是更靠前.注意这里的顺序与单项式的次数无关.这种排列多元多项式的方法称为字典排序法.例如,
x31x2x23-3x31x3+4x1x2-9x72x43-x42x73,
x41-2x21x22-2x21x23+x42-2x22x23+x43,
等.
引理2.5 若f1,f2,g1,g2都是非零单项式,且满足条件f1先于f2,g1先于g2,那么一定有f1g1先于f2g2.
证明:设单项式
这时一定有关系
(l1,l2,…,ln)≺(l1′,l2′,…,ln′),(k1,k2,…,kn)≺(k1′,k2′,…,kn′).
这时,必然有自然数i,j使得
l1=l1′,…,li-1=li′-1,li>li′,
k1=k1′,…,kj-1=kj′-1,kj>kj′.
若i=j,则有
l1+k1=l1′+k1′,…,li-1+ki-1=li′-1+ki′-1,li+ki>li′+ki′,
即(www.chuimin.cn)
(l1+k1,l2+k2,…,ln+kn)≺(l1′+k1′,l2′+k2′,…,ln′+kn′).
也就是说,单项式f1g1是先于单项式f2g2的.若i<j,则有li>li′,ki=ki′,此时必然有
l1+k1=l1′+k1′,…,li-1+ki-1=li-1′+ki-1′,li+ki>li′+ki′,
即
(l1+k1,l2+k2,…,ln+kn)≺(l1′+k1′,l2′+k2′,…,ln′+kn′).
因此,单项式f1g1是先于单项式f2g2的.同理可证i>j的情况.证毕.
定理2.17 按照字典排序法,两个多元多项式的乘积的首项正好是它们各自的首项的乘积.
由引理2.5立刻可以得到这个结论.
推论2.11 两个非零多项式的乘积一定是非零多项式,或者说,两个多项式的乘积等于零多项式的话,那么它们中至少有一个是零多项式.
对于多元多项式还有一个概念叫作齐次多项式.
定义2.11 若一个n元多项式中,每一项的次数都是m,那么就称这个多项式为n元m次齐次多项式,简称m次齐次多项式.
例如,
x21-2x22,
x3+y3+z3-3xyz,
x1x2x45+3x72+x2x64+x33x44
分别是二次、三次与七次齐次多项式.
若f是一个m次多项式,那么可以把它的次数相同的部分分开,次数为i的部分记作fi,那么就有
f=fm+fm-1+…+f1+f0.
也就是说,有如下引理:
引理2.6 任何一个多元多项式都可以写成一些齐次多项式的和的形式.
定理2.18 若f,g都是n元多项式,那么
deg(f+g)≤max{degf,degg} (2.45)
deg(fg)=degf·degg. (2.46)
证明:若f,g都是n元多项式,次数分别为m,m′,记
f=fm+…+f1+f0,g=gm′+…+g1+g0,
其中f0,f1,…,fm是多项式f的齐次部分,g0,g1,…,gm′是多项式g的齐次部分.若m<m′,那么
deg(f+g)=m′=degg=max{degf,degg}.
若m=m′,那么在fm+gm=0时有
deg(f+g)<m=degf=degg=max{degf,degg}.
在fm+gm≠0时有
deg(f+g)=m=degf=degg=max{degf,degg}.
综合就有
deg(f+g)≤max{degf,degg}.
在乘法的情况,fm的每一项都是m次的单项式,gm′的每一项都是m′次的单项式,由乘法规则可以看到fmgm′的每一项都是m+m′次单项式.另外,按照字典排序法,fm的首项与gm′的乘积正好是fmgm′的首项,因此,
deg(fmgm′)=degfm+deggm′.
再由加法的次数关系可以看到
deg(fg)=degf·degg.
对于多元多项式也可以定义整除的概念:
定义2.12 若f,g是数域F上的两个多元多项式,如果存在另一个多元多项式h使得f=gh,那么就说g是f的一个因式,或者说,g整除f.
习题
2.8.1. 设f(x1,x2,…,xn)∈F[x1,x2,…,xn].证明:f是m次齐次多项式的充要条件是
f(tx1,tx2,…,txn)=tmf(x1,x2,…,xn).
2.8.2. 如果m次多项式f(x1,x2,…,xn)可以分解为两个非零多项式g,h的乘积,即f=gh,则称多项式f是可约的.求证:任意一个多项式f(x1,x2,…,xn)或为不可约的,或为有限多个不可约多项式的乘积.
2.8.3. 求证:形如f(x)+y的二元多项式是不可约多项式.
2.8.4. 求证:若(f(x),g(x))=1,则二元多项式f(x)+yg(x)是不可约多项式.
有关高等代数的文章

图2-7展示了本章所采取的逐类学习纹理基元,最终构建纹理基元字典的实现过程。按照上述步骤的方法,依次从每个类别的训练样本中学习Nt个纹理基元,然后把从所有类别学习到的纹理基元进行合并,将其作为纹理基元字典。最后,需要对纹理基元字典中非常相似的纹理基元进行删除。因此,必须删除纹理基元字典中冗余的纹理基元。......
2023-06-29

定理10.2 若f(λ)是n阶方阵A的特征多项式,则f=0.证明:设B(λ)是n阶方阵λE-A的伴随矩阵,则利用伴随矩阵的性质有B(λ)=f(λ)E.由于B(λ)的元素都是方阵λE-A的n-1阶子式,因此,都是λ的次数最多是n-1次多项式.这样,B(λ)可以写成如下形式:B(λ)=λn-1B0+λn-2B1+…+an-1A+anE=O.证毕.推论10.1 设线性变换σ的特征多项式是f(λ),那么f(σ)=0.注意 这里f(σ)是一个线性变换.定理10.3 设n阶方阵A的特征多项式是λn+a1λn-1+…......
2023-11-22

也可以用图16-6的形象方法解读,将变量B反向延长,物种1和物种分别投影于其上,可以很清楚地看出物种2的投影与B同向,代表正相关;同理,物种1为负相关。图16-12基于RDA双序图上分析物种沿海拔梯度分布情况2.基于单峰模型排序图的解读。......
2023-11-17

加德纳把开发学生的多元智能作为学校教育的宗旨。因此,加德纳的多元理论也为我们全面推进素质教育提供了新的理论依据。多元智能理论关键的一点是:大多数人的各项智能都可能发展到一个很高的水平。⑤自我省思智能教学法。多元智能理论为我们提供了一种学生个人主体发展的模式,它帮助教育工作者改进教学方法,拓宽活动范围,使学生一些被忽视的智能得到发展,未发展或关闭的智能得以激发,已发展的智能得以完善。......
2023-10-31

+a1α+a0∈F称为多项式f在x=α处的值,记作f(α)=anαn+an-1αn-1+…,αn+1是n次多项式f的不同的根.显然,x-αi一定两两互素,因此,f=q…,考虑多项式两端的次数可以看到只有f=0.证毕.推论2.6 若两个n次多项式在n+1个不同的点取值相同,则它们必相等.证明:设f,g是数域F上的n次多项式,且在n+1个不同的点αi,i=1,2,…......
2023-11-22

,xn 是从一元总体中抽取的.一元数据的数字特征主要有:均值,方差s2=,标准差s=,等等.对于多元数据,除分析各分量的取值特征外,还要分析各分量之间的相关关系.由于多元统计分析中的符号多而杂,因此需要说明:在一元统计学中一般用大写和小写字母分别来区分随机变量及其观测值,在本书后面的章节里,由于其他复杂的符号,我们可能不再遵守此约定,请读者注意一个符号在每一章中的意义.......
2023-11-18
相关推荐