一个有理系数多项式anxn+…，bn的最大公因数是1.这样的工作总是能够完成的，如我们可以先形式上通分，然后把分母以及分子系数的公因数同时提出.由此可见，有理系数多项式anxn+…+b1x+b0的因式分解问题.以下我们只讨论整系数多项式的因式分解问题.首先我们引入本原多项式的概念.定义2.10 若整系数非零多项式f=anxn+…......
2023-11-22
复系数与实系数多项式-《高等代数》简介
【摘要】：前面的讨论已经知道，数域F上的多项式在F内一定可以分解为一些不可约多项式的乘积.但是，一个多项式在不同数域内的分解情况是不一样的.例如，多项式x4-4，在有理数域Q内可以分解为（x2-2）（x2+2）；在实数域R内可以分解为在复数域C内可以分解为在一些我们不熟悉的数域中，如在数域内可以分解为与在实数域内的分解情况完全一致；在数域内只能分解为（x2-2）（x2+2），与在有理数域内的分解情况相同.可
前面的讨论已经知道，数域F上的多项式在F内一定可以分解为一些不可约多项式的乘积.但是，一个多项式在不同数域内的分解情况是不一样的.例如，多项式x4-4，在有理数域Q内可以分解为
（x2-2）（x2+2）；
在实数域R内可以分解为
在复数域C内可以分解为
在一些我们不熟悉的数域中，如在数域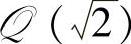
内可以分解为
与在实数域内的分解情况完全一致；在数域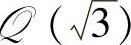
内只能分解为
（x2-2）（x2+2），
与在有理数域内的分解情况相同.可见多项式的因式分解问题是十分复杂的.下面两节我们对多项式在复数域、实数域以及有理数域内的分解作一些初步讨论.
首先，考虑多项式在复数范围内的分解情况.这里我们给出重要的代数基本定理.
定理2.9（代数基本定理） 次数大于零的复系数多项式在复数范围内至少有一个根.
这个定理的证明超出了本书范围，故从略.对证明有兴趣的读者可以参考任何一本初等复分析的书，或者Γ.M.菲赫金哥尔茨的《微积分学教程》第二卷.1799年，著名的德国数学家C.F.Gauss（1777—1855）严格证明了这个定理，他一生对这个定理给出四个证明.
由代数基本定理与推论2.4很容易立刻得到下面推论.
推论2.8 复系数n>0次多项式在复数范围内恰好有n个根.
推论2.9 任意非常数的多项式在复数范围内一定可以分解成一次因式的乘积，即n次多项式f（x）在复数域内可以分解为
的形式，其中a是首项系数，ri是f（x）的λi重根，1≤i≤s，并且λ1+λ2+…+λs=n.
推论告诉我们，复系数多项式在复数范围内必然可以分解成一次因式的乘积.其次，在复数范围内不可约多项式只能是一次多项式.
例2.17 多项式f（x）=x8-1在复数范围内的8个根是
或者用三角函数形式写出是
或者用指数形式写出是
因此，在复数范围内我们有因式分解式
或者
中学代数的一个重要内容是根与系数的关系，著名的Vieta定理说，若x1，x2是一元二次方程ax2+bx+c=0的两个根，那么一定有
这个定理可以推广到更为一般的情况.
定理2.10 若n次多项式f（x）=anxn+…+a1x+a0，其中an≠0，有n个根r1，r2，…，rn（可能相同），则有
更一般地，对每一固定的k，1≤k≤n，总有
证明：由条件及推论2.9可以知道
f（x）=an（x-r1）（x-r2）…（x-rn），
所以，
考虑两边xn-k的系数，左边是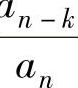
；而右边是n-k个x和r1，r2，…，rn中的k个数相乘得到的，符号是（-1）k.这样就有
特别地，在k=1与k=n时分别得到多项式的所有根的和与积满足等式
证毕.
定理2.11 实系数多项式的虚根一定成对出现，即若虚数r是实系数多项式f（x）的一个根，则
也是f（x）的一个根.
证明：由于f（r）=0，取其共轭复数并注意到f（x）的系数都是实数，则得到
.证毕.
推论2.10 在实数范围内，不可约多项式必是一次或二次的.
证明留作习题.
定理2.12 实系数多项式都可以在实数范围内分解为若干一次或二次的不可约多项式的乘积的形式，即n次实系数多项式f（x）可以分解为
的形式，其中a是首项系数，ri是f（x）的λi重根，1≤i≤s，bj2-4cj<0，1≤j≤t，并且λ1+…+λs+2μ1+…+2μt=n.
例2.18 多项式f（x）=x8-1共有三对共轭复根，它们分别是
依次对应于三个实系数多项式
在实数范围内，有因式分解式
例2.19 设p（x），q（x），r（x）是多项式，满足条件
p（x3）+xq（x3）=（1+x+x2）r（x3）. （2.26）
证明：三个多项式都可被x-1整除.
证明：记多项式x2+x+1的一个复根为ω，则有ω2+ω+1=0及ω3=1.在式（2.26）中，分别令x=ω及
，则有
p（1）+ωq（1）=0，
从中可以解得p（1）=q（1）=0.在式（2.26）中令x=1，可求得r（1）=0.由定理2.8可知x-1可以整除p（x），q（x），r（x）.
例2.20 如果实系数多项式f（x）在R上的值恒大于零，则f（x）一定可以写成两个实系数多项式的平方和的形式.
证明：首先，多项式f（x）在实数范围内没有一次因式，否则会有零点，与恒大于零矛盾.因此，f（x）在实数范围内可以分解为下面的形式：
其中，c>0，λi>0，a2i-4bi<0，1≤i≤s.再注意当a2-4b<0时，必然有
以及简单的代数恒等式
（a2+b2）（c2+d2）=（ac+bd）2+（ad-bc）2，
这样就可以知道结论一定成立.证毕.
尽管代数学基本定理保证一元n次方程在复数范围内一定有n个根，但是把这些根全部找到并不是一件容易的事情.在中学代数课程中，我们学习过一元一次方程与一元二次方程的解法，对于一元一次方程
ax=b，a≠0，
其解为
对于一元二次方程
ax2+bx+c=0，a≠0，(www.chuimin.cn)
其解为
据文献记载，古巴比伦人很早就已经知道公式（2.27）了.但是，一元三次、四次方程的求根公式却在等待了1500多年之后才出现.在1500年左右意大利人Scipi-one dal Ferro（1465—1526）找到了x3+mx=n型的方程的解法.之后，Tartaglia（1499—1557）给出了更一般的三次方程的解法.Lodovico Ferrari（1522—1565）给出了一元四次方程的解法.所有这些结果都发表在Girolamo Cardan（1501—1576）的著作《重要的艺术》（1545年）一书中.
下面我们给出一元三次与四次方程的解法，这里的解法是Vieta最先给出的.首先来求解一元三次方程
x3+bx2+cx+d=0， （2.28）
作变换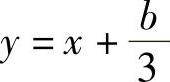
，则方程（2.28）转化为
y3+py+q=0， （2.29）
其中，
显然只要解出方程（2.29）即可.在方程（2.29）中作变换
则得到
从方程（2.31）可以解出六个u的值，但是正好得到三个y的值，进而得到方程（2.28）的全部三个根为
对于求解一元四次方程
x4+bx3+cx2+dx+e=0， （2.32）
作变换
，则方程（2.32）转化为
y4+py2+qy+r=0， （2.33）
其中，
显然只要解出方程（2.33）即可.引入参量z，将方程（2.33）变形为
（y2+z）2=（2z-p）y2-qy+（z2-r）， （2.35）
这表明，右端应该是一个完全平方式，因此
Δ=q2-4（2z-p）（z2-r）=0. （2.36）
方程（2.36）是一个关于参量z的三次方程，求出其全部解，代回方程（2.35）即可解出y，进而解出x.
遗憾的是，五次以上的一元高次方程一般情况下不能用根式求解.1824年，挪威青年数学家Niels Henrik Abel（1802.8.5—1829.4.6）证明了一般五次以上方程不能用代数方法求解.1832年，另一位法国的天才数学家Evariste Galois（1811.10.25—1832.5.31）解决了何种类型的五次以上代数方程可以用根式求解的问题.
习题
2.6.1. 证明推论2.10.
2.6.2. 证明定理2.12.
2.6.3. 求一个次数最低的实系数多项式，使它有三个根1，2+i，
.
2.6.4. 求一个次数最低的实系数多项式，使它有三个根2，i，-2i.
2.6.5. 分别在复数和实数范围内把下列多项式分解因式.
（1）x4+1； （2）x4+4x3+4x2+1；
（3）x6+27； （4）x12-1；
（5）x2n-2xn+2； （6）x2n+xn+1.
2.6.6. 求出下列多项式的全部根.
（1）x4+3x3-2x2+3x+1； （2）2x4-3x3-6x2+3x+2；
（3）x4-3x3-2x2-3x+1； （4）3x4-4x3-10x2+4x+3；
（5）4x6-8x5-9x4+16x3+9x2-8x-4.
2.6.7. 利用根式求解下列方程.
（1）x3-3x+1=0； （2）x3-6x+4=0；
（3）x3+18x2-864=0； （4）x3-16x2+72x-64=0；
（5）x3+15x2-12x+8=0； （6）x3-12x2+7x+4=0.
2.6.8. 利用根式求解下列方程.
（1）x4-15x2-12x-2=0； （2）x4-63x2-22x+840=0；
（3）x4-4x3+3x2+2x-1=0； （4）x4+2x3+8x2+2x+7=0；
（5）x4+6x3+6x2-8=0； （6）x4-x3-3x2+x+1=0.
2.6.9. 设p（x），q（x）是次数不低于n的多项式，p（x）-q（x）的次数最多是n-2，证明：p（x）的所有根的和等于q（x）的所有根的和.
2.6.10. 求一个三次多项式，使其三个根分别是多项式x3+x+1的根的倒数.
2.6.11. 如果三次多项式x3+3px2+3qx+r的根构成调和级数，证明：2q3=r（3pq-r）.
2.6.12. 设x1，x2，x3是三次方程x3-6x2+ax+a=0的根.求：实数a使得
（x1-1）3+（x2-1）3+（x3-1）3=0，
并且对每一个a，求出x1，x2，x3.
2.6.13. 求以三次方程x3+x+1=0的三个根的平方为根的三次方程.
2.6.14. 已知：方程x5-209x+56=0有两个根互为倒数，求出它们.
2.6.15. 设p（x）=xn+an-1xn-1+…+a1x+1是非负系数的实系数多项式，若p（x）有n个实根，证明：p（2）≥3n.
2.6.16. 设pn（x）=p1（pn-1（x）），n≥2，证明：对每一个正整数n，方程pn（x）=x只有互不相同的实根.
2.6.17. 求出所有满足下列条件的多项式p（x）.
（1）p（x2+1）-p2（x）-2xp（x）=0；
（2）p（0）=1.
2.6.18. 求出所有的二次多项式f（x）=ax2+bx+c，使得f（a）=a，f（b）=b且f（c）=c.
有关高等代数的文章
- 详细阅读
-
高等代数中的特征多项式与最小多项式详细阅读
定理10.2 若f（λ）是n阶方阵A的特征多项式，则f=0.证明：设B（λ）是n阶方阵λE-A的伴随矩阵，则利用伴随矩阵的性质有B（λ）=f（λ）E.由于B（λ）的元素都是方阵λE-A的n-1阶子式，因此，都是λ的次数最多是n-1次多项式.这样，B（λ）可以写成如下形式：B（λ）=λn-1B0+λn-2B1+…+an-1A+anE=O.证毕.推论10.1 设线性变换σ的特征多项式是f（λ），那么f（σ）=0.注意 这里f（σ）是一个线性变换.定理10.3 设n阶方阵A的特征多项式是λn+a1λn-1+…......
2023-11-22
-
高等代数：多项式因式分解详细阅读
所谓多项式的因式分解就是把一个多项式写成一些次数较低的多项式的乘积的形式.如同整数的算术基本定理一样，本节将证明数域上的一元多项式环中的唯一分解定理.定义2.7 设f（x）是数域F上的非常数多项式，若存在数域F上的两个非常数多项式g（x），h（x），使得f（x）=g（x）h（x），则称f（x）是数域F上的可约多项式.否则，f（x）就称为数域F上的不可约多项式.多项式是否可约和数域F的选取密切相关.......
2023-11-22
-
高等代数：对称多项式及其应用详细阅读
，xn的对称多项式称为n元初等对称多项式.通常，这n个初等对称多项式依次记作σ1，σ2，…，σn.初等对称多项式是最基本的对称多项式.在一元多项式根与系数的关系中，就会自然地出现初等对称多项式.以x1，x2，…，xn的初等对称多项式.证明：存在性.设对称多项式f（x1，x2，…......
2023-11-22
-
高等代数：多项式的带余除法运算详细阅读
正如整数的除法在整数范围内不能畅通无阻地进行一样，多项式的除法也不是总可以进行的.但是，我们可以类似于整数的带余除法引入多项式之间的带余除法运算.定理2.1 设f（x），g（x）是数域F上的两个多项式，且g（x）≠0，则存在数域F上的多项式q（x），r（x），使得f（x）=q（x）g（x）+r（x）， （2.7）其中r（x）=0或者degr（x）
2023-11-22
-
地基变形系数与稳定安全系数的内在联系详细阅读
考虑到通常情况下侧向变形、竖向沉降较大值分别发生于下坡脚处地基剖面、地基顶面附近，故本节暂取下坡脚处地基剖面最大向外侧向变形与地基顶面最大向下竖向沉降之比值为地基变形系数K。图5-2为4种地基条件下地基变形系数与稳定安全系数关系曲线。......
2023-10-03
-
多项式的根及其在高等代数中的应用详细阅读
+a1α+a0∈F称为多项式f在x=α处的值，记作f（α）=anαn+an-1αn-1+…，αn+1是n次多项式f的不同的根.显然，x-αi一定两两互素，因此，f=q…，考虑多项式两端的次数可以看到只有f=0.证毕.推论2.6 若两个n次多项式在n+1个不同的点取值相同，则它们必相等.证明：设f，g是数域F上的n次多项式，且在n+1个不同的点αi，i=1，2，…......
2023-11-22
-
耦合系数与同名端的影响详细阅读
漏磁通的多少表明了两个线圈之间耦合的紧密程度。图6.3表示了绕向和同名端的关系。图6.3两线圈绕向与同名端的关系检验学习结果6.1.1 写出图6.1和图6.2中线圈2两端的互感电压u2。......
2023-06-24
相关推荐