在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会......
2023-11-22
高等代数：多项式的带余除法运算
【摘要】：正如整数的除法在整数范围内不能畅通无阻地进行一样，多项式的除法也不是总可以进行的.但是，我们可以类似于整数的带余除法引入多项式之间的带余除法运算.定理2.1 设f（x），g（x）是数域F上的两个多项式，且g（x）≠0，则存在数域F上的多项式q（x），r（x），使得f（x）=q（x）g（x）+r（x）， （2.7）其中r（x）=0或者degr（x）
正如整数的除法在整数范围内不能畅通无阻地进行一样，多项式的除法也不是总可以进行的.但是，我们可以类似于整数的带余除法引入多项式之间的带余除法运算.
定理2.1 设f（x），g（x）是数域F上的两个多项式，且g（x）≠0，则存在数域F上的多项式q（x），r（x），使得
f（x）=q（x）g（x）+r（x）， （2.7）
其中r（x）=0或者degr（x）<degg（x），并且多项式q（x），r（x）是由f（x），g（x）唯一确定的.
证明：存在性.当degg（x）=0时，g（x）=a≠0∈F，则有
取多项式
即可得到所要结论.
当degg（x）=m>0时，我们对f（x）的次数用数学归纳法.当degf（x）<degg（x）时，取
q（x）=0，r（x）=f（x）
即可得到结论.当degf（x）≥degg（x）时，不妨设f（x）是n次多项式，且首项系数为b，g（x）的首项系数为a.作多项式
它是数域F上的多项式且次数小于n，由归纳假设，存在数域F上的多项式q1（x），r1（x）使得
其中r1（x）=0或者degr1（x）<degg（x）.这时取多项式
则显然q（x），r（x）为数域F上的多项式且
f（x）=q（x）g（x）+r（x），
这时显然有r（x）=0或者degr（x）<degg（x）.
唯一性.若另有多项式q1（x），r1（x）使得
f（x）=q1（x）g（x）+r1（x）， （2.8）
且其中r1（x）=0或者degr1（x）<degg（x）.式（2.7）、式（2.8）两式相减得
（q（x）-q1（x））g（x）=r1（x）-r（x）， （2.9）
若q（x）-q1（x）≠0，则由式（2.9）可以得到
deg[（q（x）-q1（x））g（x）]>deg（r1（x）-r（x）），
这是不可能的.因此，q（x）-q1（x）=0，即q（x）=q1（x），进而有r（x）=r1（x）.
证毕.
定理2.1中叙述的多项式除法称为多项式的带余除法，定理中的多项式q（x）称为g（x）除f（x）的商，多项式r（x）称为余式.多项式的带余除法运算也可以利用竖式形式完成，其竖式格式为
例2.3 设
f（x）=2x3+3x2-7x+1
和
g（x）=3x2-2x-1，
则g（x）除f（x）的商式是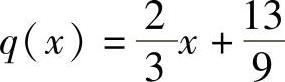
，余式是
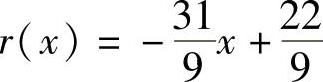，即有
竖式格式计算过程为
这种计算也可以使用分离系数法完成，格式如下：
例2.4 利用分离系数法计算多项式
f（x）=2x6-2x5-27x4+7x3+11x2+9x-1
除以多项式
g（x）=x2+3x-1
的商式和余式.
解：使用分离系数法，列竖式计算得到
所以多项式f（x）除以g（x）的商式是2x4-8x3-x2+2x+4，余式是-x+3.
例2.5 多项式的带余除法和所考虑的多项式系数的范围有关.例如，在整系数多项式范围内，定理2.1就不成立.例如，取f（x）=2x2，g（x）=3x+2，就无法找到满足定理2.1要求的整系数多项式q（x）和r（x）.
在考虑多项式的除法运算时会出现所谓除不尽的情况，因此恰好除尽，也就是余式为零多项式的情况是格外重要的.这时我们可以引入一个重要的概念——整除.
定义2.1 设f（x），g（x）是数域F上的多项式，如果存在数域F上的多项式q（x），使得f（x）=q（x）g（x），则称多项式g（x）整除f（x），记作g（x）|f（x）.此时，g（x）称为f（x）的因式，f（x）称为g（x）的倍式.
例2.6 设f（x）=x3-6x2+11x-6，g（x）=x2-3x+2，由于f（x）=（x-3）g（x），则有g（x）|f（x）.
容易验证整除性的如下性质.
命题2.3 设f（x），g（x）和h（x）是数域F上的多项式，那么有如下一些结论.
（1）f（x）|f（x）；
（2）若f（x）|g（x），g（x）|h（x），则f（x）|h（x）；(www.chuimin.cn)
（3）若f（x）|g（x），g（x）|f（x），则f（x）=cg（x），c是F中的一个非零数；
（4）若f（x）|g（x），f（x）|h（x），则f（x）|（g（x）±h（x））；
（5）若f（x）|g（x），则f（x）|g（x）h（x）.
证明：（1）由于f（x）=1·f（x），因此f（x）|f（x）.
（2）若f（x）|g（x），g（x）|h（x），那么一定有多项式q1（x），q2（x）使得
g（x）=q1（x）f（x），h（x）=q2（x）g（x）.
因此，代入得到
h（x）=q2（x）q1（x）f（x），
由整除定义知道f（x）|g（x）.
（3）若f（x），g（x）中有一个是零多项式，那么可以推出另一个也必然是零多项式.这时结论成立.
若f（x），g（x）都不是零多项式，由于f（x）|g（x），g（x）|f（x），那么一定有多项式q1（x），q2（x）使得
g（x）=q1（x）f（x），f（x）=q2（x）g（x）.
因此我们可以得到
f（x）=q2（x）q1（x）f（x），
由消去律有q2（x）q1（x）=1，由命题2.1的（3）可以看出
degq2（x）+degq1（x）=0，
这表明q2（x）一定是非零数.
（4）若f（x）|g（x），f（x）|h（x），那么一定有两个多项式q1（x），q2（x）使得
g（x）=q1（x）f（x），h（x）=q2（x）f（x），
于是就得到
g（x）±h（x）=（q1（x）±q2（x））f（x），
由整除的定义可以看到f（x）|（g（x）±h（x））.
（5）条件表明存在多项式q（x）使得g（x）=q（x）f（x），而这时必然有g（x）h（x）=q（x）h（x）f（x），因此f（x）|g（x）h（x）.
证毕.
习题
2.2.1. 计算多项式f（x）除以g（x）的商和余式.
（1）f（x）=2x2+7x+9，g（x）=2x+1；
（2）f（x）=x4-5x3+2x2-6x-7，g（x）=x2-2x-3；
（3）f（x）=x4+x2+1，g（x）=x2+x+1；
（4）f（x）=2x4+3x2-7x+8，g（x）=2x2-2x+1；
（5）f（x）=4x3+x2，g（x）=x+1+i，i2=-1；
（6）f（x）=x4+x2+1，g（x）=ix2+（1+i）x-1，i2=-1.
2.2.2. 判断多项式
f（x）=x4+2x3-13x2-14x+24
是否可以被下面的多项式整除？如果不能的话，请给出余式.
（1）x+3； （2）x-1；
（3）x2-3x+2； （4）x2+6x+8.
2.2.3. 给出多项式（x-1）2整除x4+ax2+b的条件.
2.2.4. 当p，q，m满足什么条件时，x2+mx-1|x3+px+q.
2.2.5. 对哪些自然数k，x2-1|xk-1？
2.2.6. 请给出xp-1|xk-1的充分必要条件，其中p是已知素数.
2.2.7. 证明：x|fk（x）的充分必要条件是x|f（x）.
2.2.8. 求出多项式2xn+2-（n+2）x2+n除以（x-1）2的商.
2.2.9. 证明多项式f（x）=a0xn+…+an-1x+an能被（x-1）k+1整除的充分必要条件是
有关高等代数的文章
- 详细阅读
-
高等代数：多项式的有理与整系数详细阅读
一个有理系数多项式anxn+…，bn的最大公因数是1.这样的工作总是能够完成的，如我们可以先形式上通分，然后把分母以及分子系数的公因数同时提出.由此可见，有理系数多项式anxn+…+b1x+b0的因式分解问题.以下我们只讨论整系数多项式的因式分解问题.首先我们引入本原多项式的概念.定义2.10 若整系数非零多项式f=anxn+…......
2023-11-22
-
高等代数：多项式因式分解详细阅读
所谓多项式的因式分解就是把一个多项式写成一些次数较低的多项式的乘积的形式.如同整数的算术基本定理一样，本节将证明数域上的一元多项式环中的唯一分解定理.定义2.7 设f（x）是数域F上的非常数多项式，若存在数域F上的两个非常数多项式g（x），h（x），使得f（x）=g（x）h（x），则称f（x）是数域F上的可约多项式.否则，f（x）就称为数域F上的不可约多项式.多项式是否可约和数域F的选取密切相关.......
2023-11-22
-
高等代数中的特征多项式与最小多项式详细阅读
定理10.2 若f（λ）是n阶方阵A的特征多项式，则f=0.证明：设B（λ）是n阶方阵λE-A的伴随矩阵，则利用伴随矩阵的性质有B（λ）=f（λ）E.由于B（λ）的元素都是方阵λE-A的n-1阶子式，因此，都是λ的次数最多是n-1次多项式.这样，B（λ）可以写成如下形式：B（λ）=λn-1B0+λn-2B1+…+an-1A+anE=O.证毕.推论10.1 设线性变换σ的特征多项式是f（λ），那么f（σ）=0.注意 这里f（σ）是一个线性变换.定理10.3 设n阶方阵A的特征多项式是λn+a1λn-1+…......
2023-11-22
-
高等代数：对称多项式及其应用详细阅读
，xn的对称多项式称为n元初等对称多项式.通常，这n个初等对称多项式依次记作σ1，σ2，…，σn.初等对称多项式是最基本的对称多项式.在一元多项式根与系数的关系中，就会自然地出现初等对称多项式.以x1，x2，…，xn的初等对称多项式.证明：存在性.设对称多项式f（x1，x2，…......
2023-11-22
-
多项式的根及其在高等代数中的应用详细阅读
+a1α+a0∈F称为多项式f在x=α处的值，记作f（α）=anαn+an-1αn-1+…，αn+1是n次多项式f的不同的根.显然，x-αi一定两两互素，因此，f=q…，考虑多项式两端的次数可以看到只有f=0.证毕.推论2.6 若两个n次多项式在n+1个不同的点取值相同，则它们必相等.证明：设f，g是数域F上的n次多项式，且在n+1个不同的点αi，i=1，2，…......
2023-11-22
-
复系数与实系数多项式-《高等代数》简介详细阅读
前面的讨论已经知道，数域F上的多项式在F内一定可以分解为一些不可约多项式的乘积.但是，一个多项式在不同数域内的分解情况是不一样的.例如，多项式x4-4，在有理数域Q内可以分解为（x2-2）（x2+2）；在实数域R内可以分解为在复数域C内可以分解为在一些我们不熟悉的数域中，如在数域内可以分解为与在实数域内的分解情况完全一致；在数域内只能分解为（x2-2）（x2+2），与在有理数域内的分解情况相同.可......
2023-11-22
- 详细阅读
相关推荐