首页理论教育数域中的高等代数，证明与习题解答

数域中的高等代数，证明与习题解答

2023-11-22 理论教育版权反馈

【摘要】：，这说明零与负整数都属于F.至此可以得到整数集合ZF.再由除法的封闭性，以及任何有理数都可以写成两个整数的商，这样就得到有理数域QF.证毕.该定理表明，从包含关系上说有理数域是最小的数域.习题1.5.1. 证明：，都是无理数.1.5.2. 设p1，p2，…

在中学数学里，我们学过复数.复数是如下定义的：若a，b是实数，那么形如a+bi，的表达式称为复数.若b≠0，则a+bi称为虚数；若a=0，b≠0，则bi称为纯虚数.复数的四则运算法则如下：

（a+bi）+（c+di）=（a+c）+（b+d）i，

（a+bi）-（c+di）=（a-c）+（b-d）i，

（a+bi）（c+di）=（ac-bd）+（ad+bc）i，

在这组公式里，a，b，c，d都是实数.

在数学里，域是一个对加、减、乘、除四种运算都封闭的代数结构.我们比较熟悉的有有理数域、实数域、复数域，通常依次记为Q，R，C.

定义1.10 若F是复数域C的无限子集，并且F对复数的加法、减法、乘法、除法（除数不为零）运算封闭，那么就称F是一个数域.

例1.22 记F={a+bi|a，b∈Q，i²=-1}，则F是一个数域.这个数域通常记作Q（i）.

例1.23 证明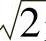：是无理数.

证明：用反证法.设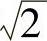是有理数，即可以写成的形式，p，q是互素的正整数.那么，2p²=q²，此式说明q是偶数，记q=2q₁，则有p²=2q²₁，这又表明p也是偶数，这与p，q互素矛盾.于是，我们证明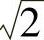是无理数.

例1.24 证明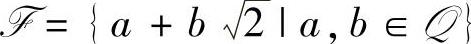：是一个数域，这个数域通常记作Q.

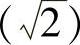证明：设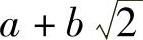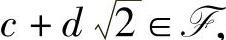，，那么a，b，c，d∈Q，这时有

容易看到

都是有理数.因此，F是一个数域.(www.chuimin.cn)

定理1.6 任何数域都包含有理数域.

证明：设F⊆C是一个数域，我们来证明有理数域Q一定包含于F.

首先，由数域的定义知道F中一定有一个非零数a≠0，由于数域对除法运算封闭，因此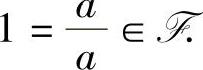数域对加法运算封闭，因此2=1+1∈F，3=2+1∈F，…，这说明所有自然数都属于F.再由数域对减法运算封闭，得到0=1-1∈F，-1=0-1∈F，…，这说明零与负整数都属于F.

至此可以得到整数集合Z⊆F.再由除法的封闭性，以及任何有理数都可以写成两个整数的商，这样就得到有理数域Q⊆F.证毕.

该定理表明，从包含关系上说有理数域是最小的数域.

习题

1.5.1. 证明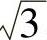：，都是无理数.

1.5.2. 设p₁，p₂，…，p_n是n个互不相同的素数，证明：是无理数.

1.5.3. 证明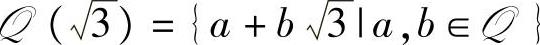：是一个数域.

1.5.4. 证明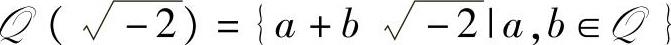：是一个数域.

1.5.5. 证明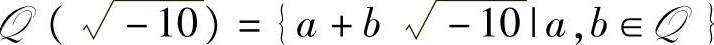：是一个数域.

1.5.6. 记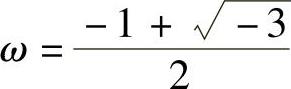，证明：Q（ω）={a+bω|a，b∈Q}是一个数域.

1.5.7. 从包含关系上说，含有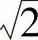2的最小的数域是什么？