数学归纳法：自然数应用

2023-11-22 理论教育版权反馈

【摘要】：自然数1，2，3，…

自然数1，2，3，…是我们最先认识到的数，是我们日常计数的工具，也是代数学研究的基础.通常把全体自然数组成的集合，记作N.自然数来源于我们对计数的需要，在这里我们对自然数集合N给出一个公理化的定义，其目的在于更深入地认识自然数的本质.

意大利数学家Peano在1889年提出了如下一组公理来定义自然数集合N，称之为Peano公理.

Peano公理自然数集N是满足下述条件的集合，

Ⅰ.1是自然数；

Ⅱ.每一个自然数n都有一个确定的后继，记作n⁺；

Ⅲ.没有一个自然数的后继是1；

Ⅳ.如果n⁺=m⁺，则n=m；

Ⅴ.由自然数组成的每个集合，如果它含有1；并且含有集合中每个自然数的后继.那么，这个集合一定是自然数集合.

在这组公理中，公理Ⅴ称为归纳公理，它是我们通常所使用的数学归纳法的基础.归纳公理也可以写成下面的形式：

V’.若S⊆N，且满足条件：

（ⅰ）1∈S；

（ⅱ）若n∈S，则n+∈S，那么，S=N.

在Peano公理中，所谓n的后继n+也就是n+1.在以这组公理定义了自然数之后，可以用代数方法建立有理数系.归纳公理的一个最直接用处是导致我们熟知的数学归纳法.

数学归纳法原理设P是一个与自然数有关的命题，且

（1）P（1）成立；

（2）如果P（n）成立，那么P（n+1）也成立，则命题P对所有的自然数都成立.

证明：记S={n∈N|P（n）成立}，即S是使得命题P成立的所有自然数组成的集合.由条件（1）1∈S；由条件（2）如果n∈S，那么，n+∈S.由归纳公理可以知道这时必然有S=N，即命题P对所有的自然数都成立.证毕.

第二数学归纳法原理设P是一个与自然数有关的命题，且

（1）P（1）成立；

（2）如果P（1），P（2），…，P（n）成立，那么P（n+1）也成立，则命题P对所有的自然数都成立.

证明留作习题.

例1.18（Cauchy不等式）设a₁，a₂，…，a_n；b₁，b₂，…，b_n是两组实数，证明：

也即

（a₁b₁+a₂b₂+…+a_nb_n）2≤（a²₁+a²₂+…+a²_n）（b²₁+b²₂+…+b²_n）.

在这个不等式中，等号当且仅当两组数对应成比例，即

时成立.

证明：用数学归纳法.

当n=1时，不等式是平凡的.

假设当n=k时不等式成立，即

当n=k+1时，我们有

不等式也成立.由归纳法可知不等式总是成立的.

注意到在证明过程中，不等号处使用了归纳假设与算术-几何平均值定理，因此，等号成立的充分必要条件是a_ib_k+1=b_ia_k+1，对每个i都成立，也即两组数a₁，a₂，…，a_n；b₁，b₂，…，b_n对应成比例.证毕.

例1.19 证明Fermat小定理：若p是素数，a是正整数，（a，p）=1，那么a^p-1≡1（modp）.

证明：我们先用数学归纳法证明命题：若p是素数，a是正整数，那么a^p≡a（modp）.

当a=1时结论显然成立.假设当a=k时结论成立，即k^p≡k（modp）.那么当a=k+1时，由二项式定理有

由于p是素数，那么容易验证

因此由式（1.1）可以看到

（k+1）p≡k^p+1≡k+1（modp）.

因此得到若a是正整数，那么a^p≡a（modp）.

当（a，p）=1时，也有a^p≡a（modp），约去a就是a^p-1≡1（modp）.证毕.

例1.20 有两堆个数一样的棋子，甲、乙两人分别依次取之，规则为：每次取几颗棋子都可以，但是只能从一堆里面取，取到最后一颗棋子的获胜.问：有无制胜的办法？

证明：后取者必然获得胜利.

对每堆棋子的个数k用归纳法证明后取者必然获胜.当k=1时，结论显然成立.假设当k≤n时，结论总是成立的.那么当k=n+1时，若先取者取走l，1≤l≤n+1，颗棋子，那么后取者则从另一堆中也取走l颗棋子.这时，每堆棋子都有n+1-l颗，使用归纳假设，后取者获胜.证毕.

自然数的另一条基本性质称为最小数原理.

最小数原理自然数的任意非空子集一定包含一个最小数.

证明：设S⊆N，且S≠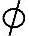，下面来证明S中一定有一个最小的数.用反证法，假设S中没有最小数，作集合

T={n|对一切k∈N，1≤k≤n，k∉S}.

我们有

（1）1∈T.由于S中没有最小数，所以1∉S.而不超过1的自然数只有1，因此，1∈T.(www.chuimin.cn)

（2）如果n∈T，则n+1∈T.此时因为n∈T，所以，不超过n的自然数都不在S中，如果n+1∈S，那么n+1就是S中的最小数，与S中没有最小数矛盾.所以，n+1∈T.

由（1）、（2）及归纳公理可知T=N.也就是说，S=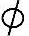，与题设矛盾.所以假设不对，即S中一定有最小数.证毕.

例1.21 证明：不定方程

2x³+4y³=z³ （1.2）

没有正整数解.

证明：用反证法.假设这个不定方程有正整数解，由最小数原理，必然有一组使得z取值最小的解，不妨记这组解为

x=x₀，y=y₀，z=z_0.

那么就必然有

2x³₀+4y³₀=z₀³. （1.3）

显然，式（1.3）左边是偶数，因此右边z₀³一定是偶数，也就是说z₀一定是偶数，我们记z₀=2z₁，这里z₁是整数.

把z₀=2z₁代入式（1.3）并化简得到

x₀³+2y₀³=4z³₁，（1.4）

即x³₀=4z³₁-2y³₀，这表明x₀也是偶数，于是可以记x₀=2x₁，x₁是整数.

把x₀=2x₁代入方程（1.4），并化简得到

4x³₁+y₀³=2z³₁，（1.5）

同样道理说明y₀也是偶数，再记y₀=2y₁，y₁是整数.

把y₀=2y₁代入方程（1.5），并化简得到

2x³₁+4y³₁=z³₁，（1.6）

式（1.6）表明不定方程（1.2）有一组解

x=x₁，y=y₁，z=z₁，

但是这里z₁<z₀与z₀的选择矛盾，因此假设错误.这即得到不定方程（1.2）没有正整数解.

例1.21的证明方法称为无穷下降法（infinite descent），这是Fermat最先使用的，他用这个方法证明了不定方程x⁴+y⁴=z⁴没有正整数解.

习题

1.4.1. 证明：若a_i>0，1≤i≤n，则

1+a₁+a₂+…+a_n≤（1+a₁）（1+a₂）…（1+a_n）.

1.4.2. 设0≤x_i≤1，i=1，2，…，n，证明：

2^n-1（1+x₁x₂…x_n）≥（1+x₁）（1+x₂）…（1+x_n），

并证明当且仅当这n个数中有n-1个都等于1时等号成立.

1.4.3. 证明：1³+2³+3³+…+n³=（1+2+…+n）².

1.4.4. 证明：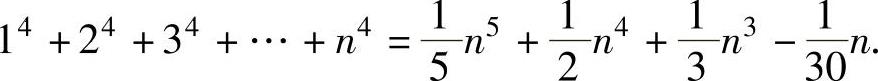

1.4.5. 证明第二数学归纳法.

1.4.6. 数列{F_n}满足条件：F₀=F₁=1，F_n=F_n-1+F_n-2，n≥2.证明：

数列{F_n}称为Fibonacci数列.

1.4.7. 数学归纳法有多种形式，下面这种形式是Cauchy最先使用的，他利用这种方法证明了算术-几何平均值不等式.

（1）设P是一个与自然数有关的命题，且

1）对所有的自然数n，P（2ⁿ）成立；

2）当k<2ⁿ时，P（k）也成立，

则命题P对所有的自然数都成立.

（2）证明算术-几何平均值不等式，即若a₁，a₂，…，a_n都是正数，则

1.4.8. （双重数学归纳法）设P（m，n）是一个定义在自然数集合上的命题，满足条件

（1）P（1，1）成立；

（2）若P（m，1）成立，那么P（m+1，1）成立；

（3）若P（m，n）对所有m成立，那么P（m，n+1）对所有m也成立，那么对所有自然数m，n，命题P（m，n）都成立.

1.4.9. 若p是一个素数，那么不定方程px³+p²y³=z³没有正整数解.

1.4.10. 设S₁，S₂，…，S_n，…是一个边长都是正整数的长方形序列，证明：一定可以从中选出一个子序列，使得子序列中的每个长方形可以套在它后面一个长方形中.

1.4.11. 用更多的方法证明Cauchy不等式.

1.4.12. Cauchy不等式在复数范围内也成立，即若a₁，a₂，…，a_n；b₁，b₂，…，b_n是两组复数，那么

在这个不等式中，等号当且仅当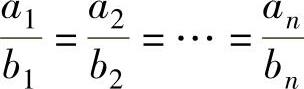时成立.

数学归纳法：自然数应用

相关推荐