【摘要】:,umn+1中,或者存在一个长度大于m的减子数列,或者存在一个长度大于n的增子数列.证明:分别用l-i,l-i表示从ui开始的最长的减子数列和最长的增子数列的长度.假设命题的结论是错误的,即每个减子数列的长度不超过m,并且每个增子数列的长度不超过n.定义一
定义1.8 设X,Y是非空集合,所谓映射f是集合X,Y以及X和Y的元素之间的一个对应法则f,依照这个法则,X中的每一个元素x都对应于Y中唯一确定的一个元素y.映射通常记作f:X→Y.X称为映射f的定义域,Y称为映射f的值域.
在这个对应关系中,若x∈X对应于y∈Y,记作y=f(x)或f:x y,y叫作x的像,x叫作y的原像.集合{f(x)|x∈X}称为映射f的像,记作f(X)或Imf.若y∈Y,集合{x|f(x)=y}称为y的原像,记作f-1(y).
y,y叫作x的像,x叫作y的原像.集合{f(x)|x∈X}称为映射f的像,记作f(X)或Imf.若y∈Y,集合{x|f(x)=y}称为y的原像,记作f-1(y).
定义1.9 如果Imf=Y,则称f为满射;如果x1≠x2,则f(x1)≠f(x2),称f为单射.如果f既是满射,又是单射,则称为双射.
定理1.4 若f是X到Y的映射,
(1)f是单射当且仅当对任意的x1,x2∈X,如果f(x1)=f(x2),则x1=x2;
(2)f是满射当且仅当对任意的y∈Y,存在x∈X,使得y=f(x).
此定理的证明是相当简单的,故从略.
若X,Y都是数集,从X到Y的映射称为函数.设X,Y,Z都是非空集合,映射f:X→Y,g:Y→Z,定义一个新映射记作g f,
f,
g f:X→Z,x
f:X→Z,x g(f(x))
g(f(x))
称为映射g与f的复合映射.若f都是非空集合X到自身上的映射,那么复合映射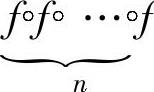 f记作fn.
f记作fn.
定理1.5 设A,B,C,D是非空集合,f:A→B,g:B→C,h:C→D,那么,有等式
h (g
(g f)=(h
f)=(h g)
g) f
f
成立.也就是说,映射的复合运算满足结合律.
证明:显然映射h (g
(g f)与(h
f)与(h g)
g) f都是从A到D的映射.
f都是从A到D的映射.
设A中元素xA在f之下的像是xB,xB在g之下的像是xC,xC在h之下的像是xD,即
f(xA)=xB,g(xB)=xC,h(xC)=xD.
那么根据复合映射的定义,g f将把xA对应到xC,h
f将把xA对应到xC,h g将把xB对应到xD,即
g将把xB对应到xD,即
g f(xA)=xC,h
f(xA)=xC,h g(xB)=xD.
g(xB)=xD.
因此我们有
h (g
(g f)(xA)=h(xC)=xD,
f)(xA)=h(xC)=xD,
以及
(h g)
g) f(xA)=(h
f(xA)=(h g)(xB)=xD.
g)(xB)=xD.
由此可见,h (g
(g f)=(h
f)=(h g)
g) f.证毕.
f.证毕.
若X,Y是非空集合,映射f:X→Y,g:Y→X,则g f和f
f和f g都有定义.但是g
g都有定义.但是g f和f
f和f g是不同的映射.
g是不同的映射.
设X是一个非空集合,所谓恒等映射,通常记作iX或简记作i(也可记作e,1),定义为iX:X→X,x x或iX(x)=x,i(x)=x.
x或iX(x)=x,i(x)=x.
设f是非空集合X到自身上的双射,定义一个对应关系g:X→X,y x,这里,y=f(x).容易验证g是一个映射,也是双射,并且f
x,这里,y=f(x).容易验证g是一个映射,也是双射,并且f g=g
g=g f=iX.映射g称为映射f的逆映射,记作f-1.函数的逆映射(如果存在)叫作反函数.
f=iX.映射g称为映射f的逆映射,记作f-1.函数的逆映射(如果存在)叫作反函数.
例1.10f,g,h是实数集合R上的映射,也就是函数,定义如下:
f(x)=2x+1,g(x)=ex,h(x)=x2+1.
由于h(1)=h(-1)=2,因此h不是单射.又由于h(x)≥1≠0,因此零不可能有原像,h不是满射.
显然,g(x)>0,因此g不是满射.对实数x1,x2,如果g(x1)=g(x2),即ex1=ex2,那么有ex1-x2=1,因此有x1-x2=0,即x1=x2.这表明g是单射.
对任意的实数y,显然有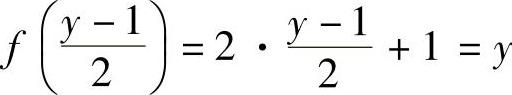 ,因此f是满射.另一方面,对于两个实数x1,x2,若f(x1)=f(x2),即2x1+1=2x2+1,因此x1=x2.这表明f是单射.映射f既满且单,因此是一个双射.容易计算出f的反函数是
,因此f是满射.另一方面,对于两个实数x1,x2,若f(x1)=f(x2),即2x1+1=2x2+1,因此x1=x2.这表明f是单射.映射f既满且单,因此是一个双射.容易计算出f的反函数是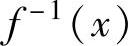
 .
.
另外,简单计算还有
f f(x)=4x+3,f
f(x)=4x+3,f g(x)=2ex+1,g
g(x)=2ex+1,g f(x)=e2x+1,
f(x)=e2x+1,
以及
fn(x)=2n(x+1)-1.
例1.11(Eulerϕ-函数) 定义在自然数集合N上的函数称为数论函数.函数ϕ:N→N称为Eulerϕ-函数,如果ϕ(n)等于不超过n的与n互素的自然数的个数.
通过简单的计算可以得到ϕ(1)=1,ϕ(2)=1,ϕ(3)=2,ϕ(4)=2,ϕ(5)=4,ϕ(6)=2,ϕ(7)=6,ϕ(8)=4,ϕ(9)=6,ϕ(10)=4等.
另外,还有ϕ-1(1)={1,2},ϕ-1(2)={3,4,6},ϕ-1(3)= 等.求出集合Imϕ是一个困难的数学问题.
等.求出集合Imϕ是一个困难的数学问题.
例1.12 用[x]表示实数x的整数部分,即不超过x的最大整数.函数f:R→Z,x [x],f称为取整函数.例如,[4]=4,[5.7]=5,[-π]=-4等.
[x],f称为取整函数.例如,[4]=4,[5.7]=5,[-π]=-4等.
例1.13(3n+1映射) 定义数论函数C如下,C:N→N,
这个映射C称为3n+1映射或Collatz映射.(www.chuimin.cn)
容易计算C(1)=2,C(2)=1,C(3)=5,C(4)=2,C(5)=8,…,C(18)=9,C(19)=29等.映射C是满射,但不是单射,这是因为C(3)=C(10)=5,C-1(5)={3,10},C-1(6)={12}.
一个著名的猜想是对任意的自然数n,一定存在自然数k,使得Ck(n)=1,这个猜想称为3n+1猜想.
例1.14 在平面直角坐标系OXY中,由所有的圆心在坐标原点的同心圆组成的集合记作A.这样的圆可以由它们的半径r决定,记为O(r),那么A={O(r)|r>0}.
建立从实数集合R到集合A的映射f:R→A,x O(ex).显然,映射f是双射,它的逆映射是f-1:A→R,O(r)
O(ex).显然,映射f是双射,它的逆映射是f-1:A→R,O(r) lnr.
lnr.
例1.15 记A={(x,y)|x2+y2=1},定义映射f如下:
f:[0,2π)→A,t (cost,sint).
(cost,sint).
映射f是双射,其逆映射
这一对应关系也可以写作
(x,y) π(1-sgny)+arccosx·sgny.
π(1-sgny)+arccosx·sgny.
例1.16 本例试图在一个单位圆周与直线之间建立一个双射.在平面直角坐标系OXY中,集合
A={(x,y)|x2+y2=1且y≠1},B={(x,0)|x∈R}.
对单位圆周上的任意一个异于(0,1)的点(x,y),连接(0,1)、(x,y)的直线交直线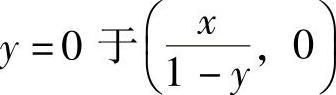 .建立映射
.建立映射
可以验证f是双射.f的逆映射f-1是
例1.17(Erdös Szekeres) 在一个有mn+1个各不相同的整数的数列u1,u2,…,umn+1中,或者存在一个长度大于m的减子数列,或者存在一个长度大于n的增子数列.
证明:分别用l-i,l-i表示从ui开始的最长的减子数列和最长的增子数列的长度.假设命题的结论是错误的,即每个减子数列的长度不超过m,并且每个增子数列的长度不超过n.
定义一个从集合{u1,u2,…,umn+1}到笛卡儿积{1,2,…,m}×{1,2,…,n}的映射f如下:
下面我们来证明f是单射.
假定i<j.在这个情形下,ui>uj就蕴涵l-i>l-j.因为我们至少可以加一个元素(即ui)到从ui开始的最大长度的减子数列的左边,从而得到一个从ui开始的更长的减子数列,所以l-i>l-j.类似地,ui<uj就蕴涵l+i>l+j.因为我们至少可以加一个元素(即ui)到从ui开始的最大长度的增子数列的左边,从而得到一个从ui开始的长度更大的增子数列,所以l+i>l+j.因此ui≠uj就蕴涵(u-i,u+i)≠(u-j,u+j).因为这些有序对中至少有一个位置上的数是不同的.最后这个不等式就意味着f(ui)≠f(uj).这样就证明了f是单射.
集合{u1,u2,…,umn+1}中有mn+1个元素,笛卡儿积集{1,2,…,m}×{1,2,…,n}中有mn个元素,f是单射表明mn+1≤mn,但这是不可能的.
习题
1.3.1. 若X是一个含有n个元素的集合,试问从X到自身的映射有多少个?其中有多少个是双射?
1.3.2. 证明:例1.14中给出的映射f是双射.
1.3.3. 证明:例1.16中的映射f是双射.
1.3.4. 若f g是一个单射,证明g也是单射;若f
g是一个单射,证明g也是单射;若f g是一个满射,证明g也是满射.
g是一个满射,证明g也是满射.
1.3.5. 若X,Y都是有限集合,f是从X到Y的映射,分别以|X|,|Y|表示集合X,Y含有的元素的个数.证明:当f是单射时,|X|≤|Y|;当f是满射时,|X|≥|Y|;进而当f是双射时,|X|=|Y|.
1.3.6. 若X是一个有限集,f是其上的映射.证明:f是单射的充分必要条件是f是满射.
1.3.7. 画出函数[x]的图形.
1.3.8. 在空间直角坐标系OXYZ中,集合
A={(x,y,z)|x2+y2+z2=1且z≠1},B={(x,y,0)|x,y∈R}.试建立集合A与B之间的双射,并求出它的逆映射.
1.3.9. 设函数f:R→R,f(x)=5x+3.求:
(1)f(5),f(-2);
(2)f([0,1]),f((-10,9]);
(3)f-1(0),f-1(9);
(4)f-1([0,1]),f-1((-10,9]);
(5)fn(x)及其反函数.
1.3.10. 设函数f:R→R,f(x)=-x2+4.求:
(1)f(5),f(-2); (2)f([0,1]),f((-10,9]);
(3)f-1(0),f-1(9); (4)f-1([0,1]),f-1((-5,2]).
1.3.11. 设函数f如例1.12定义,求:f-1(3),f-1({-2,2}).





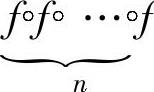
 (
(


 (
(






 (
(



 (
(









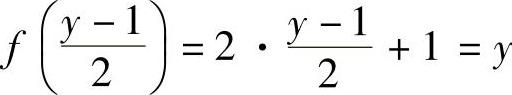 ,因此
,因此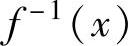




 等
等 [
[
 ln
ln (cos
(cos π(1-sgn
π(1-sgn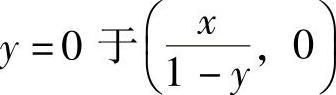 .建立映射
.建立映射







相关推荐