精度等级GB/T 11365—1989规定了12个精度等级，按精度高低依次为1、2、…与圆柱齿轮公差相同，标准将锥齿轮和齿轮副的公差项目也分成三个公差组，见表7-39。根据使用要求，允许各公差组选用不同的精度等级。允许工作齿面与非工作齿面选用不同的精度等级。GB/T 11365—1989规定的各精度等级各项公差数值见表7-40至表7-55。表7-38 齿轮、齿轮副误差及侧隙的定义与代号图4-6非门电路符号国标符号；、习惯画法......
2025-09-29
高等代数中集合与其运算-高等代数
【摘要】：在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2008年北京奥运会
在数学中，有许多概念是不定义概念，如几何学中的点、线、面等概念.集合与元素是集合论的基本概念，也是一对不定义概念.集合论是著名的德国数学家George Cantor（1845—1918）在19世纪后期创立的，之后作为一种基本的数学语言和强有力的研究工具渗透到数学的每一个分支，成为全部数学研究的基础.
所谓集合就是由具有某种性质的个体所组成的一个整体，其中的个体都称之为元素.例如，2025年北京奥运会的所有冠军可以组成一个集合；从北京到上海的全部航班也可以组成一个集合；小于5的自然数也可以组成一个集合，等等.
通常集合用大写字母表示，如A，B，C，P，Q，…；而元素用小写字母表示，如a，b，c，p，q，r，….如果a是集合A的元素，则称为元素a属于集合A，记作a∈A；相反的情况叫作a不属于集合A，记作a∉A或a
A.
由全体自然数组成的集合叫作自然数集合，通常把这个集合记作N.例如，我们有1∈N，23∈N等，但是-1∉N，2.3∉N等.类似地，我们还可以定义整数集合、有理数集合、实数集合、复数集合，这些集合通常记作Z，Q，R，C.
集合的表示方法主要有两种：枚举法和描述法.所谓枚举法，就是写出集合的所有元素，例如：20以下的所有素数集合记作{2，3，5，7，11，13，17，19}；所有完全平方数的集合{1，4，9，16，25，…}；获得过汤姆斯杯冠军的国家的集合{马来西亚，印度尼西亚，中国，日本}等.描述法就是用元素的性质来限定集合中的元素，其表示形式是{x|x具有的性质}.例如：{x|x3-1=0}、{x|3x4-4x2+1≤0}及{x2|x∈N}等.很显然可以看到集合{x2|x∈N}与集合{1，4，9，16，25，…}应该是完全一样的.
集合A可以按其包含的元素是否有限分为有限集合与无限集合，有限集合A的元素个数通常记为|A|.
两个集合之间的基本关系是包含关系.
定义1.1 如果集合A的元素都是集合B的元素，则称集合B包含集合A，或者集合A包含于集合B，记作B⊇A或A⊆B.这时，我们也说集合A是集合B的子集.
这一定义的另一说法是，如果x∈A，那么必然有x∈B.显然，关于数的集合我们有一系列的包含关系：
还有一个特殊的集合称为空集，记作
，空集是不含有任何元素的集合.显然，对任何集合A都有
⊆A.
集合的包含关系有如下性质：
（1）对于任意集合A都有A⊆A；
（2）如果集合A⊆B，B⊆C，则有A⊆C.
证明：这里来证明性质（2）.由包含关系的定义可以知道，我们只需要证明集合A中的元素必然在集合C中就可以了.对任意的元素x∈A，由于A⊆B，因此x∈B.又由于B⊆C，因此x∈C.由定义1.1知道A⊆C.证毕.
定义1.2 若集合A与B互相包含，即有A⊆B与A⊇B同时成立，则称集合A与B相等，记作A=B.
所谓集合B真包含集合A，是指B⊇A但是A≠B，记作B⊃A或A⊂B.这时也称集合A是B的真子集.
集合的运算有交、并、差、对称差和补等.
定义1.3 若A，B是集合，则A，B的交、并、差和对称差的定义和记法依次为
A∩B={x|x∈A且x∈B}，
A∪B={x|x∈A或x∈B}，
A-B={x|x∈A且x∉B}，
A△B=（A-B）∪（B-A）.
当我们考虑一个问题时，所需要考虑的所有元素的集合称为全集.
定义1.4 若I为全集，A是I的子集，则称I-A={x∈I|x∉A}为集合A的补集，记作∁IA或
.
在全集存在的时候，利用补集可以得到差运算的另一表示式：
关于集合的这些运算有如下一些性质：
（1）交换律 A∩B=B∩A，
A∪B=B∪A，
A△B=B△A.
（2）结合律 （A∩B）∩C=A∩（B∩C），
（A∪B）∪C=A∪（B∪C），
（A△B）△C=A△（B△C）.
（3）分配律 （A∩B）∪C=（A∪C）∩（B∪C），
（A∪B）∩C=（A∩C）∪（B∩C）.
（4）幂等律 A∩A=A，
A∪A=A.
（5）0—1律 A∪
=A，
A∩
=
.
（6）吸收律 A∪（A∩B）=A，
A∩（A∪B）=A.
（7）排中律
（8）矛盾律
（9）De Morgan律
(https://www.chuimin.cn)
证明：这里我们证明分配律的第一条和DeMorgan律的第一条，其他的证明留作习题.
证明分配律（A∩B）∪C=（A∪C）∩（B∪C）.由定义1.2可以知道，只需要证明等式两端的集合相互包含，这通常称为证明双包含关系.
首先，证明（A∩B）∪C⊆（A∪C）∩（B∪C）.设x∈（A∩B）∪C，则x∈A∩B或者x∈C.如果x∈A∩B，那么x∈A并且x∈B，因此x∈A∪C并且x∈B∪C.由定义1.3知道x∈（A∪C）∩（B∪C）.如果x∈C，那么x∈A∪C并且x∈B∪C，由定义1.3知道x∈（A∪C）∩（B∪C）.可以看到总有
（A∩B）∪C⊆（A∪C）∩（B∪C）.
其次，证明（A∪C）∩（B∪C）⊆（A∩B）∪C.设x∈（A∪C）∩（B∪C），那么一定有x∈A∪C并且x∈B∪C.如果x∈C，那么显然x∈（A∩B）∪C.如果x∉C，那么必然有x∈A并且x∈B，这时x∈A∩B，因此x∈（A∩B）∪C.可以看到无论如何总有
（A∪C）∩（B∪C）⊆（A∩B）∪C.
综上所述，有分配律（A∩B）∪C=（A∪C）∩（B∪C）成立.
证明De Morgan律
.我们仍然证明双包含关系.
首先，证明
设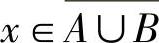
，则x∉A∪B，这表明x∉A并且x∉B，也即x∈A并且x∈B.于是有x∈A∩B.因此，A∪B⊆A∩B.
其次，证明
设
，那么
并且
，即x∉A并且x∉B，因此x∉A∪B，即
于是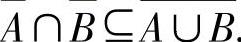
综上所述，有DeMorgan律A
B成立.
证毕.
例1.1 化简集合表达式（（A∪B∪C）∩（A∪B））-（（A∪（B-C））∩A）.
解：
其中，第一个等号使用的是吸收律；第二、六个等号使用的是差运算的第二种形式；第三个等号利用的是分配律；第四个等号用矛盾律；第五个等号用0-1律.
例1.2 已知集合A，B，X满足等式
A∪B∪X=A∪B，
A∩X=B∩X=A∩B.
证明：X=A∩B.
证明：
X=（A∪B∪X）∩X
=（A∪B）∩X
=（A∩X）∪（B∩X）
=（A∩B）∪（A∩B）
=A∩B.
其中，第一个等号使用吸收律；第二、四个等号使用已知条件；第三个等号使用分配律；第五个等号使用幂等律.
定义1.5 若集合A，B都是非空集合，那么集合
{（a，b）|a∈A，b∈B}
称为集合A与B的笛卡儿积，记作A×B.
一般来说，A×B≠B×A.类似地，还可以定义n个非空集合Ai的笛卡儿积A1×A2×…×An.
习题
1.1.1. 设A，B是两个集合，A⊆B且A∈B可能吗？
1.1.2. 化简集合表达式：（A-B-C）∪（（A-B）∩C）∪（A∩B-C）∪（A∩B∩C）.
1.1.3. 证明：A⊆A∪B，A∩B⊆A.
1.1.4. 证明：A⊆B当且仅当A∪B=B.
1.1.5. 证明：A⊆B当且仅当A∩B=A.
1.1.6. 证明：（A-B）-C=（A-C）-（B-C）.
1.1.7. 已知：A∩C⊆B∩C，A-C⊆B-C，证明：A⊆B.
1.1.8. 证明：A△A=
，A△
=A.
1.1.9. 证明：对任何集合A，B，C，都有A△B⊆（A△C）∪（B△C）.
1.1.10. 证明：对两个集合X，Y，X=
当且仅当Y=X△Y.
1.1.11. 若A△B=A△C，那么B=C.
相关文章
- 详细阅读
-
使用forEach迭代数组，获取运算结果详细阅读
循环获取数组元素进行运算是很常见的操作，数组具有length属性，因此往往会使用for i++形式对数组进行迭代。in迭代数组使用typeof检测数组，返回"object"，表明数组也属于对象，可以使用for…in语句会自动跳过该索引，for i++则不会跳过。◇ thisArg：可选参数，表示执行callback时绑定的this对象。动手写9.4.12执行9.4.12.html，输出结果到网页，如下图所示。图9.4.12使用forEach()迭代数组......
2025-09-30
-
微分运算法则-高等数学上册详细阅读
由函数的和、差、积、商的求导法则，结合公式（2－46）可推得相应的微分运算法则，为了便于对照，列于表2－2中.表2－2函数的求导法则与微分法则下面仅以乘积的微分法则为例加以证明.由函数微分公式（2－46），有d（uv）＝（uv）′dx＝（u′v＋uv′）dx＝u′dx·v＋u·v′dx＝vdu＋udv因此d（uv）＝vdu＋udv其他法则均可类似证明.请读者自证.下面讨论复合函数的微分.设函数y......
2025-09-30
-
极限运算法则-高等数学详细阅读
一、四则运算法则定理1.9 若，，则1）；2）；3）当b≠0时，.证 只证2）.因为，存在δ0>0，当0＜|x-x0|＜δ0时，|f（x）|≤M.对于任意给定的ε＞0，存在δ1＞0，当0＜|x-x0|＜δ1时，有f（x）-a＜ε成立；对于任意给定的ε＞0，存在δ2＞0，当0＜|x-x0|＜δ2时，有g（x）-b＜ε成立；取δ=min{δ0，δ1，δ2}，则当0＜|x-x0|＜δ时，有|f（x）·g......
2025-09-30
-
高等数学上册：连续函数运算法则详细阅读
1）连续函数的四则运算法则函数的连续性是由函数的极限来定义的，所以根据极限的四则运算法则，可得下面的连续函数的四则运算法则.定理1若函数f（x）与g（x）都在点x0处连续，则函数f（x）±g（x），f（x）·g（x）都在点x0处连续，若再增加条件g（x0）≠0，则也在点x0处连续.证设函数f（x），g（x）都在点x0处连续，所以由极限的加、减、乘运算法则，可得即f（x）±g（x），f（x）·g......
2025-09-30
-
加权代数连通度的定义与计算详细阅读
图5-1给出的例子中包括了5个节点组成的不同拓扑的网络结构及其对应的代数连通度。图5-1代数连通度概念示例λ2=0；λ2=0.382 0；λ2=1.382 0；λ2=5代数连通度的最大化问题是图论中一个经典的数学规划问题。在星间组网系统中，考虑到星上资源受限，本章在代数连通度的概念基础上增加了链路权重的因素，将代数连通度扩展为加权代数连通度加以分析。以权重矩阵来计算加权代数连通度的方法与以邻接矩阵来计算非加权代数连通度的方法相同。......
2025-09-29
-
张宇线性代数9讲：求解A矩阵详细阅读
，αm，βT线性无关.例5.16 已知齐次线性方程组A2×4x＝0的基础解系为ξ1＝［1，－1，3，2］T，ξ2＝［2，1，1，－3］T，则A＝________.应填，其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.由题设条件知，Aξ1＝0，Aξ2＝0，即两边转置，得作齐次线性方程组对系数矩阵作初等行变换，有取y2＝0，y3＝k，得，则解向量为取y2＝l，y3＝0，得，则解向量为其中k1，l1，k2，l2 是不全为零的常数，且k1l2≠k2l1.......
2025-09-30
-
线性代数习题解法+例题讲解详细阅读
，s）均可逆，则A可逆，且见例3.16.例3.12 已知，写出A可逆的一个充要条件，当A可逆时，求A－1.A可逆故当ad－bc≠0时，例3.13 设n阶方阵A 满足A3－2A2＋3A－4E＝O，则A－1＝________.若能找到n阶方阵B，使得AB＝E，则A－1＝B.这样的B应利用题设条件去找.应填由题设条件A3－2A2＋3A－4E＝O，移项得A3－2A2＋3A＝4E，左端提出公因子，得 A＝4E，即故知A可逆，且类似本题的一般问法：设f是多项式，且f＝akxk＋ak－1xk－1＋…......
2025-09-30
相关推荐