首页理论教育机电应用数学：椭圆的标准方程与定义

机电应用数学：椭圆的标准方程与定义

2023-11-22 理论教育版权反馈

【摘要】：1.椭圆的定义做一做取一条一定长的细绳，把它的两端固定在画图板上的F1和F2两点，当绳长大于F1和F2的距离时，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动，请同学们利用手中绳子配合同桌共同完成，看看可以得到什么图形.图4-18议一议在画图的过程中，哪些量发生了变化？

观察与思考

在自然界、科学界、技术界乃至我们的生活中都存在大量的“椭圆”形态，如嫦娥二号卫星的绕月飞行轨迹、行星运行轨迹、国家大剧院、国家体育场“鸟巢”、油罐车等.那么，椭圆是怎样定义的呢？它的标准方程又是什么呢？

1.椭圆的定义

做一做

取一条一定长的细绳，把它的两端固定在画图板上的F₁和F₂两点（见图4-18），当绳长大于F₁和F₂的距离时，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动，请同学们利用手中绳子配合同桌共同完成，看看可以得到什么图形.

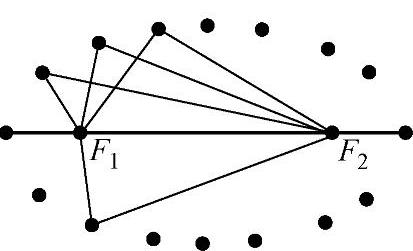
图4-18

议一议

在画图的过程中，哪些量发生了变化？哪些量没有变？

根据实验结果，可以看到：“两定点间的距离没变，绳子的长度没变，而点在运动.”所以，椭圆是由与点F₁和F₂的距离的和等于这条绳长的点组成.

平面上到两个定点F₁，F₂的距离之和为定长（大于F₁F₂）的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点，两焦点的距离叫做焦距.

2.椭圆的标准方程

根据椭圆的定义，来求椭圆的标准方程.

过焦点F₁，F₂的直线为x轴，线段F₁F₂的垂直平分线为y轴，建立直角坐标系.如图4-19a所示.

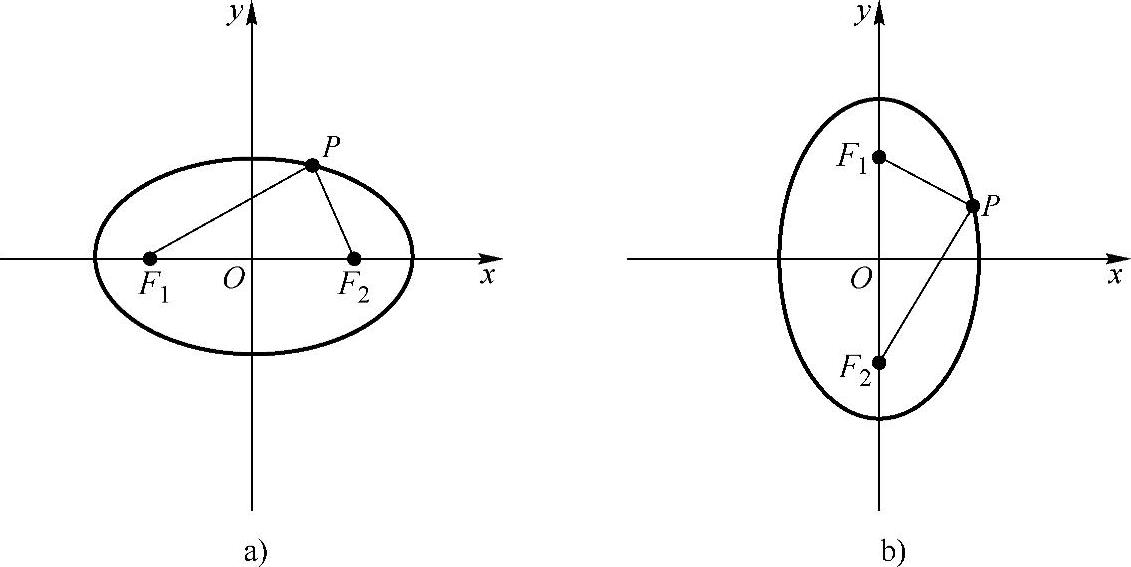
图4-19

设P（x，y）是椭圆上任意一点，椭圆的焦距F₁F₂=2c（c>0），则F₁，F₂的坐标分别是（-c，0），（c，0）.P与F₁和F₂的距离的和为固定值2a（2a>2c）.

根据椭圆的定义，找出动点P满足的条件，即

PF₁+PF₂=2a

由，，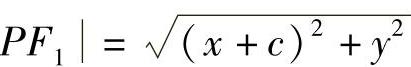

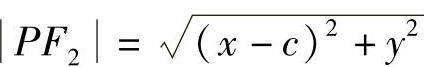得到

下面看看怎样化简？

一般来说：

1）方程中只有一个二次根式时，需将它单独留在方程的一边，把其他各项移到另一边，平方一次；

2）方程中有两个二次根式时，需将它们分散，放在方程的两边，使其中一边只有一个根式，平方两次.

于是就有了结果

但这个方程还不够简洁对称，再观察图形：

从图中找出表示a，c，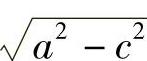

的线段，令b²=a²-c²，

从而将方程简化为

称此方程为椭圆的标准方程.它所表示的椭圆的焦点在x轴上，焦点是F₁（-c，0），F₂（c，0），这里c²=a²-_b².

如果椭圆的焦点在y轴上，焦点是F₁（0，-c），F₂（0，c）（见图4-19b），只要将方程（1）的x，y互换，就可以得到它的方程，这时方程为

(www.chuimin.cn)

例1　判断下列各椭圆的焦点位置，并求出焦点坐标、焦距及a、b的值.

分析：从椭圆的标准方程不难看出椭圆的焦点位置可由方程中含字母x²，y²项的分母的大小来确定，分母大的项对应的字母所在的轴就是焦点所在的轴.

解：（1）从方程形式可以看出a²=4，b²=3，进而，a=2，b=3，c²=a²-b²=4-3=1，c=1.

焦点在y轴上，焦点坐标（0，-1），（0，1），焦距为2.

（2）先将原方程化为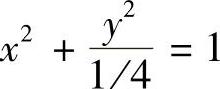：，由此可以看出，此椭圆焦点在x轴上，a²=1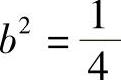，，进而a=1，，，

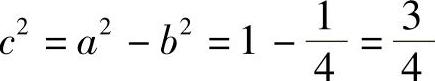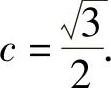
焦点坐标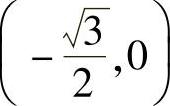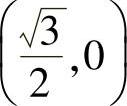，，焦距为

（3）分析方程形式，可以看出，a²=4，b²=1，进而a=2，b=1，c²=a²-b²=4-1=3，焦点在y轴上，焦点坐标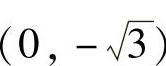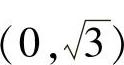，，焦距为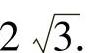

例2　已知椭圆两个焦点的坐标分别为（-4，0），（4，0），椭圆上一点P到两焦点距离的和等于10，求椭圆的标准方程.

解：因为椭圆的焦点在x轴上，所以设椭圆的标准方程为

因为c=4，2a=10，所以a=5，b²=a²-c²=5²-4²=9，b=3.

所以椭圆的标准方程为

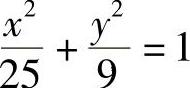
例3 图4-20为含椭圆形的零件加工图样，其中椭圆方程为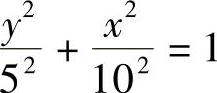，求点T的

坐标.

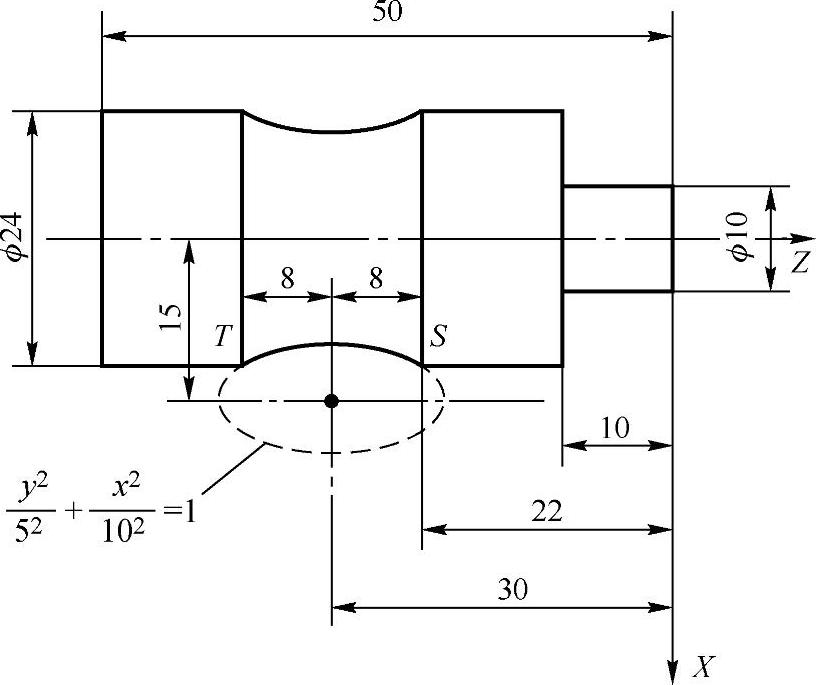
图4-20

解：由图可知，点T的横坐标为-8，代入椭圆方程得

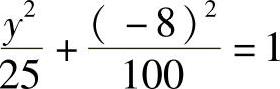
所以y=±3，点T的坐标为（-8，3）.

练习

1.判断下列各椭圆的焦点位置，并求出焦点坐标和焦距.

（1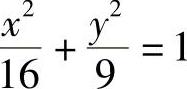）；（2）9x²+y²=81；（3）2x²=1-_y².

2.求满足下列条件的椭圆的标准方程：

（1）a=6，b=3；（2）a=5，；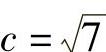

（3），焦距是6.

习题五

1.根据下列条件，求椭圆的标准方程：

（1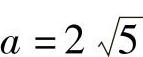），经过点A（2，-3），焦点在y轴上；

（2）焦点坐标是（-6，0），（6，0），

2.求椭圆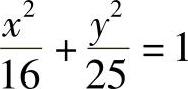上一点M（2.4，4）与焦点的距离.

3.已知椭圆经过点A（x，2），求x的值.

4.已知椭圆的焦点在x轴上，并且经过点（5，0），（0，-4），求它的标准方程.