首页理论教育两点间距离和中点坐标的公式

两点间距离和中点坐标的公式

2023-11-22 理论教育版权反馈

【摘要】：观察与思考在平面直角坐标系中，任何一点P都可以用有序实数对（x，y）表示，我们把（x，y）叫做点P的坐标，记作P（x，y）.如果给出了两个点的坐标，应如何计算这两点间的距离并确定这两个点的中点位置呢？

观察与思考

在平面直角坐标系中，任何一点P都可以用有序实数对（x，y）表示，我们把（x，y）叫做点P的坐标，记作P（x，y）.如果给出了两个点的坐标，应如何计算这两点间的距离并确定这两个点的中点位置呢？

下面学习两个常用的公式，即两点间距离公式和中点坐标公式.

1.两点间距离公式

先看两点都在x轴上的情况（见图4-6）：

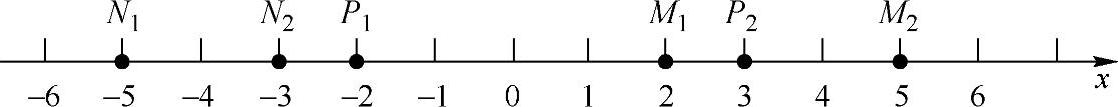
图4-6

从图4-6可以直观地看出：

M₁与M₂的距离M₁M₂=5-2=3；

N₁与N₂的距离N₁N₂=-3-（-5）=2；

P₁与P₂的距离P₁P₂=3-（-2）=5.

一般地，如果x轴上的两点M₁与M₂的坐标分别为x₁，x₂，那么M₁与M₂的距离为

M₁M₂=x₂-x₁

即x轴上的两点间距离是这两点坐标差的绝对值.同样，y轴上的两点间距离也是它们两点坐标差的绝对值.

如果P₁（x₁，y₁）P₂（x₂，y₂）是坐标平面上的任意两点，那么它们的距离又该如何计算呢？

如图4-7所示，平面直角坐标系内任意两点间的距离公式：

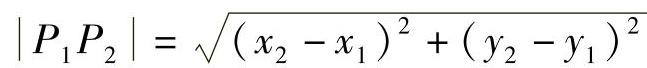
例1　计算M₁（2，-5），M₂（5，-1）两点间距离.

解：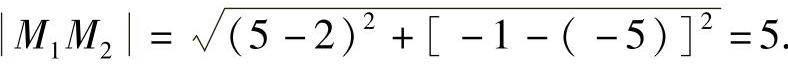

即M₁，M₂两点间的距离为5.

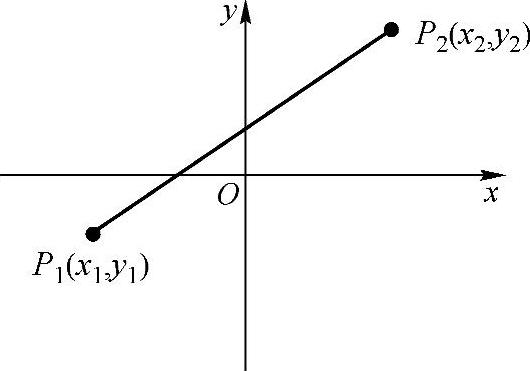
图4-7

练一练

求下列两点间距离：（1）A₁（0，8），A₂（6，0）；

（2）B₁（5，12），B₂（-3，4）.

2.中点坐标公式

如图4-8所示，设P₁（x₁，y₁），P₂（x₂，y₂）为平面直角坐标系内的任意两点，P（x，y）为

线段P₁P₂的中点，则

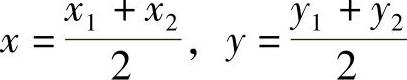
例2　求下列两点的线段的中点坐标：(www.chuimin.cn)

（1）P₁（8，-3），P₂（-4，7）；

（2）A（4，0），B（0，6）.

解：（1）根据中点坐标公式得

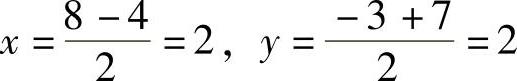
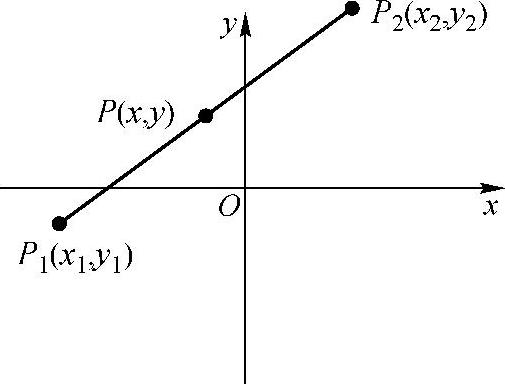
图4-8

所以线段P₁P₂的中点坐标是（2，2）.

（2）根据中点坐标公式得

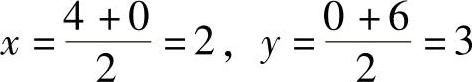
所以线段AB的中点坐标是（2，3）.

例3 如图4-9所示，已知A（-1，0），B（3，-1），C（5，2），求三角形ABC在AC边上的中线长.

解：设D（x，y）是AC边上的中点，根据中点坐标公式

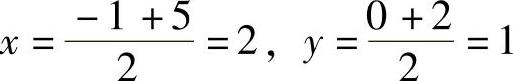
即点D的坐标是（2，1）.

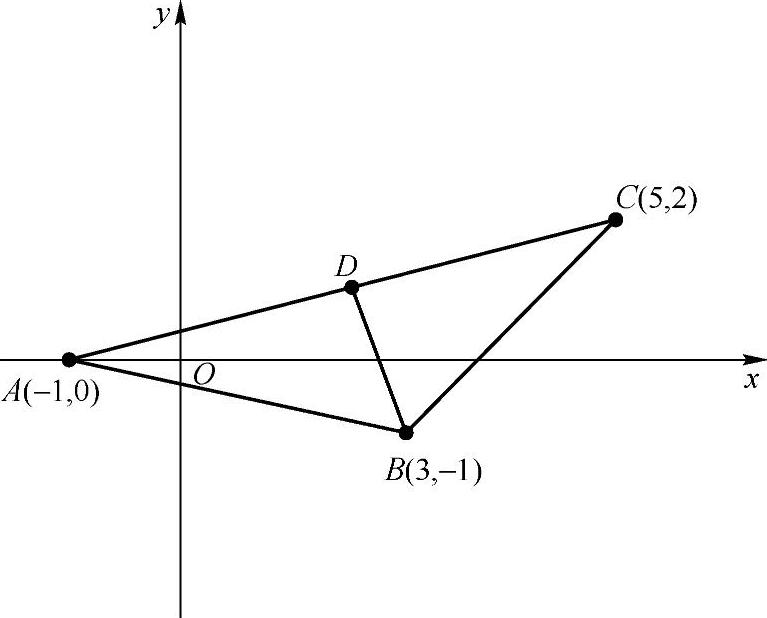
图4-9

再由两点间距离公式，得

即三角形ABC中AC边上的中线长为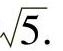

练习

1.数轴上点A的坐标是3，点B的坐标是-5，则AB=.

2.求连接下列两点间的距离及其中点坐标：

（1）A（-6，-8），B（0，0）；（2）C（0，-3），D（-4，0）；

（3）M（4，7），N（-1，2）；（4）E（10，8），F（6，4）.

习题二

1.已知点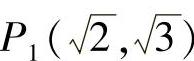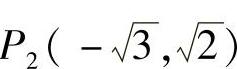，，求P₁P2.

2.求点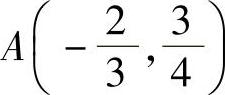，B（3，-4）的中点坐标.

3.已知点C是线段AB的中点，点C（-1，2），点A（4，5），求点B的坐标.

4.三角形的三个顶点是A（-2，-1），B（2，3），C（1，1），求AB边上中线的长度.