首页理论教育多面体的体积计算方法及应用

多面体的体积计算方法及应用

2023-11-22 理论教育版权反馈

【摘要】：2.已知一个正三棱柱的底面边长为3，高为4，求这个正三棱柱的体积.3.已知正四棱锥的底面边长为4，高为3.求这个正四棱锥的体积.4.旋转体的体积圆柱与棱柱的体积计算方法类似，都等于它的底面积S和高h的乘积，即V圆柱=Sh圆锥的体积也是同底等高的圆柱体积的，即其中，S是底面面积；h是圆锥的高.例4 有一堆相同规格的六角螺母毛坯，共重5.8kg.已知螺母的底面六边形边长是12mm，高是10mm，内孔直径是10mm，问约有毛坯多少个？

棱柱的体积公式与正方体、长方体体积公式一致，可以统一为

V_棱柱=Sh

其中，S是底面面积；h是棱柱的高.

棱锥的体积是同底等高的棱柱体积的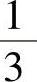，即棱锥的体积为

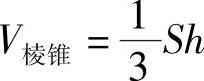
其中，S是底面面积；h是棱锥的高.

例3　如图3-63所示，在长方体ABCD—A′B′C′D′中，用截面截下一个棱锥C—A′DD′，求棱锥C—A′DD′的体积与剩余部分的体积之比.

解：已知长方体可以看成直四棱柱ADD′A′—BCC′B′，设它的底面ADD′A′面积为S，高为h，则它的体积为

V=Sh

因为棱锥C-A′DD′的底面面积为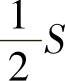，高是h，所以

棱锥C-A′DD′的体积

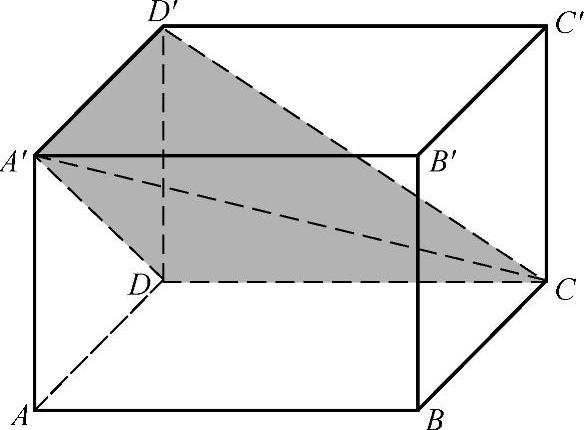
图3-63

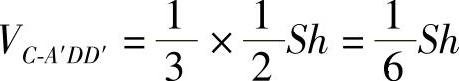
图3-63中余下部分的体积是

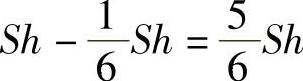
所以棱锥C-A′DD′的体积与剩余部分的体积之比为1∶5.

练习

1.在正方体ABCD—A′B′C′D′中，三棱锥A′-BC′D的体积是正方体体积的几分之几？

2.已知一个正三棱柱的底面边长为3，高为4，求这个正三棱柱的体积.

3.已知正四棱锥的底面边长为4，高为3.求这个正四棱锥的体积.

4.旋转体的体积

圆柱与棱柱的体积计算方法类似，都等于它的底面积S和高h的乘积，即V_圆柱=Sh

圆锥的体积也是同底等高的圆柱体积的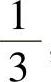，即

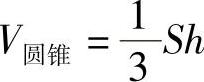
其中，S是底面面积；h是圆锥的高.

例4 有一堆相同规格的六角螺母毛坯（见图3-64），共重5.8kg.已知螺母的底面六边形边长是12mm，高是10mm，内孔直径是10mm，问约有毛坯多少个（铁的密度是7.8g/cm³，π≈3.14）？

解：六角螺母毛坯的体积是一个正六棱柱的体积和一个圆柱的体积的差.

因为，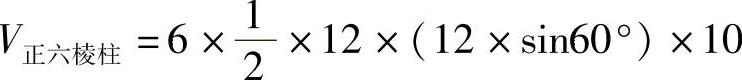

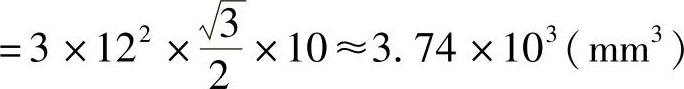V_圆柱=3.14×（10÷2）2×10≈0.785×10³（mm³），

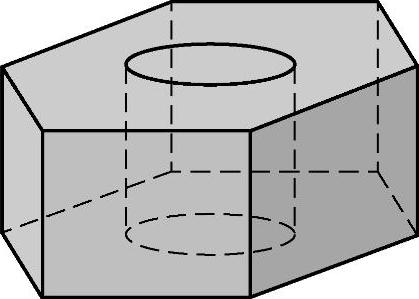
图3-64

所以，毛坯的体积

V=3.74×10³-0.785×10³

≈2.956×10³（mm³）

=2.956（cm³）(www.chuimin.cn)

5.8×10³÷（7.8×2.956）≈251（个）

即这堆毛坯约有251个.

如果球的半径为R，那么它的体积为

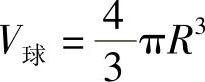
例5　一种空心钢球的质量是142g，外径是5.0cm求它的内径（钢的密度是7.9g/cm³）.

解：设空心钢球的内径为2x（cm），那么钢球的质量是

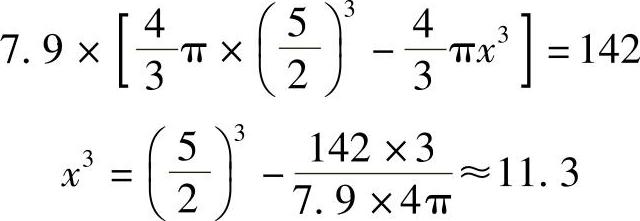
所以x≈2.24，

2x≈4.5（cm）.

即空心钢球的内径约为4.5cm.

练习

1.一个圆柱的底面半径为4，母线长为5，求这个圆柱的体积.

2.已知圆锥的母线长为5cm，高为3cm，求这个圆锥的体积.

3.有一个正方体，内接于半径为R的球内，求正方体的体积.

习题五

1.选择题.

（1）棱长都是1的三棱锥的表面积为（）.

（2）等边三角形边长为4，它绕其一边所在的直线旋转一周，则所得旋转体的体积是（）.

A.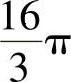

B.8π　C.12π　D.16π

（3）若两个正方体的体积之比是1∶8，那么这两个正方体的表面积之比为（）.

A.1∶2　B.1∶4　C.1∶6　D.1∶8

（4）圆柱的轴截面（过轴的截面）是边长为2的正方形，则其侧面积为（）.

A.π　B.2π　C.4π　D.8π

2.填空题.

（1）已知一个长方体的长、宽、高分别为12，4，3，则长方体的对角线长为，表面积为，体积为.

（2）若三个球的表面积之比是1∶2∶3，则它们的体积之比是.

（3）一个正四棱锥的高是a，底面边长是2a，则它的表面积为，体积为.

（4）已知圆柱的一个底面积为4π，母线长为3，则圆柱的表面积为，体积为.

3.如习题图3-25所示，现有一长方体盒子ABCD—A₁B₁CD₁，AB=3，BC=2，AA₁=1，一根绳子从点A沿着表面拉到点C₁的最短距离为多少？请找一个长方体的盒子及一根细绳尝试不同的测量方法，

从中找出最短的距离.

4.已知长方体形的铜块长、宽、高分别是2，4，8，将它熔化后铸成一个正方体的铜块（不计损耗），求铸成铜块的棱长.

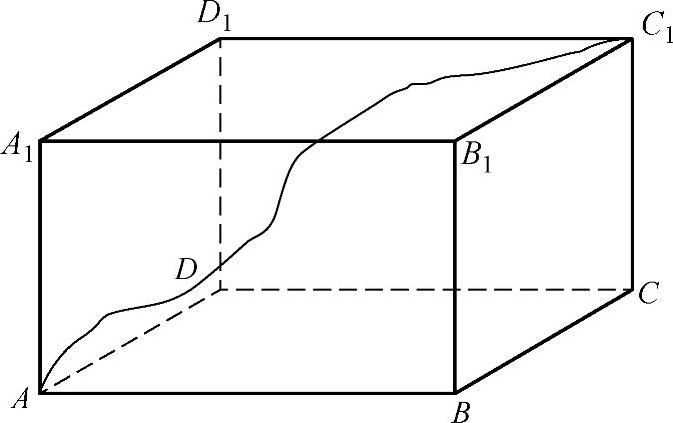
习题图3-25