机电应用数学：多面体表面积的计算方法与展开图关系

2023-11-22 理论教育版权反馈

【摘要】：想一想我们过去学习过的正方体和长方体的表面积如何求？并说一说它们的展开图与它们的表面积有怎样的关系呢？试画出它的展开图.图3-60如何计算它的表面积？

想一想

我们过去学习过的正方体和长方体的表面积如何求？请画出它们的展开图？并说一说它们的展开图与它们的表面积有怎样的关系呢？

正方体和长方体是由多个平面图形围成的多面体，它们的表面积就是各个面的面积之和，也就是展开图的表面积（见图3-58）.

图3-58

试一试　把正六棱柱展开，并画出它的展开图（见图3-59）.

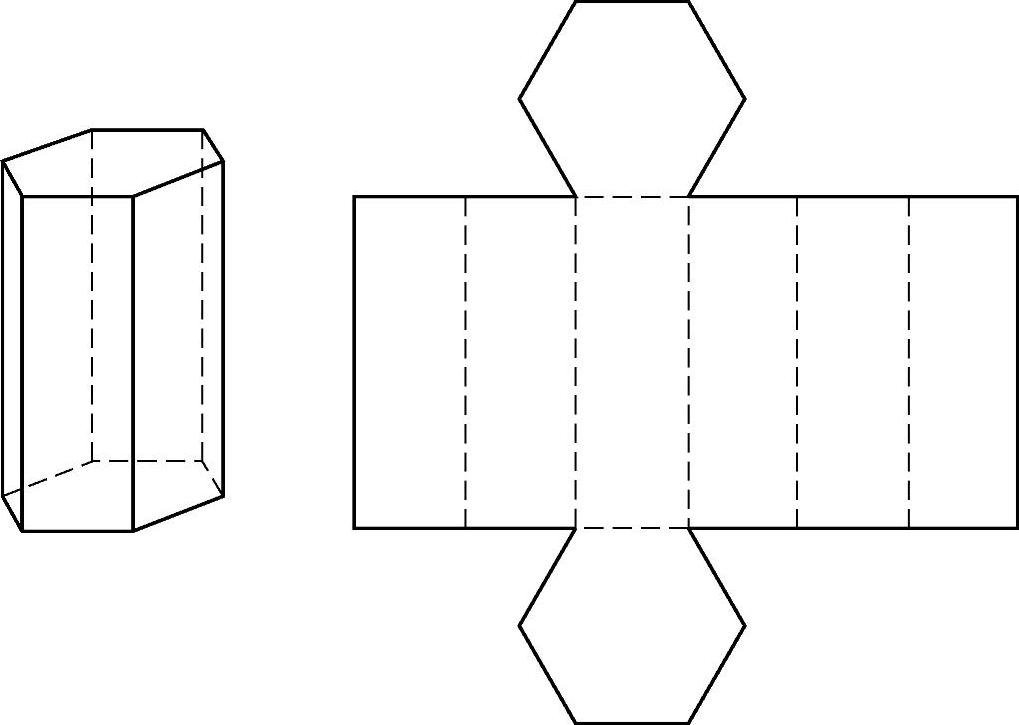
图3-59

直棱柱的侧面展开图是一个矩形.这个矩形的边长等于直棱柱底面的周长，另一边长等于侧棱长.

设直棱柱的底面多边形的周长为c，侧棱长为h，则直棱柱的侧面积是

S_直棱柱侧=ch

我们也可以得到直棱柱的表面积计算公式

S_直棱柱表=2S_直棱柱底+S_直棱柱侧

试一试　正四棱锥的展开图是由哪些图形组成的？试画出它的展开图（见图3-60）.

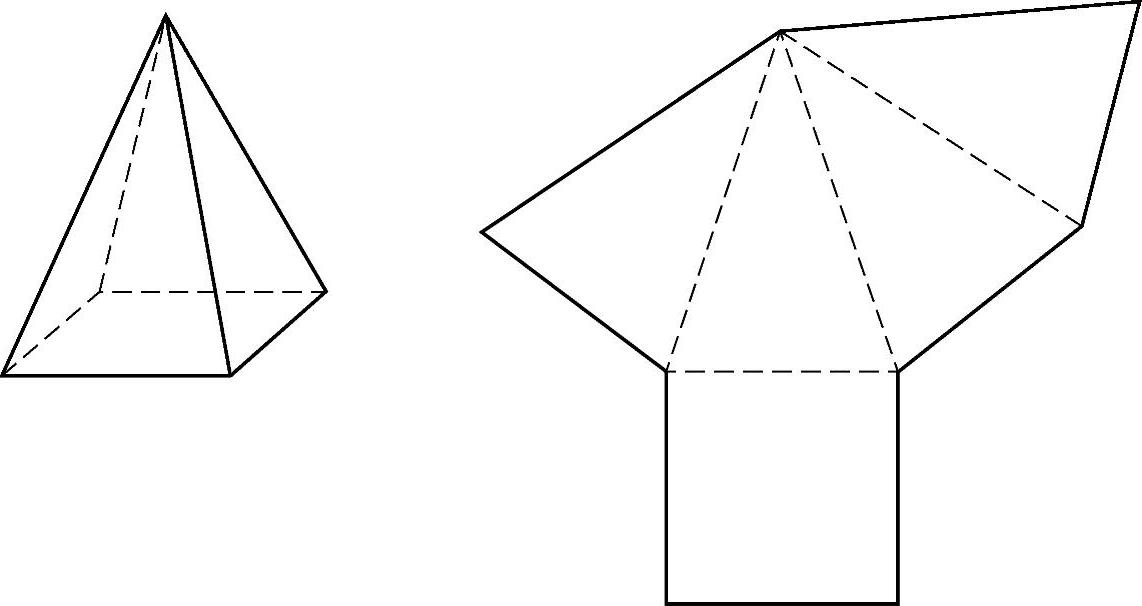
图3-60(www.chuimin.cn)

如何计算它的表面积？

正棱锥的表面积等于它的侧面积与底面正多边形的面积之和，即

其中，c为底面正多边形的周长；h′为斜高.

例1　已知正四棱锥底面正方形的边长为4cm，高与斜高的夹角为30°，求正四棱锥的侧面积及表面积.

解：正棱锥的高、斜高、底面边心距组成Rt△OPE.

因为OE=2cm，∠OPE=35°，

所以斜高

因此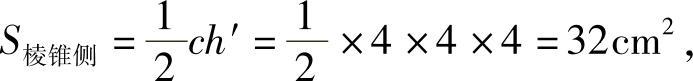

S_正棱锥表=32+16=48cm2.

练习

1.已知一个正三棱柱的底面边长为3，高为4，求这个正三棱柱的侧面积和表面积.

2.以一张长和宽分别为8cm和6cm的矩形硬纸板为侧面，将它折成正四棱柱，求该四棱柱的对角线的长.

3.一个正四棱锥S—ABCD的高SO和底边边长都是4，求它的表面积.