在实际的生产和生活中，我们经常遇到的并不是简单的几何体，而是由一些简单几何体构成的组合体.对于组合体，一定要认真观察，先弄清楚它的基本结构，然后再画它的三视图.试一试如图3-51所示的组合体，它是由哪些简单几何体组合而成的？你能画出它的三视图吗？......
2023-11-22
三视图在机电应用数学中的重要性
【摘要】：在立体几何中，为了使空间图形的直观图能够更准确地反映空间图形的大小和形状，往往需要把图形向几个不同的平面分别作正投影，然后把这些投影图放在同一个平面内，并有机地结合起来表示物体的形状和大小.用正投影绘制物体的图形，叫做视图.但一面视图不能完全确定物体的形状和大小.如图3-48所示的三个不同形状的物体在一个投影面上的投影都是相同的.图3-48通常，总是选取三个两两互相垂直的平面作为投影面（见图3-4
在立体几何中，为了使空间图形的直观图能够更准确地反映空间图形的大小和形状，往往需要把图形向几个不同的平面分别作正投影，然后把这些投影图放在同一个平面内，并有机地结合起来表示物体的形状和大小.
用正投影绘制物体的图形，叫做视图.但一面视图不能完全确定物体的形状和大小.如图3-48所示的三个不同形状的物体在一个投影面上的投影都是相同的.
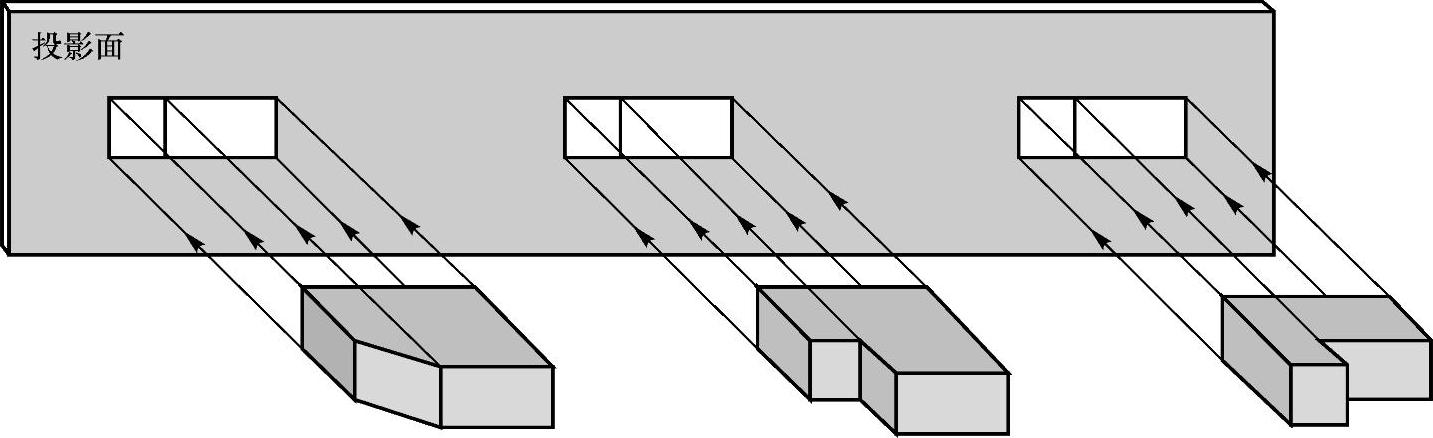
图3-48
通常，总是选取三个两两互相垂直的平面作为投影面（见图3-49）.一个投影面水平放置，叫做水平投影面（简称水平面），几何体投射到这个平面内的图形叫做俯视图；一个投影面放置在正前方，这个投影面叫做正立投影面（简称正面），几何体投射到这个面内的图形叫做主视图；和正立、水平两个投影面都垂直的投影面叫做侧立投影面（简称侧面），通常把这个平面放在正立投影面的右侧，投射到这个平面内的图形叫做左视图.
将空间图形向这三个平面作正投影，然后把这三个投影按一定的布局放在一个平面内，这样构成的图形叫做空间图形的三视图.
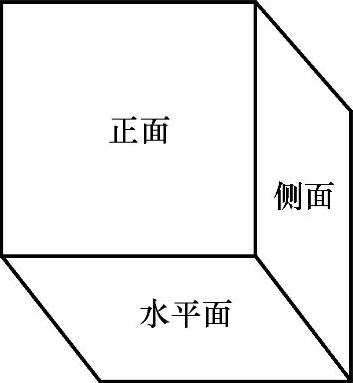
图3-49
图3-50是一个长方体的三视图.长方体的侧面分别平行于三个投影面，把它向三个投影面投影：(www.chuimin.cn)
它的主视图是一个矩形，它表示长方体的长度（a）和高度（c）；
它的俯视图也是一个矩形，它表示长方体的长度（a）和宽度（b）；
它的左视图仍然是一个矩形，它表示长方体的宽度（b）和高度（c）.
任意一个物体的长、宽、高，一般指的是物体占有空间的左右、前后、上下的最大距离.一个物体的三视图的排列规则是，俯视图在主视图的下面，长度与主视图一样，左视图放在主视图的右面，高度与主视图一样，宽度与俯视图一样.这个三视图之间的规律，也称为“三等”规律，即主、俯视图“长对正”（等长）；主、左视图“高平齐”（等高）；俯、左视图“宽相等”（等宽）.
在画三视图时，看得见部分的轮廓线要画成实线，看不见部分的轮廓线要画成虚线.
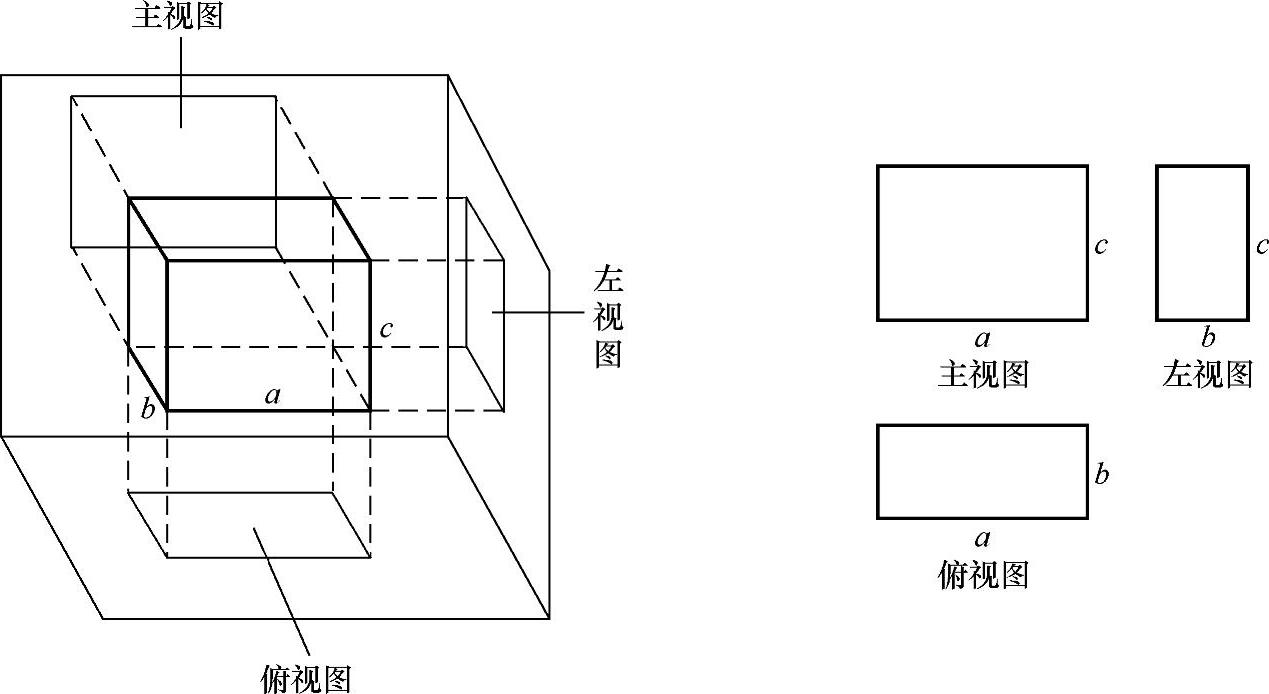
图3-50
有关机电应用数学的文章
- 详细阅读
-
投影现象及其应用-机电应用数学详细阅读
我们知道，光是沿直线传播的.物体在光线的照射下，会在不透明物体后面的屏幕上（如墙面或地面等）留下这个物体的影子（见图3-39），这种现象就叫做投影.其中，把光线叫做投影线，把留下物体影子的屏幕叫做投影面.图3-39（1）中心投影把光由一点向外散射所形成的投影，叫做中心投影（见图3-40）.中心投影的投影线交于一点，即投射中心.中心投影现象普遍存在于我们的生活中.例如，舞台灯、路灯、手电筒和台灯的光......
2023-11-22
- 详细阅读
-
机电应用数学：椭圆的标准方程与定义详细阅读
1.椭圆的定义做一做取一条一定长的细绳，把它的两端固定在画图板上的F1和F2两点，当绳长大于F1和F2的距离时，用铅笔尖把绳子拉紧，使笔尖在图板上慢慢移动，请同学们利用手中绳子配合同桌共同完成，看看可以得到什么图形.图4-18议一议在画图的过程中，哪些量发生了变化？......
2023-11-22
- 详细阅读
-
机电应用数学：数的认识与区别详细阅读
回顾与思考初中学过的数，它们的关系可以归纳如下：议一议有理数和无理数有什么区别？数的集合简称数集，全体非负整数的集合，通常简称非负整数集，记作N，非负整数集内排除0的集合，也称正整数，记作N+；全体有理数的集合，简称有理数集，用Q表示；全体实数的集合，简称实数集，用R表示.为了方便，还用Q+表示正有理数集，Q-表示负有理数集；R+表示正实数集，R-表示负实数集.我们通常用大写拉丁字母A，B，C，…......
2023-11-22
-
高考数学应用题：导数在函数中的应用详细阅读
续表考点：导数在研究函数中的应用（2017全国I，21）已知函数f（x）=ae2x+（a-2）ex-x.（1）讨论f（x）的单调性；（2）若f（x）有两个零点，求a的取值范围.1.（2017山东莱芜二模）已知函数f（x）=ex[x2+（a+1）x+2a-1].（1）当a=-1时，求函数f（x）的单调区间；（2）若关于x的不等式f（x）≤ea在[a，+∞）上有解，求实数a的取值范围；（3）若曲线y=......
2023-10-15
-
正弦函数性质及解析-机电应用数学详细阅读
由正弦函数y=sinx的图像可知：定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx，x∈R的值域是[-1，1]，即对任意的x∈R，都有-1≤sinx≤1.其中，当，k∈Z，有ymax=1；当，k∈Z时，有ymin=-1.想一想等式2sinx=3，，都成立吗？例2求出下列函数的最大值和最小值：y=1-sinx； y=2sinx.解：当sinx=-1时，ymax=1-（-1）=2；当sinx=1时，ymin=1-1=0.当sinx=1时，ymax=2×1=2；sinx=-1时，ymin=2×（-1）=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时，对应的x的取值集合分别是什么？......
2023-11-22
相关推荐