(一)相对性我们生活的周围空间是向纵、横、深三个方向扩展的,空间坐标系按照纵、横、深三个扩展方向形成的三对相对应的基本方向,分别表示为前后、左右和上下三对方向的位置。图10-2以小刚为参照物(三)连续性空间方位的连续性指的是空间方位从上到下、从前到后、从左到右等的区域是连续的,不能截然分开。可变性、相对性和连续性所反映的物体空间位置关系的基本特性是一致的。......
2025-09-29
在现实世界中,存在着各种各样的物体,它们都占据着一定的空间.如果只考虑这些物体的大小和形状,而不考虑其他因素,那么由这些物体抽象出来的空间图形就叫做空间几何体.
观察与思考
仔细观察下面的图片(图3-22a、b),你能说出它们都是什么建筑吗?它们都具有怎样的形状?它们的轮廓抽象出的是什么图形?

图3-22
它们分别是中国国家游泳中心“水立方”以及法国卢浮宫前的“玻璃金字塔”.它们的轮廓抽象出的图形如图3-23a、b所示.
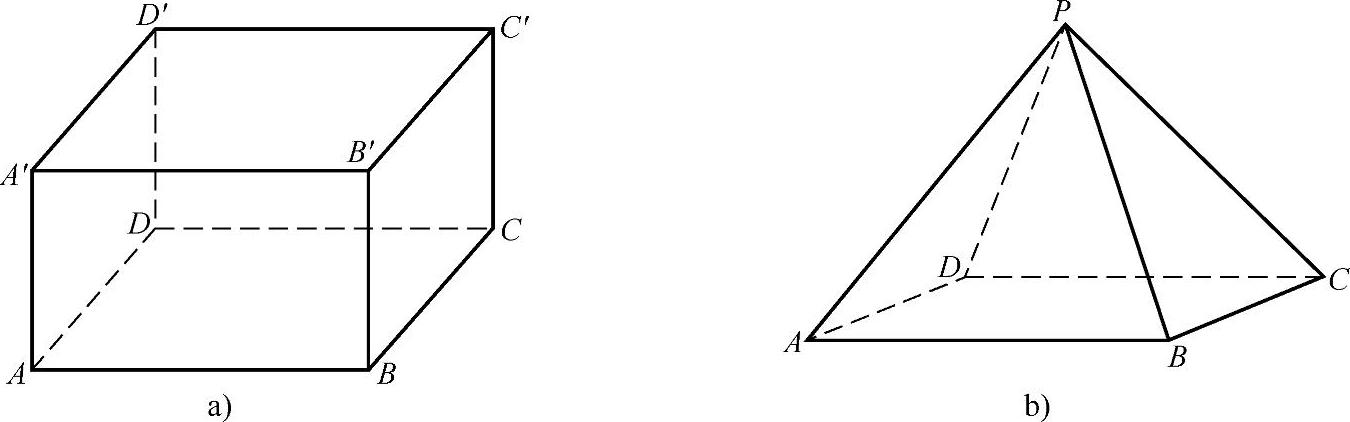
图3-23
1.多面体的结构特征
这些空间几何体具有相同的特点:组成几何体的每个面都是平面图形,并且是平面多边形(包括它们内部的平面部分).
一般地,我们把由若干个平面多边形围成的几何体叫做多面体.图3-23中的几何体都是多面体.
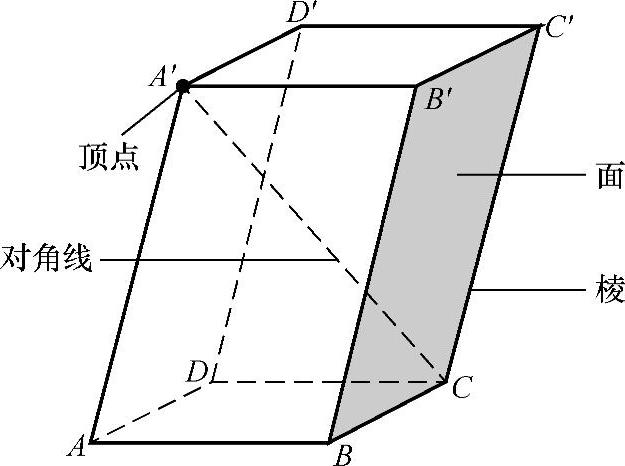
图3-24
如图3-24所示,围成多面体的各个多边形叫做这个多面体的面,如面ABCD、面BCC′B′;相邻的两个面的公共边叫做多面体的棱,如棱AB、棱CC′;棱和棱的公共点叫做多面体顶点,如顶点A′,C;连接不在同一面上的两个顶点的线段叫做多面体的对角线,如对角线A′C.
一个多面体至少有四个面,多面体依照它的面数分别叫做四面体、五面体、六面体等.
试一试
任意画一个四面体和六面体,分别数一数它们各有多少条棱,多少条对角线,多少个顶点.
棱柱和棱锥是最常见也是最简单的多面体,在生产和生活中都有着广泛的应用,下面我们将分别介绍它们的结构特征.
(1)棱柱的结构特征
观察与思考
三棱镜、孔明灯、首饰盒(见图3-25a~c)都是我们生活中常见的物体,认真观察它们的形状,说说它们具有什么样的共同特征?

图3-25
通过观察图3-25,我们发现这些多面体都有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱.棱柱中互相平行的两个面叫做棱柱的底面,简称底;其余的各面叫做棱柱的侧面;相邻两侧面的公共边叫做棱柱的侧棱;侧棱与底面的公共点叫做棱柱的顶点;不在同一个面上的两个顶点的连线叫做棱柱的对角线;两个底面间的距离叫做棱柱的高.
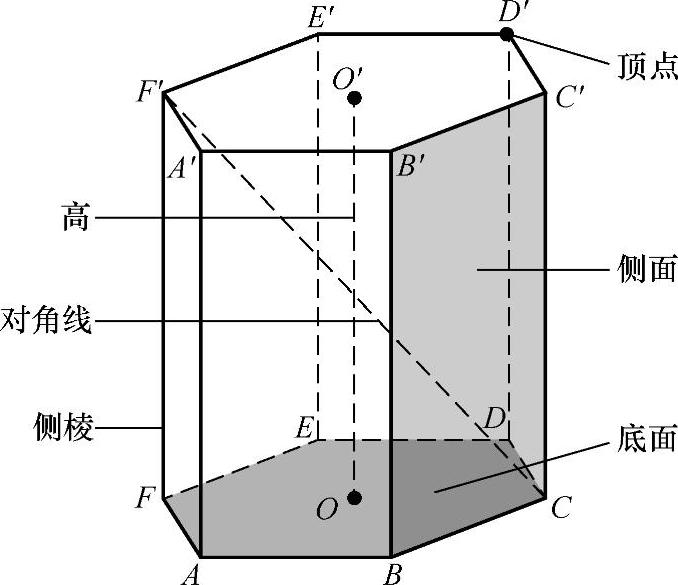
图3-26
棱柱通常用表示两个底面多边形的字母来表示,如图3-26所示的棱柱,可记作棱柱
ABCDEF-A′B′C′D′E′F′,或简单地用一条对角线的两个端点的字母来表示,如棱柱CF′.
侧棱不垂直于底面的棱柱叫做斜棱柱,如图3-27a所示;侧棱垂直于底面的棱柱叫做直棱柱,如图3-27b所示;底面是正多边形的直棱柱叫做正棱柱,如图3-27c所示.
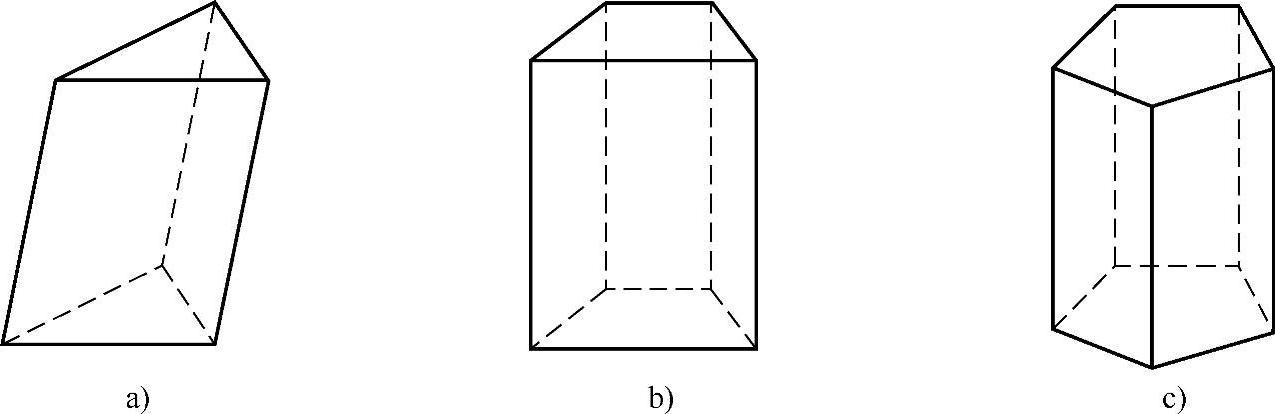
图3-27
棱柱的底面可以是三角形、四边形、五边形……这样的棱柱可以按照底面多边形的边数分别叫做三棱柱、四棱柱、五棱柱……(见图3-27)
(2)棱锥的结构特征
观察与思考
观察下面图片(见图3-28),说说图片中的几何体具有什么样的共同特征呢?

图3-28
它们都给人顶尖底平的、带棱的、锥体的印象.
一般地,有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面围成的多面体叫做棱锥(见图3-29).这个多边形叫做棱锥的底面(或底),其余各面叫做棱锥的侧面;相邻侧面的公共边叫做棱锥的侧棱;各侧面的公共顶点叫做棱锥的顶点;顶点到底面的距离叫做棱锥的高.
棱锥用表示顶点和底面各顶点,或者底面一条对角线端点的字母来表示.如图3-29所示的四棱锥可以表示为棱锥S-ABCD或S-AC.
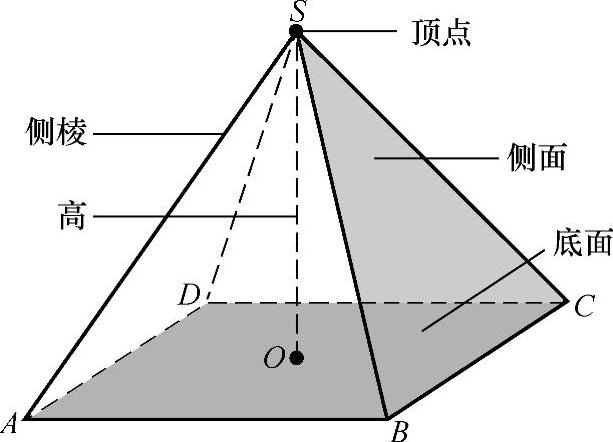
图3-29
底面是三角形、四边形、五边形、……的棱锥分别叫做三棱锥、四棱锥、五棱锥、……其中三棱锥又叫做四面体.
如果一个棱锥的底面是正多边形,并且顶点在底面上的投影是底面正多边形的中心,那么这样的棱锥叫做正棱锥.如图3-30a~c所示,它们分别为正三棱锥、正四棱锥和正六棱锥.
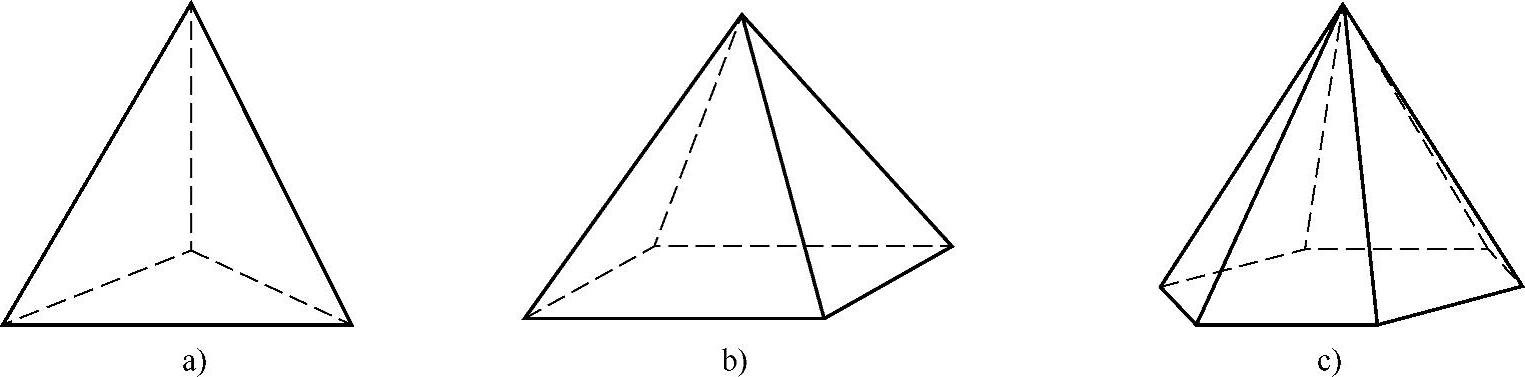
图3-30
正棱锥的各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形上的高相等,它叫做正棱锥的斜高.正棱锥的斜高相等.
侧棱的底面边长相等的正三棱锥叫做正四面体,如图3-30a所示.
练习
1.如习题图3-10所示,判断下面的多面体分别是几面体:
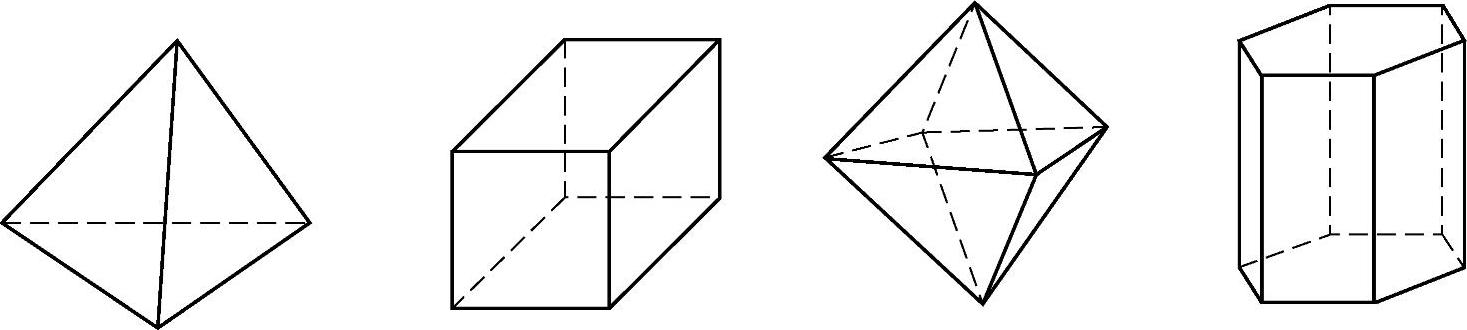
习题图3-10
2.用较厚的纸按照习题图3-11的样子分别画好并剪下,再把它折起来粘好,并说明得到的各几何体的名称.
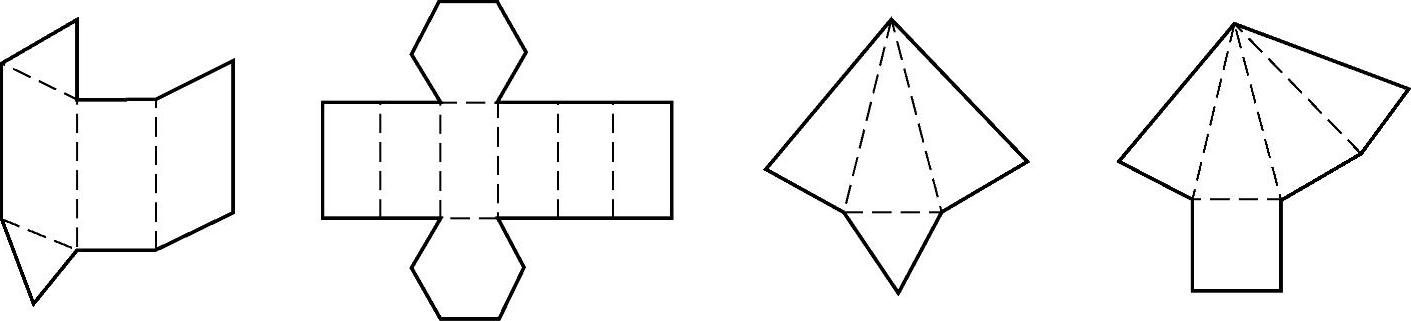
习题图3-11
3.判断下列命题是否正确:
(1)有两个面平行,其余各面都是四边形的几何体叫棱柱;( )
(2)正四棱柱是正方体;( )
(3)侧面都是等腰三角形的棱锥是正棱锥;( )
(4)有一个面是多边形,其余各面都是三角形的几何体叫棱锥;( )
(5)直棱柱的侧棱长与高相等.( )2.旋转体的结构特征
观察与思考
图3-31是在我们的生产和生活中常会出现的物体,观察它们的轮廓,可以抽象成什么样的几何体?它们又具有什么样的共同特征呢?
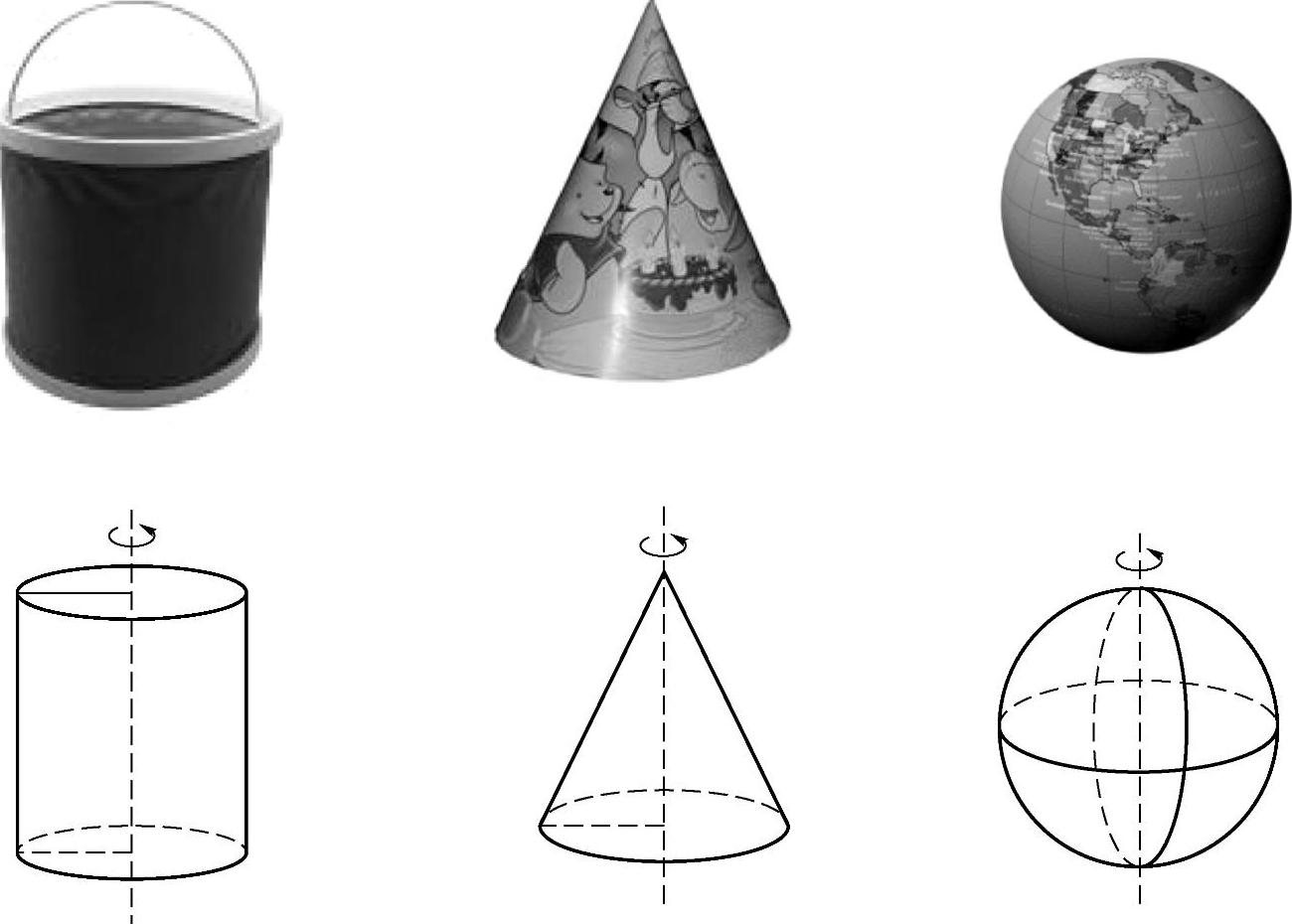
图3-31
这些物体抽象出的几何体都可以看成是由一个封闭的平面图形绕着它所在的平面内的一条定直线旋转一周所围成的,我们把这样的几何体叫做旋转体.这条定直线叫做旋转体的轴.
(1)圆柱结构特征
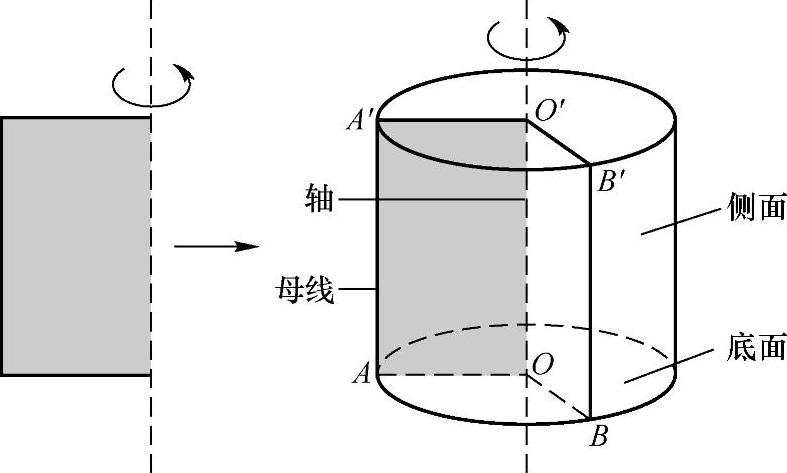
如图3-32所示,以矩形的一边所在直线为旋转轴,其余三边旋转形成的面所围成的旋转体叫做圆柱.旋转轴叫做圆柱的轴,垂直于轴的边旋转而成的圆面叫做圆柱的底面,平行于轴的边旋转而成的曲面叫做圆柱的侧面,无论旋转到什么位置,平行于轴的边都叫做圆柱的母线.
圆柱用表示它的轴的字母表示,如图3-32中的圆柱可表示为圆柱OO′.
圆柱和棱柱统称为柱体.
 (https://www.chuimin.cn)
(https://www.chuimin.cn)
图3-32
(2)圆锥的结构特征
与圆柱一样,圆锥也可以看做是由平面图形旋转而成的.
如图3-33所示,以直角三角形的一条直角边所在直线为旋转轴,其余两边旋转形成的面所围成的旋转体叫做圆锥.
圆锥也有轴、底面、侧面和母线.
圆锥和棱锥统称为锥体.
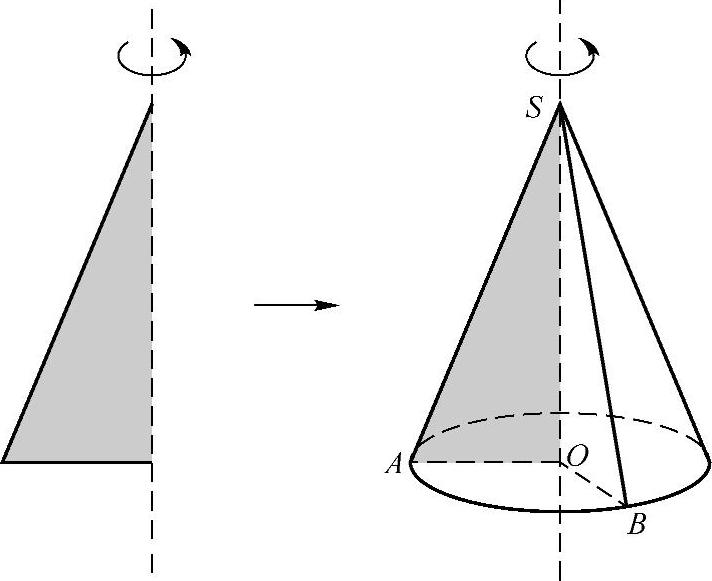
图3-33
试一试
请仿照圆柱中关于轴、底面、侧面及母线的定义,给出圆锥的轴、底面、侧面、母线的定义,并在图3-33中标注出来.
(3)球的结构特征
球是人们非常熟悉的几何体,如宇宙中的天体,体育比赛中的足球、篮球,还有机床中常用的滚珠等,都给我们留下球的印象.
球可以看做以半圆的直径所在的直线为旋转轴,半圆面旋转一周形成的旋转体,叫做球体(见图3-34),简称球.
半圆的圆心叫做球心,半圆的半径叫做球的半径,半圆的直径叫做球的直径.
球常用表示球心的字母来表示,如图3-35所示的球可以表示为球O.
可以发现,球面可以看做是一个半圆绕着它的直径所在的直线旋转一周所形成的曲面.
球面是到顶点(球心)的距离等于定长(半径)的所有点的集合.
球体是到定点(球心)的距离小于等于定长(半径)的所有点的集合.
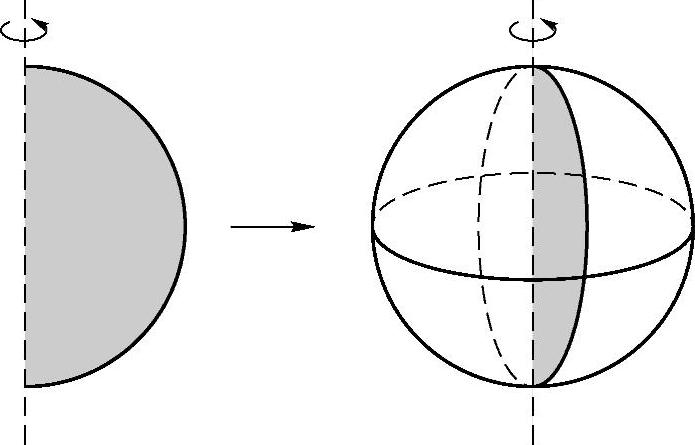
图3-34
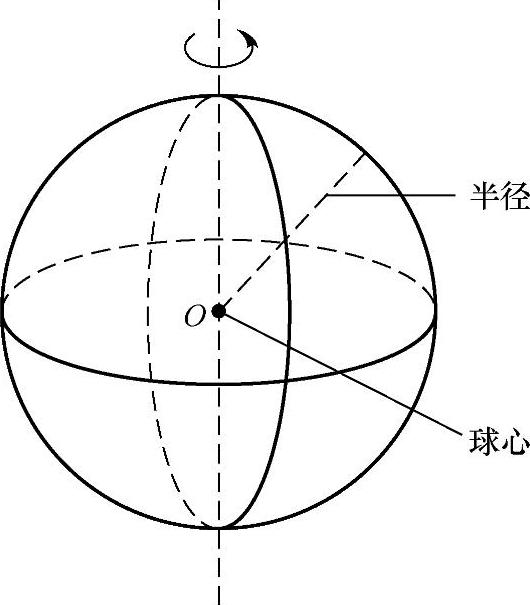
图3-35
练习
1.请举出日常生活中具有圆柱、圆锥、球体的形状的物体,并指出它们的结构特征.
2.判断题.
(1)以三角形的一条边所在的直线为旋转轴,其余两边旋转形成的面所围成的旋转体是圆锥;( )
(2)到定点的距离等于定长的所有点的集合是球面;( )
(3)经过球面上不同的两点只能做一个以球心为圆心的圆.( )
3.简单组合体的结构特征
我们观察现实世界中的物体,除了柱体、椎体和球体等基本几何体外,还有大量的几何体是由这些基本几何体组合而成的,这些几何体叫做简单组合体.图3-36所展示的是油泵的分解图,油泵可以看成是由一些基本几何体构成的简单几何体.对组合体可以通过把它们分解为一些基本几何体来研究.

图3-36
简单组合体的构成有两种基本形式:一种是由简单几何体拼接而成的(见图3-37);另一种则是由简单几何体截去或挖去一部分而成的(见图3-38).

图3-37

图3-38
试一试
请你指出图3-37、图3-38中的物体是由哪些简单几何体组合而成的.
练习
1.如习题图3-12所示,请指出下列物体的主要结构特征:

习题图3-12
2.如习题图3-13所示,将梯形ABCD绕AB所在直线旋转一周,由此形成的几何体是由哪些基本几何体构成的?你能画出图形吗?
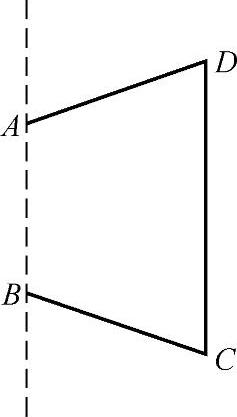
习题图3-13
习题二
1.选择题.
(1)如习题图3-14所示,下列几何体中不是棱柱的是( ).
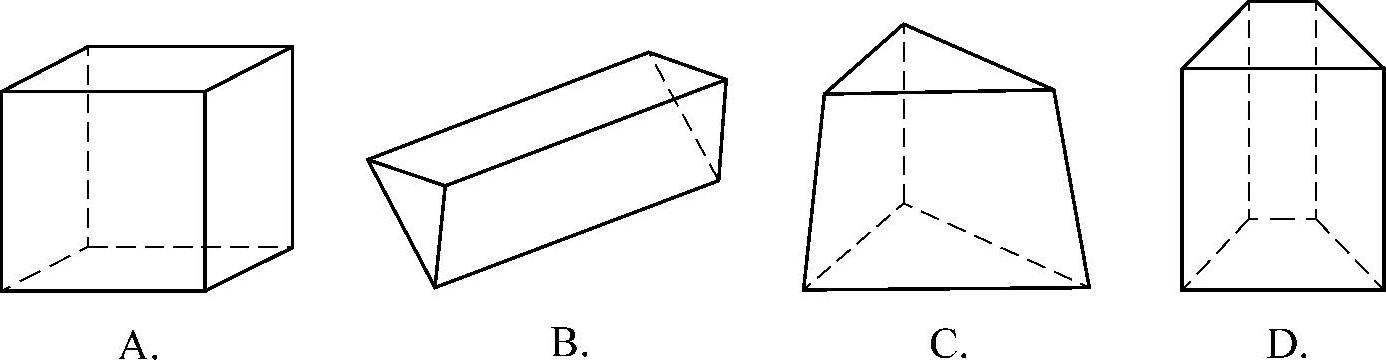
习题图3-14
(2)用任意一个平面去截一个几何体,各个截面都是圆面,则这个几何体一定是( ).
A.圆柱B.圆锥
C.球体D.圆柱、圆锥、球体的组合体
(3)将三角形绕直线旋转一周,可以得到如习题图3-15所示立体图的是( ).
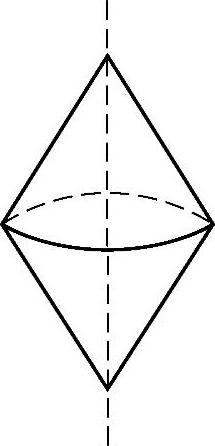
习题图3-15
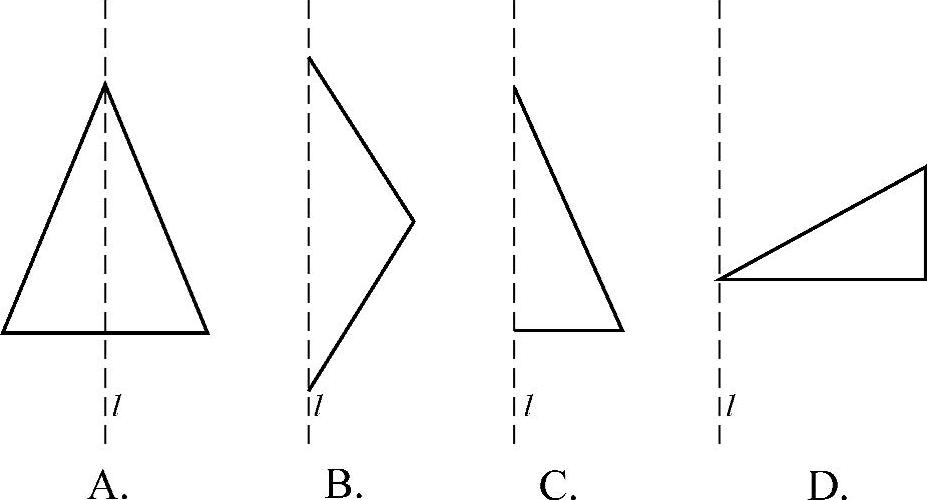
2.填空题.
(1)用符号“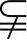 ”或“
”或“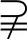 ”填空:
”填空:
①{正四棱柱}{直四棱柱};
②{长方体}{正方体};
③{正三棱锥}{三棱锥}.
(2)直棱柱的侧棱长与它的高,它的侧面形状是,经过不相邻的两条侧棱的截面形状是.
(3)侧棱垂直于底面的棱柱叫做,底面是正多边形的直棱柱叫做.
(4)以为旋转轴,旋转一周形成的旋转体叫做球体.
3.如习题图3-16所示,长方体ABCD-A′B′C′D′中被截去一部分,其中EH∥A′D′.剩下的几何体是什么?截去的几何体又是什么?你能说出它们的结构特征吗?
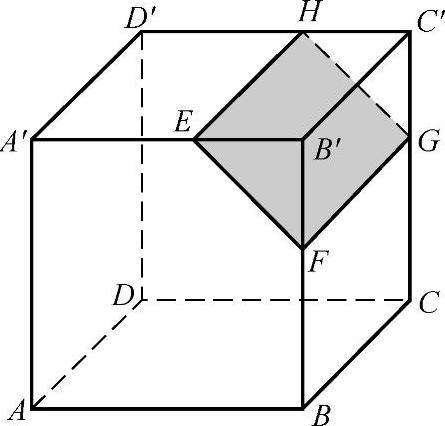
习题图3-16
相关文章

(一)相对性我们生活的周围空间是向纵、横、深三个方向扩展的,空间坐标系按照纵、横、深三个扩展方向形成的三对相对应的基本方向,分别表示为前后、左右和上下三对方向的位置。图10-2以小刚为参照物(三)连续性空间方位的连续性指的是空间方位从上到下、从前到后、从左到右等的区域是连续的,不能截然分开。可变性、相对性和连续性所反映的物体空间位置关系的基本特性是一致的。......
2025-09-29

回顾与思考初中学过的数,它们的关系可以归纳如下:议一议有理数和无理数有什么区别?数的集合简称数集,全体非负整数的集合,通常简称非负整数集,记作N,非负整数集内排除0的集合,也称正整数,记作N+;全体有理数的集合,简称有理数集,用Q表示;全体实数的集合,简称实数集,用R表示.为了方便,还用Q+表示正有理数集,Q-表示负有理数集;R+表示正实数集,R-表示负实数集.我们通常用大写拉丁字母A,B,C,…......
2025-09-30

由正弦函数y=sinx的图像可知:定义域正弦函数y=sinx的定义域是R.值域正弦函数y=sinx,x∈R的值域是[-1,1],即对任意的x∈R,都有-1≤sinx≤1.其中,当,k∈Z,有ymax=1;当,k∈Z时,有ymin=-1.想一想等式2sinx=3,,都成立吗?例2求出下列函数的最大值和最小值:y=1-sinx; y=2sinx.解:当sinx=-1时,ymax=1-(-1)=2;当sinx=1时,ymin=1-1=0.当sinx=1时,ymax=2×1=2;sinx=-1时,ymin=2×(-1)=-2.想一想第题中的函数y=1-sinx取得最大值和最小值时,对应的x的取值集合分别是什么?......
2025-09-30

1.任意角的三角函数的定义在本章的2.2节已经讨论了锐角的三角函数值,但是把角的概念推广以后,角可以为任意大小,那么对于任意角α,又该如何确定其三角函数值呢?......
2025-09-30

请你为剩下的那个图像写出与之相吻合的事件.习题图2-2我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;我骑着车一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间;我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.......
2025-09-30

习题七1.说明下列函数的图像是如何由函数y=sinx的图像变换得到的:2.已知电流I与时间t的关系式为I=Asinωt,其中,A=15,ω=100π.求电流I变化的周期和频率;当t=0s,,,,时,求电流I的值.......
2025-09-30

回顾与思考有理数加法法则:同号两数相加,取相同的符号,并把绝对值相加.异号两数相加,绝对值相等时和为0;绝对值不等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.一个数同0相加,仍得这个数.有理数减法法则:减去一个数,等于加上这个数的相反数.有理数乘法法则:两数相乘,同号得正,异号得负,绝对值相乘;任何数与0相乘,乘积仍为0.那么,在专业课学习中会遇到什么样的加减乘除运算呢?......
2025-09-30
相关推荐