请你为剩下的那个图像写出与之相吻合的事件.习题图2-2我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;我骑着车一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间;我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.......
2023-11-22
由正弦函数y=sinx的图像可知:
(1)定义域
正弦函数y=sinx的定义域是R.
(2)值域
正弦函数y=sinx,x∈R的值域是[-1,1],即对任意的x∈R,都有-1≤sinx≤1.
其中,当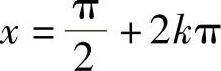 ,k∈Z,有ymax=1;当
,k∈Z,有ymax=1;当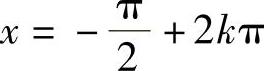 ,k∈Z时,有ymin=-1.
,k∈Z时,有ymin=-1.
想一想
等式2sinx=3, ,
,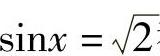
都成立吗?为什么?
例2 求出下列函数的最大值和最小值:
(1)y=1-sinx; (2)y=2sinx.
解:(1)当sinx=-1时,ymax=1-(-1)=2;
当sinx=1时,ymin=1-1=0.
(2)当sinx=1时,ymax=2×1=2;
sinx=-1时,ymin=2×(-1)=-2.
想一想
第(1)题中的函数y=1-sinx取得最大值和最小值时,对应的x的取值集合分别是什么?
工具箱“max”是英文maximum在数学中的缩写,是“最大值的”或“最大”的意思;“min”是英文minimum在数学中的缩写,是“最小值的”或“最小”的意思.
(3)周期性
一般地,对于函数y=f(x),如果存在一个不为零的常T,使得对于函数定义域内的任意x,等式f(x+T)=f(x)恒成立,那么称函数y=f(x)为周期函数.其中,常数T叫做该函数的周期.如果这样的常数T中存在一个最小的正数,那么这个最小的正数就叫做该函数的最小正周期.
观察函数y=sinx的图像,我们发现正弦函数的函数值按照一定的规律重复出现.这一点由公式sin(2kπ+x)=sinx(k∈Z)也可以得到证实.因此,正弦函数y=sinx是周期函数,它的周期不止一个,如2π,4π,6π等.
(4)奇偶性
观察正弦函数y=sinx,x∈R的图像,我们发现它的图像关于坐标原点对称.所以正弦函数y=sinx,x∈R是奇函数.
(5)单调性
观察正弦函数y=sinx,x∈R的图像可以看出:当x由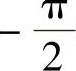
增大到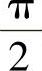
时,曲线逐渐上
升,即使sinx由-1增大到1;当x由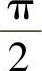
增大到
时,曲线逐渐下降,即sinx由1减少到
-1.具体变化如下表所示:
议一议
正弦函数有多少个单调区间?
例3 比较下列各组正弦值的大小:(www.chuimin.cn)
(1)
与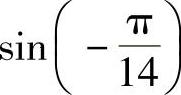 ;(2)
;(2)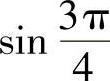
与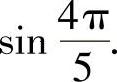
解:(1)因为 ,
, ,且
,且 ,
,
又因为y=sinx在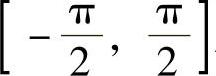
上是增函数;
所以 ;
;
(2)因为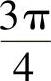 ,
, ,且
,且 ,
,
又因为y=sinx在
上是减函数,
所以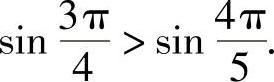
试一试
请利用计算器比一比上述各对正弦值的大小.
练习
1.求出下列函数的最大值和最小值:
(1)y=3+sinx; (2)y=-4sinx.
2.观察正弦曲线,写出满足下列条件的x的区间:
(1)sinx>0; (2)sinx<0.
3.利用正弦函数的单调性,比较下列各对正弦值的大小,并用计算器加以验证:
(1)sin190°与sin200°; (2)
与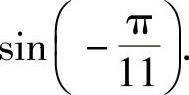
习题六
1.求下列函数的最大值和最小值:
(1)y=3-4sinx; (2)y=2sinx-1.
2.根据函数的单调性,比较下列各组中两个三角函数值的大小:
(1)sin112°与sin126°;(2)
与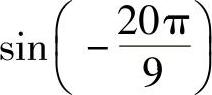 ;(3)
;(3)
sin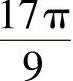
与
3.画出下列函数在[0,2π]上的简图:
(1)y=1-2sinx;
(2)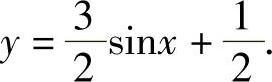
有关机电应用数学的文章

请你为剩下的那个图像写出与之相吻合的事件.习题图2-2我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;我骑着车一路匀速行驶,只是在途中遇到了一次交通堵塞,耽搁了一些时间;我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.......
2023-11-22

习题七1.说明下列函数的图像是如何由函数y=sinx的图像变换得到的:2.已知电流I与时间t的关系式为I=Asinωt,其中,A=15,ω=100π.求电流I变化的周期和频率;当t=0s,,,,时,求电流I的值.......
2023-11-22

这一节将介绍拉氏变换的几个基本性质,它们在拉氏变换的实际应用中都是很有用的.为了叙述方便,假定在这些性质中,凡是要取拉氏变换的函数都满足拉氏变换存在定理中的条件,并且把这些函数的增长指数统一地设为c.在证明这些性质时,不再重复这些条件.1.线性性质设α,β为常数,且则有或2.相似性质设a >0,若L[f(t)]=F (p),则类似有以上两条性质的证明与傅氏变换相应的性质的证明是一样的.3.微分性质......
2023-10-30

定义3 设α是任意一个复数,定义幂函数为w =zα =eαLnz(z 0).在α为正实数时,对z =0的情况进行规定:zα =0.幂函数是指数函数与对数函数的复合函数,根据对数函数的定义,有w =zα =eαLnz =eα(ln z+2kπi) =eα ln z·e2αkπi,(k为整数)由于Lnz = ln z+2kπi是多值的,所以w = zα也是多值的,且所取的不同数值的个数等于e2αkπi......
2023-10-30

解析函数是指在某个区域内可导的函数,它在理论和实际问题中应用广泛,具体定义如下:定义2 若函数f(z)在点z0的某个邻域内(包含点z0)处处可导,我们称f(z)在点z0处解析,也称它在z0全纯或正则,并称z0 是f(z) 的解析点,若函数f(z)在点z0处不解析,则称点z0 是f(z)的奇点; 若函数f(z)在区域D内的每一点都解析,则称函数f(z)在区域D内解析,或称f(z)是区域D内的解析函数......
2023-10-30

1.任意角的三角函数的定义在本章的2.2节已经讨论了锐角的三角函数值,但是把角的概念推广以后,角可以为任意大小,那么对于任意角α,又该如何确定其三角函数值呢?......
2023-11-22

探索直角三角形的边角关系直角三角形是我们生活中经常接触的图形,如果只知道直角三角形的一条边和一个锐角,你能求出其他的边和角吗?实例2:图2-5是两个自动扶梯,甲、乙两人分别从1号和2号自动扶梯上楼,谁先到达楼顶?练习1.在等腰三角形ABC中,AB=AC=5,BC=6,求sinB,cosB,tanB.2.在△ABC中,∠C=90°,,BC=20,求△ABC的周长.试一试两块不同的三角尺中有几个不同的锐角?......
2023-11-22
相关推荐