习题七1.说明下列函数的图像是如何由函数y=sinx的图像变换得到的：2.已知电流I与时间t的关系式为I=Asinωt，其中，A=15，ω=100π.求电流I变化的周期和频率；当t=0s，，，，时，求电流I的值.......
2023-11-22
利用描点法作出y=sinx函数图像
【摘要】：在一个圆周内，可以发现三角函数值具有“周而复始”的变化规律.三角函数的图像是如何反映这种变化规律的呢？下面利用“描点法”作出函数y=sinx，x∈[0，2π]的图像.列表描点连线用一条光滑的曲线把所描的点依次连接起来就画出了y=sinx，x∈[0，2π]的图像，如图2-19所示.图2-19因为终边相同的角的三角函数值相等，所以正弦函数y=sinx在x∈[-2π，0]，x∈[2π，4π]，x∈[4π，6π]，…
在一个圆周内，可以发现三角函数值具有“周而复始”的变化规律.三角函数的图像是如何反映这种变化规律的呢？
下面利用“描点法”作出函数y=sinx，x∈[0，2π]的图像.
（1）列表
（2）描点
（3）连线
用一条光滑的曲线把所描的点依次连接起来就画出了y=sinx，x∈[0，2π]的图像，如图2-19所示.
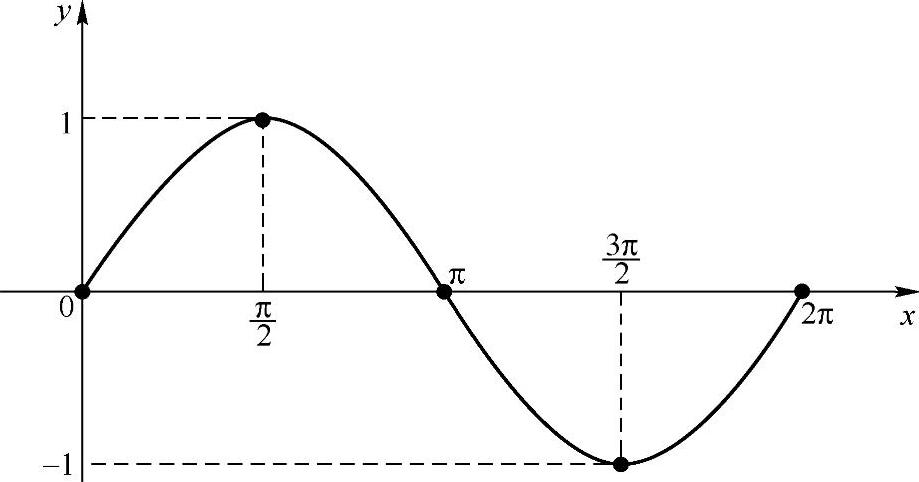
图2-19
因为终边相同的角的三角函数值相等，所以正弦函数y=sinx在x∈[-2π，0]，x∈[2π，4π]，x∈[4π，6π]，…时的图像，与x∈[0，2π]时的图像的形状完全一样，只是位置不同，因此只需把y=sinx，x∈[0，2π]的图像向左或向右平移2π，4π，…个单位，就可以得到正弦函数y=sinx，x∈R的图像，如图2-20所示.
图2-20
观察正弦函数y=sinx，x∈[0，2π]的图像.
不难看出，正弦函数图像中（0，0），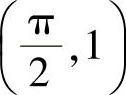
，（π，0），
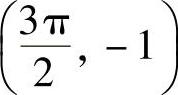，（2π，0）这5个点是确定正弦函数y=sinx，x∈[0，2π]图像的大致形状的关键点.就是说，把这5个关键点描出后，函数的大致图像就基本确定.因此，精确度不高时可以采用这种方法描出这5个关键点，然后用平滑的曲线连接起来，就得到相应区间上的正弦函数的简图.这种近似的画正弦函数简图的方法叫做“五点法”，这种方法简单易行.
例1 用“五点法”画出下列函数的简图：
（1）y=1+sinx，x∈[0，2π]； （2）y=-sinx，x∈[0，2π].(www.chuimin.cn)
解：（1）列表
描点画图，如图2-21中实线所示.
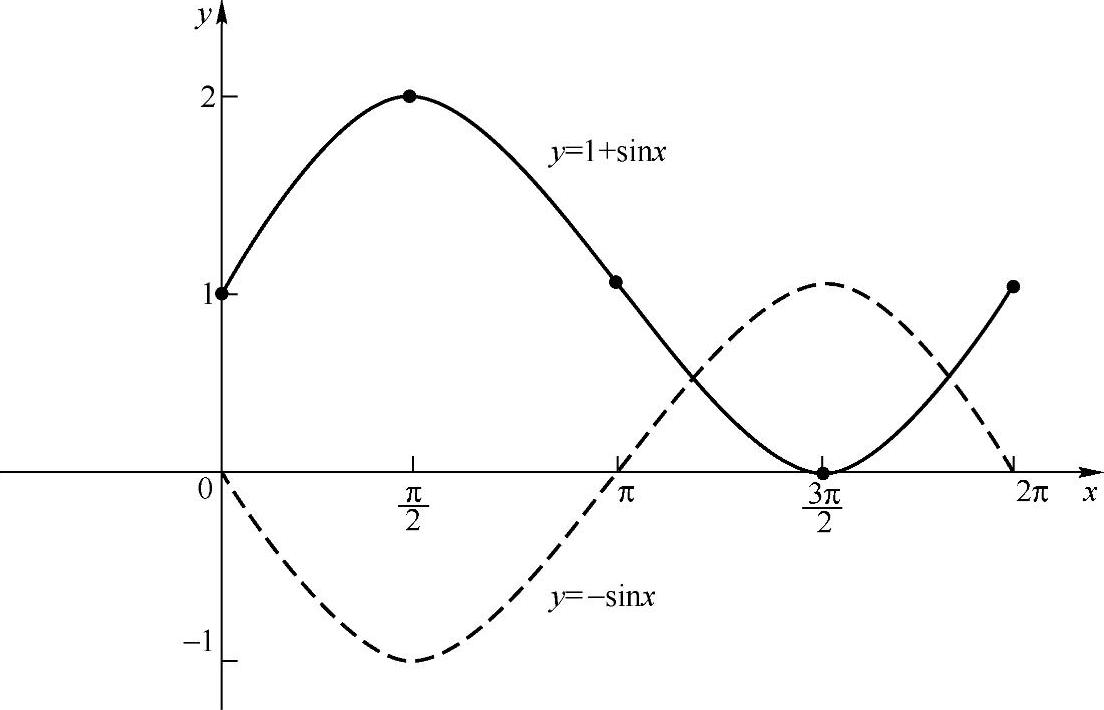
图2-21
（2）列表
描点画图，如图2-21中虚线所示.
议一议
观察图2-22，指出函数y=-sinx，x∈[0，2π]的图像（实线表示）与函数y=sinx，x∈[0，2π]的图像（虚线表示）之间的关系.
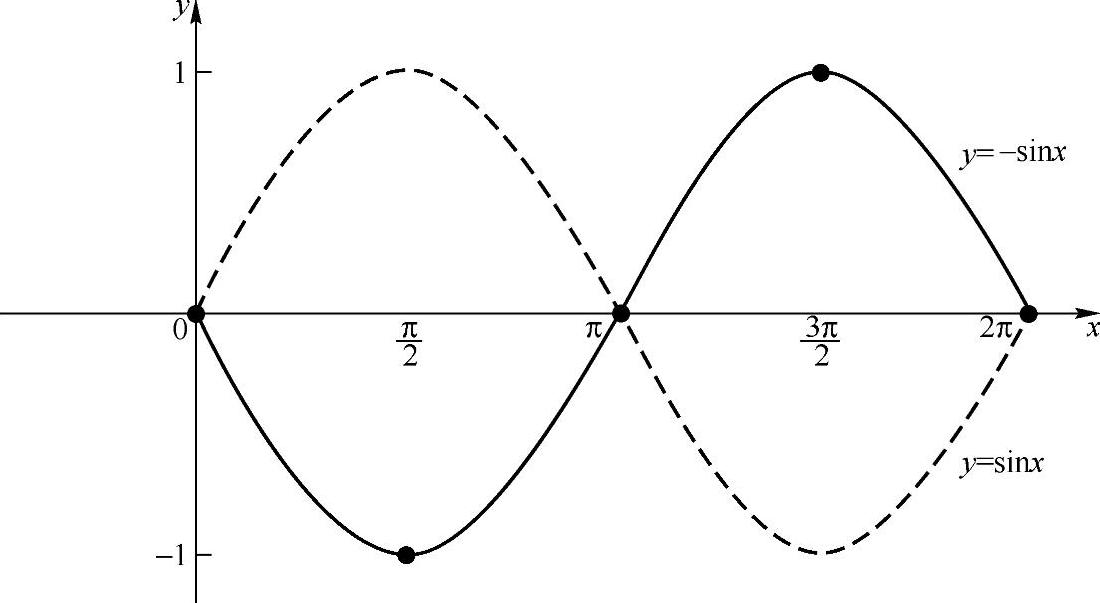
图2-22
练习
用“五点法”画出下列函数的简图：
（1）y=1-sinx，x∈[0，2π]； （2）y=2sinx-1，x∈[0，2π].
有关机电应用数学的文章
- 详细阅读
-
正切函数图像和性质的教学思考与实践详细阅读
问题1：你能结合所学的正切函数知识，类比正、余弦函数的性质，找出正切函数所具备的一些性质吗？如何用这些方法类比得出正切函数的图像？......
2023-07-31
-
图像内插实验：利用不同内插器对下取样图像进行详细阅读
利用上面介绍的16种内插器即理想、最近邻域、双线性、三次B样条、立方卷积、小波、全相位Ⅰ型，全相位Ⅱ型（共9种）对3幅2∶1下取样图像进行重构实验，其中全相位Ⅱ型除了行列方向使用一维模板分别进行内插恢复外，又可以设计二维模板直接内插重构，因此对应的内插方式共有27种。图8-30 测试图像及谱分布以woman.bmp为例，画出各种内插结果图，其中全相位Ⅱ型只画出了双窗结果。......
2023-06-23
-
高考必备：三角函数图像性质全解析详细阅读
续表考点：三角函数（2017全国I，9）已知曲线C1：y=cos x，C2：y=sin（2x+），则下面结论正确的是（）.A.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得曲线C2B.把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线C2C.把C1上各点的横坐标缩短到原来的，纵坐标不变，再把得到的曲线向右平移个单......
2023-10-15
-
二次函数y＝a（x－h）2＋k的图象和性质优详细阅读
一般地，抛物线y＝a（x－h）2＋k与y＝ax2形状________，位置_________，把抛物线y＝ax2向上（下）向左（右）平移，可以得到抛物线y＝a（xh）2＋k，平移的方向、距离要根据_________的值来决定．抛物线y＝a（x－h）2＋k有如下特点：（1）当a＞0时，开口________，当a＜0时，开口________；（2）对称轴是直线________；（3）顶点坐标是____......
2023-07-03
-
复合函数、反函数及隐函数导数计算详细阅读
【主要内容】计算函数的导数的基础是求导基本公式和四则运算法则.求导基本公式：（1）C′=0（C是常数），（2）（xμ）′=μxμ-1，（3）（ax）′=axlna（常数a>0但a≠1），特别地，（ex）′=ex，（4），特别地，，（5）（sinx）′=cosx， （6）（cosx）′=-sinx，（7）（tanx）′=sec2x， （8）（cotx）′=-csc2x，（9）（secx）′=secx......
2023-10-27
-
复变函数函数性态-复变函数及其应用详细阅读
如果是极点,指出它的级.解 令ζ = 则由于g(ζ)在ζ = 0解析且g 0,所以ζ = 0是的简单极点,因此z = ∞是f 的简单极点.......
2023-10-30
-
利用路西定理比较两个函数的零点个数详细阅读
利用路西(Rouche)定理,我们能对两个函数的零点的个数进行比较.设函数f(z)和g(z)在简单闭曲线C上和C内解析,且在C上满足条件|f(z)|＞|g(z)|,则在C上有|f(z)| ＞0,|f(z) + g(z)| ≥|f(z)| - |g(z)| ＞0.从而在C上f(z)和f(z)+g(z)都不等于零.又设N和N′分别为函数f(z)与f(z)+g(z)在C 的内部的零点个数.由于这两个函数......
2023-10-30
相关推荐