小学与初中散文教学内容的区别与衔接——以春酒为例叶晓峰作者简介:叶晓峰,浙江东阳人,杭州市上城区惠兴中学高级教师,主要从事中小学教育衔接研究与写作教学评价研究。并从恰当选择和确定中小学教学内容、比较准确地把握学情两个角度提出小学与初中散文教学内容衔接的建议。为此,我们利用九年一贯制的有利条件,探究小学、初中散文教学内容的区别与衔接。下面以春酒为例,阐述小学、初中散文教学的区别与衔接。......
2023-11-30
在初中阶段,我们学习过角的度量,具体做法是将一个周角分成360等分.规定其中的每一等分为1度(°)的角,这种以“度(°)”为单位来度量角的制度就叫做角度制.在角度制下,1周角=360°,1平角=180°,1直角=90°.
在数学和其他许多学科的研究中常常还应用到另一种度量角的制度——弧度制.弧度制就是以“弧度”为单位来度量角的制度.那么,弧度又是怎样的一种单位呢?
我们规定:在一个圆中,长度等于半径长的圆弧所对的圆的圆心角∠AOB就是1弧度的角.弧度记作rad.如图2-16所示,弧AB的长等于圆的半径r,那么弧AB所对的圆心角∠AOB就是1rad的角.又如图2-17所示,弧CD的长l=1.5r,那么,弧CD所对的圆心角∠COD就是1.5rad的角.
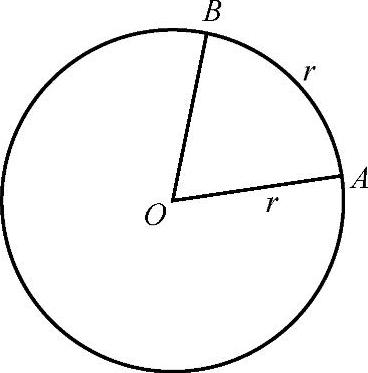
图2-16
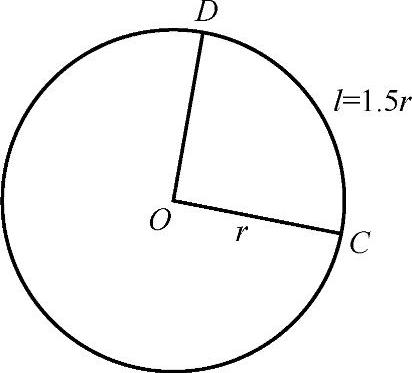
图2-17
建立了弧度制后,任何一个角都可以用弧度制和角度制来度量,同一个角的度数和弧度数是不同的(零角除外).
下面我们来研究弧度和度之间的换算关系.
一个周角等于360°,一个周角所对的弧长l=2πr(其中,r是圆的半径),就是一个圆周长,它的弧度数是

这就是说,一个周角等于360°,用弧度来度量它,等于2πrad,即360°=2πrad.因此得到弧度和角度的换算公式:
180°=πrad;
1弧度(1rad)≈57.3°;1°≈0.01745rad.
例1 分别将度(°)化成弧度(rad)、将弧度(rad)化成度(°).
(1)60°;
(2)
解:
(1)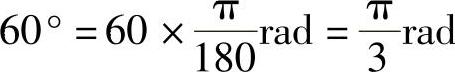 ;
;
工具箱
在角度制中,度、分、秒是60进制的,即1°=60′,1′=60″.
(2)
例2 按照下列要求,将67°30′化成弧度(rad):
(1)精确值;
(2)精确到0.001的近似值.
解:(1)
因为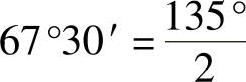 ,所以
,所以
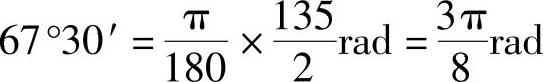
(2)利用计算器:(www.chuimin.cn)
第一步:将计算器先设置为线性状态,按键 ;
;
第二步:将单位设置为“弧度”,即Rad状态,按键 ;
;
第三步:将结果的精确度设置为小数点的后3位,按键
依次按键: ,
,
计算器显示

由于角有正角、负角和零角之分,我们规定:正角的弧度数为正数,负角的弧度数为负数,零角的弧度数为零,总之,任意一个角的弧度数是一个实数.于是,在弧度制下,角的集合和实数集R之间可以建立起这样的一种对应关系,即每一个角对应一个实数(即这个角的弧度数),不同的角对应不同的实数;反之,每一个实数对应一个角(即弧度数等于这个实数的角),不同的实数对应不同的角.如图2-18所示.
今后,如不产生混淆,用弧度作为单位表示角的大小时,“弧度”两字或“rad”可以省略不写.
例3 计算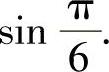
解:因为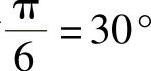 ,所以
,所以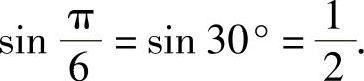
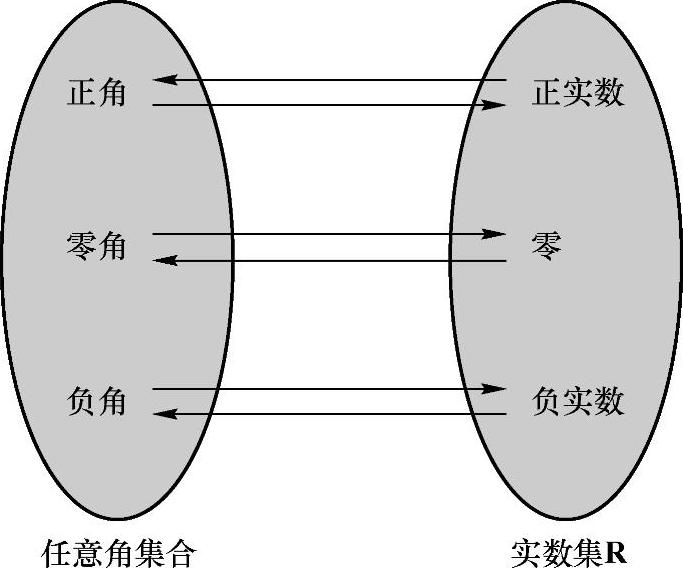
图2-18
练一练
计算: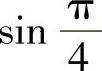 ,
,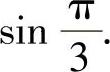
说明:对于特殊角,以两种单位度量,同学们应该可以直接写出它们的各种三角函数值.
练习
1.(口算)说出下列各度数分别对应的弧度数(用含π的式子表示):
(1)18°;(2)15°;(3)105°.
2.用计算器将下列各弧度化成度(精确到0.001):
(1)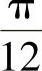 ;
;
(2)1.4.
习题五
1.将下列各度数化成弧度数(用含π的式子表示):
(1)12°;(2)390°;(3)-22.5°.
2.将下列各弧度数化成度数:

3.利用计算器将下列角度与弧度进行互化(精确到0.01):
(1)260°43′;(2) ;(3)410°15′;(4)(-6.7).
;(3)410°15′;(4)(-6.7).
有关机电应用数学的文章

小学与初中散文教学内容的区别与衔接——以春酒为例叶晓峰作者简介:叶晓峰,浙江东阳人,杭州市上城区惠兴中学高级教师,主要从事中小学教育衔接研究与写作教学评价研究。并从恰当选择和确定中小学教学内容、比较准确地把握学情两个角度提出小学与初中散文教学内容衔接的建议。为此,我们利用九年一贯制的有利条件,探究小学、初中散文教学内容的区别与衔接。下面以春酒为例,阐述小学、初中散文教学的区别与衔接。......
2023-11-30

极限偏差是相对于公称尺寸偏离大小的数值,即确定了极限尺寸相对公称尺寸的位置,它是限制实际偏差的变动范围。而公差仅表示极限尺寸变动范围的一个数值。......
2023-06-26

数字制造是实现智能制造的基础与手段,而智能制造是数字制造的提升。数字制造过程以信息处理为核心,而智能制造过程以智能学习与推理为核心。数字制造系统在环境异常或使用错误时无法正常工作,而智能制造系统则具有容错功能。......
2023-06-23

平陆大夫沉默片刻,说:是我孔距心的罪过。事情发生后,齐王很是后悔,说自己愧对孟子。当初周公派哥哥管叔监管殷商故国,管叔却率领殷人叛乱。陈贾面现得意,微笑道:看来圣人也会出现过错啊。犯了过错,耳根发热,心中羞愧,所谓“羞恶之心,人皆有之” ,这是人之常情,而陈贾反而大言不惭。按照孟子“无羞恶之心,非人也”的标准,陈贾做人不合格。......
2023-10-22

这种“不出资的对外直接投资”形态被称为业务控制。其实,业务控制并非合作经营,理由如下:中外双方并未组建合营实体,因此,不存在合作经营的载体。......
2024-04-02

从形式上看,带参数的宏调用和函数调用没有什么区别,而且确实在一些情况下它们产生同样的结果。例如:程序1:这两个程序的主函数main()是完全一样的,调用宏和调用函数得到相同的运行结果,都是5。理由是使用宏比函数调用更快。因为宏在真正编译之前已被相应地替换,在执行时,不必打断调用程序的运行,也没有参数的传递。......
2023-11-18

半精车的公差等级为IT10~IT9,表面粗糙度Ra为6.3~3.2 μm;精车的公差等级为IT8~IT7,表面粗糙度Ra为1.6~0.8 μm。在选择切削速度时,精车一般有高速精车和低速精车。......
2023-06-24

早在1993年,研究者就开始探讨有意走神和自发走神的差异。他们开发编制了MW-D和MW-S量表,分别测量这两个成分,信效度较好,被广泛使用。尽管有研究者认为任务完成过程中的MW是MW-S,但通过在实验任务中插入思维探测询问被试是否关注于任务,是有意MW还是无目的的MW,被试仍报告有34%~41%的MW是MW-D。而且,对完成任务持有低动机的个体,其MW-D比MW-S多。......
2023-11-20
相关推荐